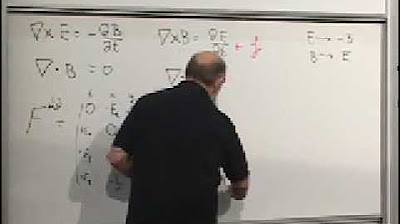15. Maxwell's Equations and Electromagnetic Waves II

YaleCourses

23 Mar 201169:29

EducationalLearning

32 Likes 10 Comments

TLDRIn this comprehensive lecture on electromagnetism, the professor delves into the intricacies of optics, quantum mechanics, and the fundamental concepts of complex numbers. He emphasizes the importance of understanding elementary calculus and the role of electric and magnetic fields in wave propagation. The lecture explores the mathematical representation of these fields, their visualization, and the physical meaning behind them. The professor clarifies the relationship between the wave number 'k', angular frequency 'ω', wavelength 'λ', and the velocity of light. He also discusses the concept of polarization and the conditions for the existence of electromagnetic waves in free space. The lecture further investigates the energy contained within these waves, introducing the Poynting vector to describe energy flux and intensity. The professor also touches on the historical context of special relativity and its impact on our understanding of electromagnetism, highlighting the revolutionary idea that the speed of light is constant for all observers. This thought-provoking lecture concludes with a challenge to the students to apply their knowledge to solve problems, reinforcing the significance of practice in grasping these complex topics.

Takeaways

📚 The final lecture on electromagnetism transitions into optics, which is considered a more concrete aspect of electromagnetism.
🌟 Understanding complex numbers, particularly e^(iθ), is fundamental before delving into quantum mechanics.
🧮 Basics of calculus, specifically with one variable, are essential for grasping the mathematics involved in electromagnetism.
🔍 Maxwell's equations in free space can be satisfied by any function for the electric and magnetic fields, leading to specific forms for E and B.
🌀 The electric and magnetic fields are transverse waves, oscillating in a plane perpendicular to the direction of propagation.
🌊 The wave nature of electromagnetic fields is demonstrated by their periodicity in space (wavelength λ) and time (周期 T).
📈 The energy density of an electromagnetic wave can be calculated and is found to be equal for both the electric and magnetic components.
🚀 Intensity (I), or the power per unit area, of an electromagnetic wave is determined by the Poynting vector, which is the cross product of the electric and magnetic fields.
🌞 Sunlight at the surface of the Earth has an intensity of about 1,000 watts per square meter, which corresponds to an average electric field of approximately 1,000 volts per meter.
🔋 Electromagnetic waves are produced by accelerating charges, as opposed to static charges or charges in uniform motion.
⚛️ The presence of magnetism can be deduced from electrostatics principles when considering relativistic effects, such as length contraction.

Q & A

What is the main topic of the final lecture?
-The main topic of the final lecture is electromagnetism, with a transition to optics and a brief mention of quantum mechanics.
Why is optics considered easier on the imagination compared to electromagnetism?
-Optics is considered easier on the imagination because it deals with more concrete things rather than abstract concepts, as is often the case with electromagnetism.
What mathematical concepts should students be familiar with before studying quantum mechanics?
-Students should be familiar with elementary complex numbers, such as understanding what e^(i)^(θ) represents, and basic calculus with just one variable.
What are the two conditions derived from the assumed form of E and B fields in a plane wave?
-The two conditions are that the angular frequency (ω) should be equal to k times the speed of light (c), and the magnetic field (B) should be equal to the electric field (E) divided by c.
What is the relationship between the wavelength (λ) and the wave number (k)?
-The wavelength (λ) is the reciprocal of the wave number (k), up to a factor of 2π, meaning that a larger k corresponds to a more rapidly oscillating wave with a shorter wavelength.
How is the time period (T) related to the angular frequency (ω)?
-The time period (T) is related to the angular frequency (ω) by the formula T = 2π/ω, which means that the time it takes for a wave to complete one full cycle is the inverse of the angular frequency multiplied by 2π.
What is meant by the polarization of a plane wave?
-Polarization refers to the direction of the electric field (E) in a plane wave. The magnetic field (B) is understood to be perpendicular to the electric field, and the direction of propagation is perpendicular to both E and B.
Why are electromagnetic waves considered transverse waves?
-Electromagnetic waves are considered transverse waves because the oscillations of the electric and magnetic fields are perpendicular to the direction of wave propagation.
What is the significance of the cross product E x B in terms of electromagnetic waves?
-The cross product E x B not only gives the direction of wave propagation but also represents the Poynting vector, which determines the rate at which energy is transferred across a unit area, or the intensity of the wave.
How can the average energy density of an electromagnetic wave be calculated?
-The average energy density of an electromagnetic wave can be calculated by taking half the product of the electric field energy density and the magnetic field energy density, which are equal due to their relationship through the speed of light (c).
What is the origin of electromagnetic waves?
-The origin of electromagnetic waves is accelerating charges. When charges in a system oscillate or accelerate, they generate time-varying electric and magnetic fields that can propagate as electromagnetic waves.

Outlines

00:00

📚 Final Lecture on Electromagnetism and Introduction to Optics

The professor begins the final electromagnetism lecture, reminding students that optics will follow, which is a part of electromagnetism but more concrete. The lecture emphasizes the importance of understanding complex numbers and calculus before delving into quantum mechanics. The professor also reviews how to solve Maxwell's equations in free space, discussing the conditions derived from the equations, such as the relationship between angular frequency and wave number with the speed of light, and the visualization of electric and magnetic fields.

05:01

🌉 Understanding Electromagnetic Waves and Their Properties

The summary explains the nature of electromagnetic waves, describing them as transverse waves where the electric and magnetic fields are perpendicular to the direction of wave propagation. The concept of polarization is introduced as the direction of the electric field, and it's noted that the magnetic field is perpendicular to it. The relationship between wavelength, wave number, and angular frequency is also discussed, along with the time and space dependence of the fields.

10:05

🌟 Energy in Electromagnetic Waves and Intensity of Light

This section delves into the energy contained within electromagnetic waves, discussing the energy density of both electric and magnetic fields and showing that they are equal. The average energy density is calculated, and the concept of intensity as the rate of energy transfer is introduced. The Poynting vector is explained as a way to determine the direction and magnitude of energy flow in electromagnetic waves, and an example of solar intensity reaching Earth is provided.

15:08

🌈 Polarization and the Superposition of Waves

The professor discusses the chaotic nature of light emitted by atoms, which is a superposition of plane waves with different polarizations. Plane waves are considered an idealization, as real light waves emanate spherically from a source. The polarization of light is related to the direction of the electric field, and the use of Polaroid lenses to control polarization is explained. The range of visible light is highlighted against the broader spectrum of electromagnetic waves.

20:11

🔋 Electromagnetic Field Generation and Energy Density

The origin of electromagnetic fields is explored, emphasizing that they are produced by accelerating charges. The scenario of an LC circuit with oscillating charges is provided as an example of how electromagnetic waves can be generated. The self-sustaining nature of electromagnetic fields is described, where changes in the electric field generate magnetic fields and vice versa, allowing the waves to propagate independently of the source.

25:13

🌌 The Implications of Special Relativity on Electromagnetism

The compatibility of Maxwell's equations with the principles of special relativity is discussed. It is highlighted that Maxwell's equations do not require a preferred frame of reference and are valid for all inertial observers. The constancy of the speed of light for all observers, regardless of their relative motion, is a cornerstone of special relativity and led to a revolution in physics, necessitating a new understanding of space and time.

30:15

🧲 Deduction of Magnetism from Electrostatics and Relativity

The professor demonstrates how magnetism can be deduced from electrostatics and the principles of special relativity. By considering a current-carrying wire and a stationary charge, and then analyzing the situation from the moving charge's frame of reference, it is shown that a magnetic force must act on the charge due to its velocity. This thought experiment illustrates the deep connection between electricity and magnetism and how they are revealed through the lens of relativity.

Mindmap

Keywords

💡Electromagnetism

Electromagnetism is a branch of physics that deals with the interaction between electric and magnetic fields. In the video, it is the main subject of the lecture, with the professor discussing various aspects such as Maxwell's equations, electromagnetic waves, and their properties.

💡Maxwell's Equations

Maxwell's equations are a set of four fundamental equations that describe the behavior of both electric and magnetic fields, as well as their interactions with matter. The professor refers to these equations as the foundation for understanding how any function satisfying them can describe electromagnetic waves in free space.

💡Polarization

Polarization refers to the direction of the electric field vector in an electromagnetic wave. It dictates the orientation of the wave and is a key concept in the study of wave behavior, as discussed by the professor when explaining how the direction of the electric field (E) affects the propagation of the wave.

💡Wavelength

The wavelength (λ) is the distance between two consecutive points in a wave that are in the same phase. The professor uses the concept of wavelength to explain the relationship between the wave number (k) and the frequency of the wave, noting that the wavelength is the reciprocal of the wave number multiplied by 2π.

💡Wave Number

The wave number (k) is a measure of the number of wavelengths per unit distance, and it is related to the spatial frequency of the wave. The script mentions that a larger wave number corresponds to a more rapidly oscillating wave, which means a shorter wavelength.

💡Angular Frequency

Angular frequency (ω) is a measure of how fast an oscillation changes with time, and it is related to the frequency of the wave. The professor clarifies that angular frequency ω is 2π times the frequency, which is the number of cycles per second that a wave completes.

💡Transverse Wave

A transverse wave is a type of wave, such as light or electromagnetic waves, where the displacement of the medium is perpendicular to the direction of the wave's propagation. The professor explains that electromagnetic waves are transverse, with both the electric and magnetic fields oscillating perpendicular to the direction of wave travel.

💡Poynting Vector

The Poynting vector is a quantity that represents the directional energy flux (the rate of energy transfer) in an electromagnetic field. The professor introduces the Poynting vector as E x B over μ_0, where E is the electric field, B is the magnetic field, and μ_0 is the permeability of free space, and explains that its magnitude gives the intensity of the electromagnetic wave.

💡Intensity

Intensity (I) of an electromagnetic wave is the power transferred per unit area, typically measured in watts per square meter. The professor calculates the intensity by multiplying the energy density by the velocity of light, showing how it gives the rate at which energy is transferred past a given point.

💡Relativity

Relativity refers to the physical theory developed by Albert Einstein, which describes the behavior of objects in high-velocity motion relative to an observer. The professor touches on the concept by discussing how Maxwell's equations, which underpin electromagnetism, are consistent with the principles of special relativity, leading to the understanding that the speed of light is constant for all observers.

💡Electromagnetic Waves

Electromagnetic waves are waves that consist of oscillating electric and magnetic fields that propagate through space. The professor discusses the properties of these waves, including their polarization, wavelength, frequency, and how they are generated by accelerating charges, which is a fundamental concept in electromagnetism.

Highlights

Introduction to the final lecture on electromagnetism and the transition to optics.

The importance of understanding complex numbers and elementary calculus in the study of electromagnetism.

Explanation of how to solve Maxwell's equations in free space using any function for E and B that satisfies the equations.

Derivation of the conditions that ω should equal k times c and the magnetic field should be the electric field divided by c.

Visualization of electric and magnetic fields and their physical interpretation.

The relationship between the wave number (k), angular frequency (ω), wavelength (λ), and the time period (T).

Description of the polarization of electromagnetic waves and its significance.

The concept of transverse waves in contrast to longitudinal waves, with examples provided.

The significance of the cross product E x B in determining the direction of wave propagation.

Discussion on the energy contained in an electromagnetic wave and the concept of energy density.

Calculation of the average energy density and the concept of intensity as it relates to the flow of energy.

Explanation of the Poynting vector and its role in determining the flux of energy in electromagnetic waves.

The impact of special relativity on the understanding of electromagnetism and the constancy of the speed of light for all observers.

Derivation of the presence of magnetism based on the principles of relativity and electrostatics.

Discussion on the transformation of velocities in the context of special relativity and its implications for the addition of velocities.

The deduction of the magnetic force experienced by a moving charge due to a current-carrying wire, purely from the perspective of electrostatics and relativity.

Recommendation for students to practice problems during the break to solidify their understanding of the concepts discussed.

Transcripts

Browse More Related Video

19. Waves

Lectures 2 & 3 | Quantum Entanglements, Part 3 (Stanford)

Sound Waves and the Acoustic Spectrum | Ultrasound Physics | Radiology Physics Course #1

Special Relativity | Lecture 1

18. Wave Theory of Light

01 - Oscillations And Simple Harmonic Motion, Part 1 (Physics Tutor)

Related Tags

Electromagnetism Optics Quantum Mechanics Special Relativity Electromagnetic Waves Light Polarization Poynting Vector Energy Density Maxwell's Equations Transverse Waves Lecture Series