Simple Harmonic Motion: Hooke's Law

Professor Dave Explains
10 Mar 201704:49
EducationalLearning
32 Likes 10 Comments

TLDRIn this informative discussion, Professor Dave delves into the concept of simple harmonic motion, a type of periodic motion exemplified by a mass-spring system. He explains the interplay between kinetic and potential energy, the sinusoidal graph of the block's position over time, and the role of Hooke's law in describing the spring's restoring force. The video also touches on the impact of friction and the uniqueness of each spring's spring constant, k, which dictates the system's behavior. Understanding these principles is crucial for grasping the physical phenomena of oscillations.

Takeaways
  • 📈 Simple harmonic motion is a type of periodic motion, like a pendulum or a spring vibrating back and forth.
  • 📊 In an ideal mass-spring system, a block attached to a spring oscillates between compressed and less compressed states in a frictionless environment.
  • 📐 The graph of the block's position over time shows sinusoidal behavior, similar to a sine function, with the block returning to the same positions periodically.
  • 🎢 At the equilibrium position (x=0), the block is in its original state before being disturbed, and it oscillates between positive and negative x values indefinitely in a frictionless scenario.
  • 🔢 Frictional forces in reality will cause the spring's activity to dampen over time, eventually stopping the motion.
  • 🔧 The spring constant (k) represents the unique stiffness of a spring, with loose springs like a slinky having a lower k value and stiff springs having a higher k value.
  • 📐 Hooke's law states that the force exerted by a spring is equal to -k times the displacement of the object, with the negative sign indicating the force is always opposite the direction of the object's movement.
  • 🔄 The spring's restoring force attempts to move the object back to its equilibrium position, which is why the force is called a restoring force.
  • ⚖️ The units of the spring constant are Newtons per meter (N/m), and when multiplied by displacement (x), it gives the force needed to compress or stretch the spring by that distance.
  • 🔋 The elastic potential energy of a spring is given by (1/2)kx^2, where k is the spring constant and x is the distance the spring is stretched or compressed from its equilibrium position.
  • 🔄 Kinetic and elastic potential energies interchange as the mass oscillates, with the maximum potential energy occurring at the maximum distance from the equilibrium position during the oscillation.
Q & A

  • What is simple harmonic motion?

    -Simple harmonic motion is a type of periodic motion where an object moves back and forth along a straight line, such as a pendulum swinging or a spring vibrating. The motion is characterized by the object's acceleration being proportional to its displacement and acting in the opposite direction.

  • What are the key characteristics of an ideal mass-spring system?

    -In an ideal mass-spring system, the surface of motion is assumed to be completely frictionless, allowing the mass to oscillate indefinitely between compressed and less compressed states without losing energy. The system is described by Hooke's law, where the force exerted by the spring is proportional and opposite to the displacement of the mass.

  • How does friction affect the motion of a spring in a real-world scenario?

    -Frictional forces dampen the spring's activity, causing the oscillations to gradually lose energy and eventually come to a stop. This is different from an ideal mass-spring system, which assumes no friction and thus the mass would oscillate indefinitely.

  • What is Hooke's law and how is it represented mathematically?

    -Hooke's law states that the force exerted by a spring is equal to the negative product of the spring constant (k) and the displacement (x) of the object it acts upon. Mathematically, it is represented as F = -kx, where the negative sign indicates that the force of the spring is always in the opposite direction of the object's movement.

  • What is the restoring force in the context of a mass-spring system?

    -The restoring force is the force exerted by the spring that attempts to move the object back to its equilibrium position. It is a result of the spring's tendency to resist deformation and is directed opposite to the displacement of the mass from its equilibrium position.

  • How does the elastic potential energy of a spring change during its oscillation?

    -The elastic potential energy of a spring is maximum when the spring is most compressed or least compressed (at the extremes of its oscillation) and is minimum when the spring is at its equilibrium position. The formula for elastic potential energy is U = (1/2)kx^2, where k is the spring constant and x is the displacement from the equilibrium position.

  • What is the relationship between the elastic potential energy and kinetic energy in a mass-spring system?

    -In a mass-spring system, the elastic potential energy and kinetic energy interchange as the mass oscillates. At the maximum compression or extension, the kinetic energy is zero and the potential energy is at its maximum. Conversely, at the equilibrium position, the potential energy is zero and the kinetic energy is at its maximum.

  • What is the significance of the spring constant (k) in Hooke's law?

    -The spring constant (k) represents the stiffness of the spring. It is unique to each spring and determines the amount of force needed to compress or extend the spring by a certain distance. The units of k are Newtons per meter (N/m), and it dictates the relationship between the force exerted by the spring and the displacement of the object it acts upon.

  • How does the motion of a pendulum relate to simple harmonic motion?

    -A pendulum exhibits simple harmonic motion as it swings back and forth under the influence of gravity. Although the energy involved is gravitational potential energy rather than elastic potential energy, the motion is similar to that of a mass-spring system, with the pendulum swinging between two positions and undergoing periodic oscillations.

  • What would be the graph of a mass-spring system's position versus time?

    -The graph of a mass-spring system's position versus time would display sinusoidal behavior, similar to a trigonometric sine function. This reflects the periodic nature of the motion, with the mass oscillating between positive and negative displacements from its equilibrium position over time.

  • How does the concept of simple harmonic motion apply to real-world objects like a Slinky or a pinball spring?

    -Simple harmonic motion can be observed in real-world objects like Slinkies and pinball springs, although each spring has a unique spring constant (k) that determines its stiffness. The motion of these objects can be approximated by an ideal mass-spring system, which helps in understanding and predicting their behavior under various conditions.

Outlines
00:00
📚 Introduction to Simple Harmonic Motion

Professor Dave introduces the concept of simple harmonic motion, distinguishing it from non-periodic motion like a rock falling from a cliff. He explains that simple harmonic motion involves periodic, repeated movements, such as a pendulum swinging or a spring vibrating. The lecture focuses on a theoretical mass-spring system, where a block attached to a spring oscillates between compressed and less compressed states. The motion is described as sinusoidal and the block's movement is graphed against time. The concept of equilibrium position is introduced, with x=0 marking this point. The influence of friction on real-world systems is acknowledged, and the spring constant k is defined, relating to Hooke's law. The force exerted by the spring is a restoring force, always opposite to the object's movement direction. The units for the spring constant are Newtons per meter, and the elastic potential energy is calculated as half k times x squared.

Mindmap
Keywords
💡Simple Harmonic Motion
Simple harmonic motion refers to the periodic, oscillatory movement of an object where the restoring force is directly proportional to the displacement and in the opposite direction. In the video, this concept is illustrated by the example of a mass attached to a spring, which vibrates back and forth between compressed and less compressed states. The motion is periodic, meaning it repeats itself over time, and is represented graphically by a sinusoidal wave, similar to a sine function.
💡Elastic Potential Energy
Elastic potential energy is the potential energy stored in an object when it is stretched or compressed. In the context of the video, when a spring is either compressed or expanded, it stores elastic potential energy. The amount of energy stored is proportional to one-half the spring constant (k) times the square of the displacement (x). This energy is at a maximum when the spring is most compressed or least compressed, and it decreases as the spring moves towards its equilibrium position.
💡Hooke's Law
Hooke's Law describes the relationship between the force exerted by a spring and the displacement of the object it acts upon. According to the law, the force (F) is equal to the negative of the spring constant (k) times the displacement (x), expressed as F = -kx. The negative sign indicates that the force exerted by the spring is always in the opposite direction to the displacement, meaning the spring always attempts to restore itself to its equilibrium position.
💡Kinetic Energy
Kinetic energy is the energy of motion possessed by an object. In the video, kinetic energy is discussed in relation to the mass oscillating on a spring. As the mass moves towards the equilibrium position, it gains kinetic energy, reaching a maximum when it passes through the equilibrium point, moving the fastest.
💡Spring Constant (k)
The spring constant, denoted as k, is a measure of a spring's stiffness. It determines the amount of force needed to compress or extend the spring by a given distance. In the video, it is explained that different springs have different spring constants, which can be loose like a slinky or stiff like the spring in a pinball machine. The units for the spring constant are Newtons per meter (N/m), indicating the force in Newtons required to stretch or compress the spring by one meter.
💡Restoring Force
A restoring force is the force that brings an object back to its equilibrium position. In the context of the video, the force exerted by the spring is a restoring force because it always acts to return the mass to the center of its oscillation. This force is a key component of simple harmonic motion, as it is what allows the object to oscillate back and forth.
💡Damping
Damping refers to the reduction of amplitude in oscillations due to the presence of resistive forces, such as friction or air resistance. In the video, it is mentioned that in reality, frictional forces will dampen the spring's activity, causing the oscillations to decrease in amplitude over time until the system eventually comes to a stop.
💡Frictionless Motion
Frictionless motion is an idealized concept where an object moves without any resistance. In the video, the assumption of a frictionless surface allows for the idealized model of simple harmonic motion to be discussed, where the block on the spring would oscillate indefinitely without losing energy.
💡Sinusoidal Behavior
Sinusoidal behavior describes a pattern of oscillation or vibration that follows the shape of a sine wave. In the video, the motion of the block attached to the spring is described as sinusoidal because it oscillates back and forth in a repeating pattern that can be graphed as a sine function.
💡Periodic Motion
Periodic motion is a type of motion that repeats at regular intervals. In the video, simple harmonic motion is characterized as periodic because the object (like the block on the spring) returns to the same position at regular time intervals, continuing this cycle indefinitely under ideal conditions.
💡Equilibrium Position
The equilibrium position is the position where the net force on an object is zero, and it is typically the position of rest or balance. In the context of the video, the equilibrium position of the block on the spring is where it was before it was pulled. At this point, the spring is neither compressed nor expanded, and the block has no net force acting on it, allowing it to oscillate back and forth around this position.
Highlights

Definition of simple harmonic motion as periodic motion, such as pendulum or spring vibration.

Description of a mass-spring system as an example of simple harmonic motion.

Explanation of how a spring's elastic potential energy and kinetic energy interchange during oscillation.

The role of friction in damping the spring's activity and eventually stopping the oscillation.

Variability in spring constants (k) representing the stiffness or looseness of different springs.

Hooke's law as the relationship between the force a spring can exert and the displacement of the object.

The negative sign in Hooke's law indicating the force's direction opposite to the object's movement.

The spring's restoring force aiming to return the object to its equilibrium position.

Units of the spring constant (Newtons per meter) and its calculation based on displacement.

Elastic potential energy formula (1/2 kx^2) and its relation to the spring's stretched or compressed distance.

Comparison of elastic potential energy and kinetic energy expressions, highlighting their interchangeability.

Introduction to pendulum motion as another example of periodic motion involving gravitational potential energy.

The sinusoidal behavior of the mass-spring system, graphed as a sine wave against time.

Infinite oscillation between positive and negative x in a frictionless environment.

Equilibrium position of the block at x equals 0 and its significance.

The practical approximation of real-world systems with an ideal mass-spring system.

The transition from potential to kinetic energy as the mass oscillates in the spring system.

The comprehensive tutorial on simple harmonic motion and its applications.

Transcripts

Browse More Related Video

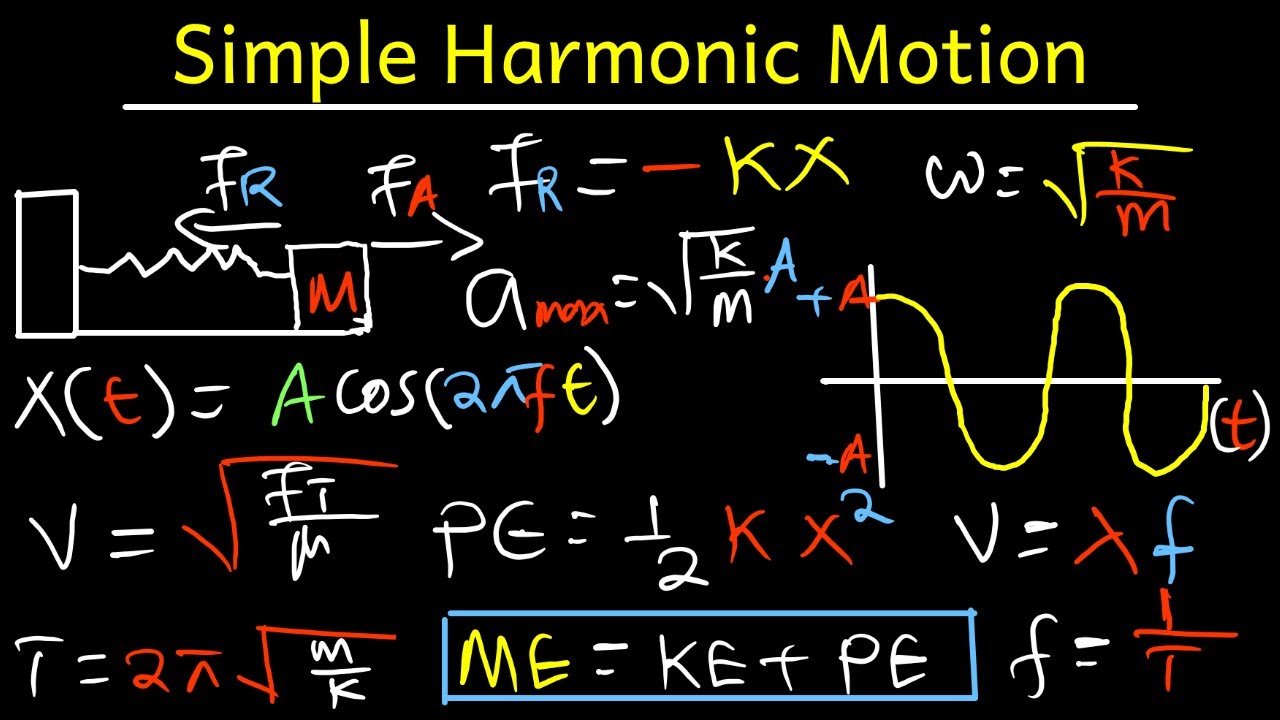
Simple Harmonic Motion, Mass Spring System - Physics Full Topic

17. Simple Harmonic Motion

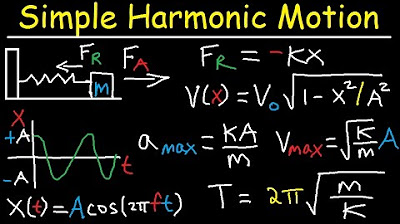
Simple Harmonic Motion, Mass Spring System - Amplitude, Frequency, Velocity - Physics Problems

Simple Harmonic Motion - Complete Review of the Mass-Spring System

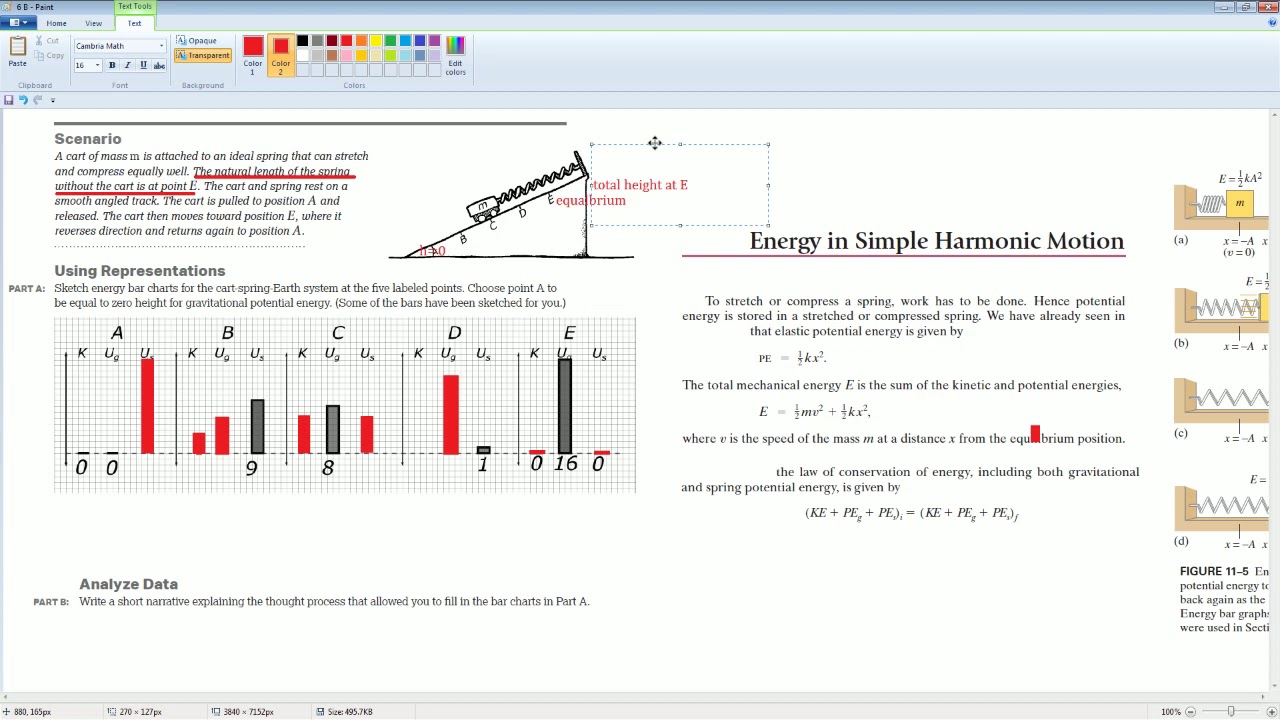
AP Physics Workbook 6.B Simple Harmonic Motion and Energy Review

Hooke's Law and Elastic Potential Energy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics TutorialSimple Harmonic MotionSpring ConstantHooke's LawElastic Potential EnergyKinetic EnergyMass-Spring SystemPendulum MotionRestoring ForceEnergy Interchange