4. Newton's Laws (cont.) and Inclined Planes
TLDRThe provided transcript is a detailed physics lecture that delves into the application of Newton's laws of motion, particularly focusing on problems involving forces and motion in various contexts such as springs, inclined planes, and circular motion. The lecturer emphasizes the importance of understanding the principles behind these laws and their practical applications, such as calculating the force exerted by a spring, analyzing the conditions for an object to start sliding down an inclined plane, and understanding the dynamics of a car taking a turn or an object in circular motion. The lecture also touches on the concept of friction and its role in real-world scenarios, including the banking of roads and the design of amusement park rides. The summary of the lecture would highlight the interactive nature of the session, the practical examples used to explain complex concepts, and the emphasis on critical thinking and problem-solving skills in physics.
Takeaways
- 🎓 **Engagement in Classroom**: The professor emphasizes the importance of a small class size for dialogue and interaction, although it's not possible in an introductory course, the professor still encourages students to ask questions and discuss related issues.
- 🤔 **Importance of Questions**: The professor highlights that student questions and viewpoints can be surprising and lead to interesting discussions, even on well-known subjects for the professor.
- 📚 **Application of Newton's Laws**: The use of physical laws, particularly Newton's laws, is to predict future events based on current information, which is demonstrated through a spring-mass system example.
- 🔍 **Understanding Forces**: The professor explains that to use Newton's laws, one must know the forces acting on a body, which requires understanding the nature of the force, not just the mathematical formula.
- 📐 **Differential Equations**: The concept of differential equations is introduced as a way to express and solve problems involving unknown functions and their derivatives.
- 🧮 **Guessing Solutions**: Solving differential equations often involves guessing solutions that fit the equation, which is a common method in physics.
- 🔄 **Oscillation Problem**: A detailed example of a mass attached to a spring is used to illustrate how to apply Newton's laws and solve for the motion of the system over time.
- 🚗 **Friction and Newton's Laws**: The role of friction as a force that opposes motion is discussed, and how it must be accounted for in the application of Newton's laws.
- 🌐 **Limits of Newton's Laws**: The professor discusses the limitations of Newton's laws, such as their inapplicability at speeds close to light or at the quantum scale, and introduces the concept of domains of validity for physical laws.
- 🔍 **Observation and Theory**: The iterative process of physics is emphasized, where observations lead to the identification of forces, which then must be integrated into existing theories, and new theories are developed when existing ones fail.
- 📈 **Vectors in Physics**: The treatment of forces and acceleration as vectors is explained, with examples of how to resolve forces along different axes and how this is applied to problems like those involving inclined planes.
Q & A
What is the main challenge in applying Newton's laws to real-world scenarios?
-The main challenge is identifying all the forces acting on a body. If all forces are not accounted for, the application of Newton's laws may not yield accurate results.
Why is it important to work with symbols rather than numbers until the end of a physics problem?
-Working with symbols allows for greater flexibility and understanding of the underlying principles. It also makes it easier to adjust for different values of variables without recalculating the entire problem.
What is the role of friction in the motion of objects?
-Friction opposes the motion of objects. It can prevent an object from moving when the applied force is less than the maximum static friction, and once movement begins, it provides a force opposite to the direction of motion, known as kinetic friction.
How does the banking of a road help in a vehicle's turn without relying on friction?
-Banking a road at an angle allows the normal force exerted by the road to have a horizontal component that points towards the center of the circular path. This helps in turning the vehicle without the need for friction.
What is the minimum speed required for a vehicle to successfully navigate a loop-the-loop without falling down?
-The minimum speed required is such that the square of the velocity (v²) is greater than or equal to the product of the radius (R) and the acceleration due to gravity (g), i.e., v² ≥ Rg.
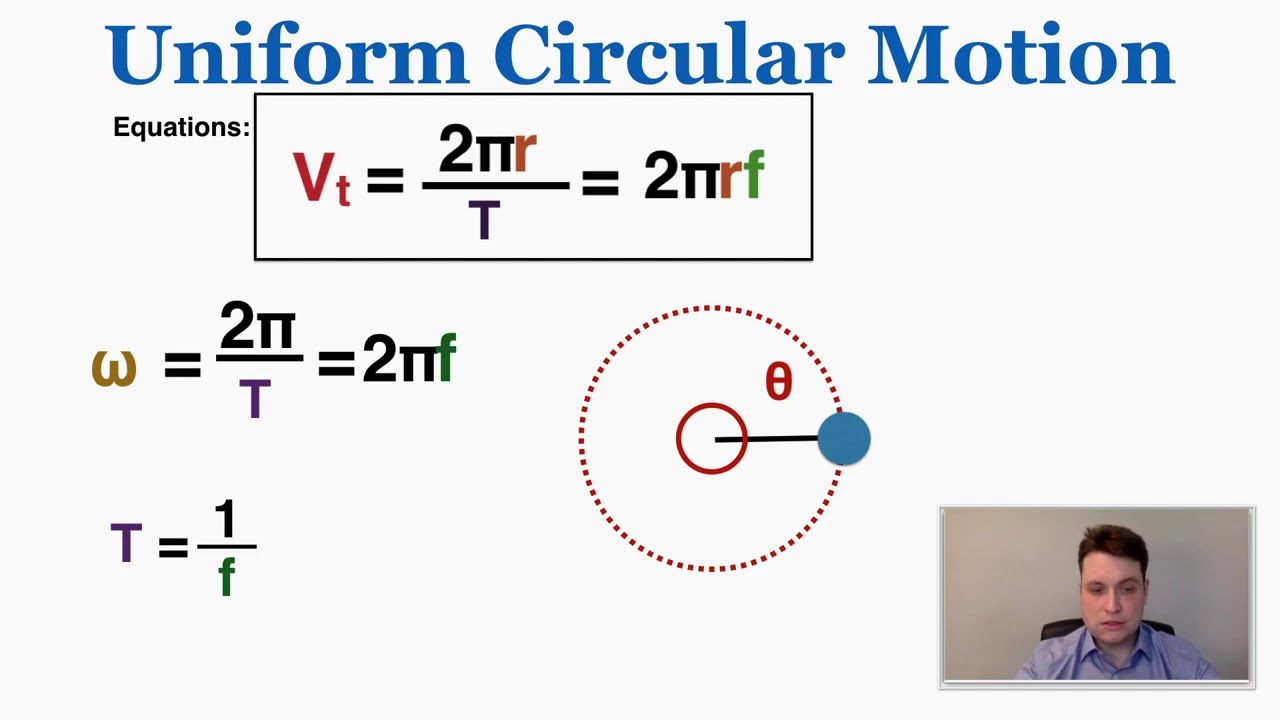
Why does a mass on a string in a circular motion tend to move upwards when the angle θ is less than a certain value?
-The tension in the string (T) can be resolved into components. When T sin θ equals the weight of the mass (mg), any increase in the horizontal component of tension (T cos θ), which provides the centripetal force, will cause the mass to move upwards if θ is less than the critical angle.
What is the concept of 'static friction' in the context of an object at rest on an inclined plane?
-Static friction is the force that opposes the initiation of motion between two surfaces in contact. It can vary from zero up to a maximum value, which is the product of the coefficient of static friction and the normal force.
Why is it incorrect to apply the formula for an object's acceleration down an inclined plane when the object is actually moving uphill?
-The formula for acceleration down an inclined plane is derived under the assumption of downhill motion. If the object is moving uphill, the direction of the frictional force would be opposite to what was assumed in the derivation, making the formula inapplicable.
How can the presence of friction affect the application of Newton's laws?
-Friction is a force that opposes motion and its direction is not fixed; it depends on the direction of motion. If the direction of motion is assumed in a problem, applying a formula derived under different assumptions can lead to incorrect conclusions.
What is the significance of the direction of the frictional force in the context of Newton's laws?
-The direction of the frictional force is crucial as it opposes the direction of motion. It is a dynamic force that adjusts based on the motion state of the object, and thus must be correctly identified in the application of Newton's laws.
How does the mass of an object affect its acceleration down an inclined plane?
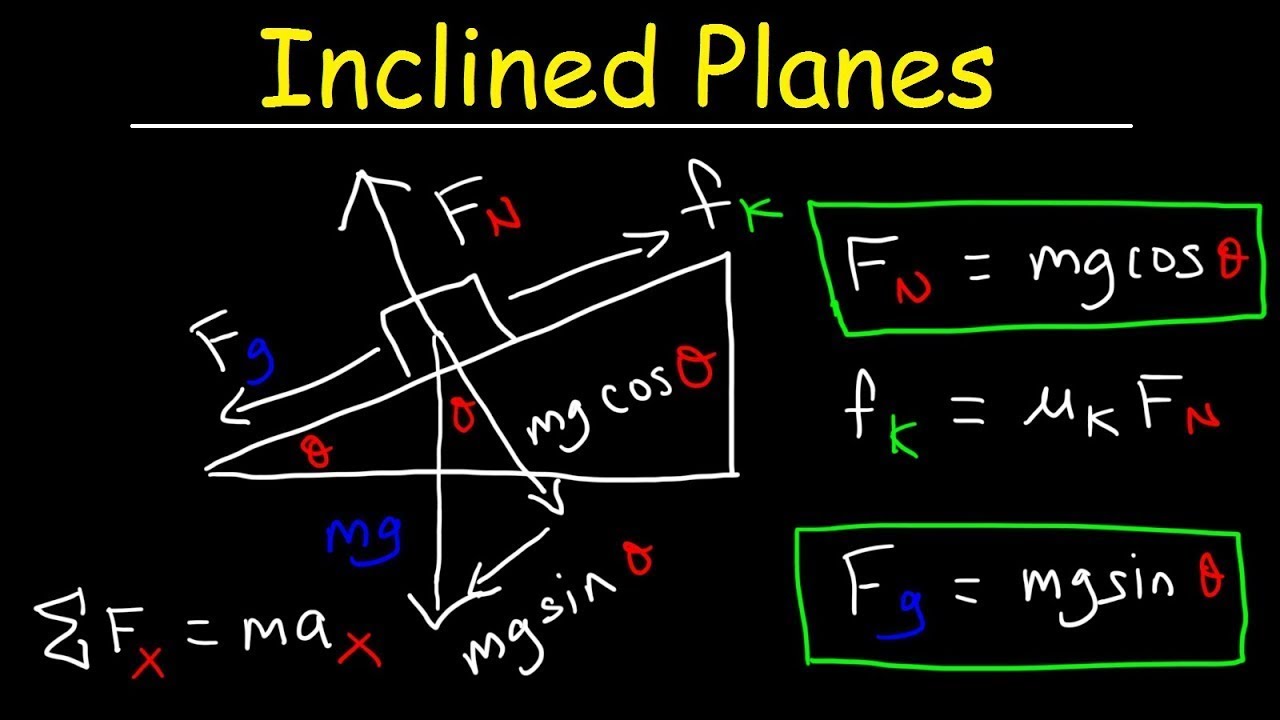
-The mass of the object cancels out in the equation for acceleration down an inclined plane (a = g sin θ), which means the acceleration is independent of the object's mass under the influence of gravity and the angle of the incline.
Outlines
😀 Interactive Learning Environment
The paragraph discusses the ideal class size for dialogue and addressing questions. It emphasizes the importance of student participation and the value of diverse perspectives in enriching the learning experience. The professor also mentions the pedagogical techniques they don't fully endorse and transitions into discussing the power of a fundamental law in physics.
📚 Application of Newton's Laws
This section focuses on the application of Newton's laws to predict future events based on current information. It uses a spring-mass system as an example to illustrate how to apply these laws. The professor explains the concept of force constants in relation to springs and how to determine the force exerted by a spring through experimentation.
🔍 Solving Differential Equations
The paragraph delves into solving differential equations, which are equations involving unknown functions and their derivatives. It discusses the process of guessing solutions and the importance of the Table of Integrals. The professor uses a simple harmonic motion example with a mass attached to a spring to demonstrate how to solve such equations and the importance of initial conditions in formulating the solution.
🧲 Incorporating Real-World Factors
The professor addresses the limitations of theoretical models by acknowledging the presence of friction in real-world scenarios. It discusses how unaccounted forces, such as friction, can lead to discrepancies between theoretical predictions and actual observations. The paragraph also touches on the relativistic dynamics as a more accurate description of motion at high speeds and quantum mechanics for very small objects.
🔄 Newton's Laws in Two Dimensions
This section introduces the application of Newton's laws in two dimensions. The professor explains the vector nature of forces and accelerations in such scenarios. Using a block on a table as an example, the discussion covers how to analyze forces and apply Newton's second law in vector form to determine the normal force and frictional force acting on the block.
📐 Forces and Motion on an Inclined Plane
The paragraph explores the concept of forces acting on an object placed on an inclined plane. It discusses the components of gravitational force and how they contribute to the object's potential motion. The professor also explains the role of static and kinetic friction in influencing the object's movement and how to calculate the critical angle at which the object will start sliding.
🤔 Analyzing Pulley Systems
This section examines the dynamics of a pulley system with two masses and a rope. The professor discusses how to calculate the tension in the rope and the acceleration of the masses. It emphasizes the importance of understanding the direction of acceleration and the role of friction in such systems. The paragraph also explores the conditions under which the system will move and the significance of the angle of inclination in determining the behavior of the system.
🎢 Physics of Amusement Park Rides
The professor discusses the physics behind amusement park rides, particularly those involving circular motion. It explains the role of centripetal force and the conditions required for an object to move in a circular path. The paragraph covers examples such as a mass attached to a string moving in a circle, the banking of racetracks to facilitate turns without friction, and the principles behind loop-the-loop rides, emphasizing the critical speed required to prevent falling.
Mindmap
Keywords
💡Dialogue
💡Pedagogical Techniques
💡Laws of Physics
💡Differential Equation
💡Newton's Laws
💡Friction
💡Relativistic Dynamics
💡Quantum Mechanics
💡Electrical Force
💡Inclined Plane
💡Coefficient of Static Friction
Highlights
The importance of small class sizes for fostering dialogue and understanding student perspectives.
Encouragement for students to actively participate by interrupting, asking questions, and discussing related issues.
The professor's enthusiasm for the dynamic nature of teaching due to the variety of students and their unique questions.
The use of a historical physics law to explain mechanical phenomena and its application through concrete examples.
The process of predicting future events in physics by understanding the present state and applying physical laws.
The concept that all problems in physics can be categorized based on the information given about the present state.
The illustration of a simple physics problem involving a table, a spring, and a mass to demonstrate the use of physical laws.
The explanation of how to derive the force exerted by a spring through experimental methods.
The transformation of physical laws into differential equations to deduce the behavior of a system over time.
The importance of guessing in solving differential equations and the role of the Table of Integrals.
The selection of trigonometric functions as a solution to a differential equation representing oscillatory motion.
The consideration of initial conditions in physics problems to match the specific scenario being studied.
The limitations of Newton's laws and the conditions under which they are valid, such as non-relativistic and macroscopic scales.
The role of friction in real-world physics problems and its impact on the accuracy of theoretical predictions.
The process of identifying and quantifying new forces, such as electrical forces, through experimental observations.
The concept of forces as vectors and the need to resolve them into components along different axes.
The application of Newton's laws to problems involving inclined planes and the introduction of friction into these scenarios.
The critical angle for an object to start sliding down an inclined plane based on the coefficient of static friction.
The use of simultaneous equations to solve for tensions in a system with multiple masses and a pulley system.
The conditions under which a formula derived from Newton's laws can be applied and the importance of considering the domain of the problem.
The role of centripetal acceleration in circular motion and how it allows objects to move in a circle without falling towards the center.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: