2011 Calculus AB free response #3 (a & b) | AP Calculus AB | Khan Academy
TLDRThe video script discusses the problem of finding the equation for a tangent line to the function f(x) = 8x^3 at the point where x equals 1/2, and then calculating the area of a region in the first quadrant enclosed by the graphs of f(x) and g(x) = sin(πx). The solution involves determining the derivative of f(x) to find the slope of the tangent line, using the point-slope form to derive the line's equation (y = 6x - 2). For the area calculation, the script explains the process of integrating with respect to x from 0 to 1/2 to find the area under the curve of g(x), and then subtracting the area under f(x), resulting in a final area expression involving pi and a rational number.
Takeaways
- 📌 The problem involves finding the equation of a tangent line and calculating the area of a region in the first quadrant.
- 🔍 The function f(x) = 8x^3 is given, and the tangent line at x = 1/2 needs to be found.
- 🧮 To find the tangent line, the derivative of the function f(x) is calculated, which is f'(x) = 24x^2.
- 📈 The slope of the tangent line at x = 1/2 is found by evaluating the derivative at this point, resulting in a slope of 6.
- 🤔 The equation of the tangent line is determined using the point-slope form and the known point (1/2, 1), yielding y = 6x - 2.
- 🌟 The area of the region R is bounded by the functions g(x) = sin(πx) above and f(x) = 8x^3 below.
- 📊 The area is calculated using integrals, specifically the integral of the top function g(x) minus the integral of the bottom function f(x) from 0 to 1/2.
- 🧮 The antiderivative of g(x) = sin(πx) is found to be -1/π cos(πx), and the antiderivative of f(x) = 8x^3 is -2x^4.
- 🧠 The area calculation involves evaluating these antiderivatives at the bounds 0 and 1/2 and then finding the difference.
- 🔢 The final area calculation results in an expression involving pi and simple arithmetic, yielding an area of -1/8 + 1/π.
- 🎓 The video script emphasizes the importance of understanding derivatives and antiderivatives for solving these types of problems.
Q & A
What is the main topic of the video?
-The main topic of the video is to find the equation for the tangent line to the graph of the function f(x) = 8x^3 at x = 1/2 and to calculate the area of the region enclosed by the graphs of functions f(x) and g(x) = sin(πx) in the first quadrant.
What is the value of f(1/2)?
-The value of f(1/2) is 1, since f(x) = 8x^3 and by substituting x = 1/2, we get 8 * (1/2)^3 = 1.
How is the slope of the tangent line determined?
-The slope of the tangent line is determined by finding the derivative of the function f(x) at x = 1/2. The derivative, f'(x) = 24x^2, gives the slope of the tangent line at any point x.
What is the slope of the tangent line at x = 1/2?
-The slope of the tangent line at x = 1/2 is 6, calculated by substituting x = 1/2 into the derivative f'(x) = 24x^2, resulting in 24 * (1/2)^2 = 6.
What is the equation of the tangent line at x = 1/2?
-The equation of the tangent line at x = 1/2 is y = 6x - 2, derived using the point-slope form with the slope m = 6 and the point (1/2, 1).
How is the area of region R calculated?
-The area of region R is calculated by integrating the difference between the functions g(x) = sin(πx) and f(x) = 8x^3 from 0 to 1/2.
What is the antiderivative of g(x) = sin(πx)?
-The antiderivative of g(x) = sin(πx) is -1/π * cos(πx), derived using the chain rule and properties of trigonometric functions.
What is the antiderivative of f(x) = 8x^3?
-The antiderivative of f(x) = 8x^3 is -2x^4/4, which simplifies to -x^4/2, found by increasing the exponent by 1 and dividing by the new exponent's corresponding coefficient.
What is the value of the definite integral of the area of region R from 0 to 1/2?
-The value of the definite integral is -1/8 + 1/π, obtained by evaluating the antiderivative of g(x) and f(x) from 0 to 1/2 and calculating their difference.
Why is the cosine term in the antiderivative of g(x) negative?
-The cosine term in the antiderivative of g(x) is negative to ensure that when the derivative is taken, the resulting function matches the original function g(x) = sin(πx).
Why does the final area calculation result in -1/8 + 1/π?
-The final area calculation results in -1/8 + 1/π because when evaluating the antiderivative of g(x) and subtracting the antiderivative of f(x) from 0 to 1/2, the cosine terms cancel out, leaving the negative of the constant terms from each antiderivative.
Outlines
📚 Calculus: Finding the Tangent Line and Area of a Region
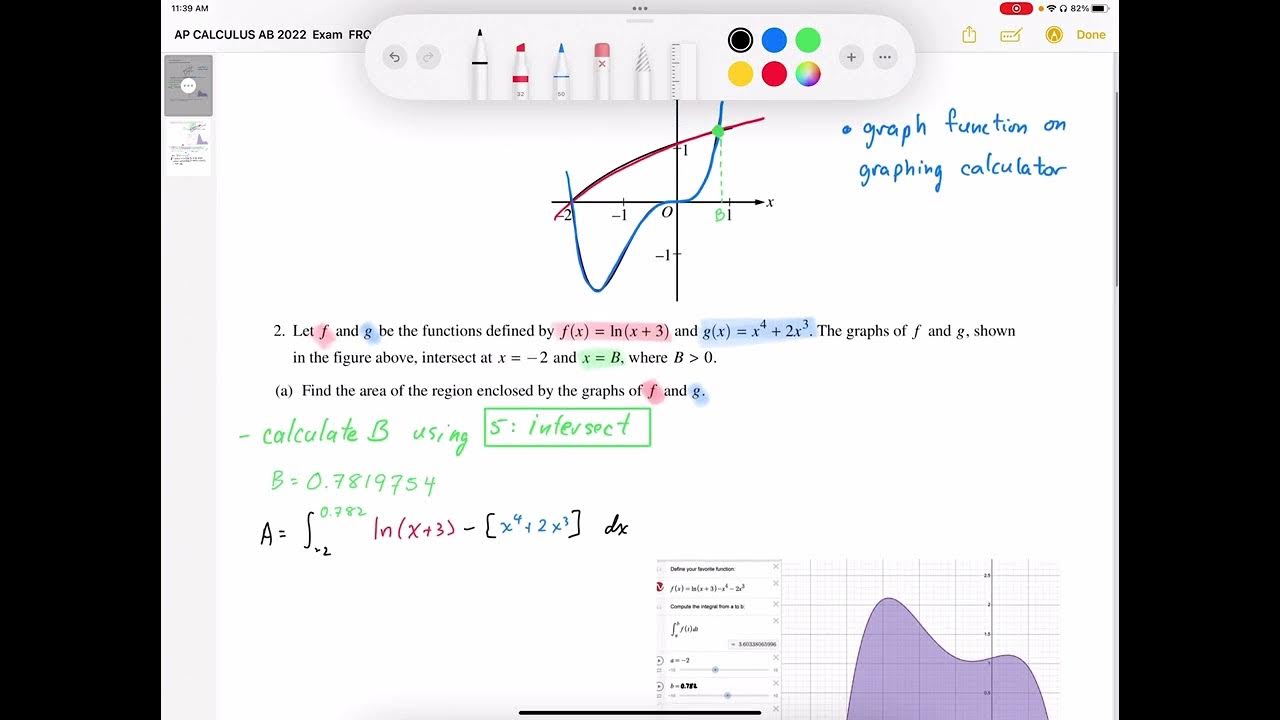
The paragraph begins with the setup of a mathematical problem in the first quadrant, defined by the functions f(x) = 8x^3 and g(x) = sin(πx). The task is to find the equation of the tangent line to the graph of f at x = 1/2. The process involves calculating the derivative of f(x), which is f'(x) = 24x^2, and evaluating it at x = 1/2 to get a slope of 6. Using the point (1/2, 1) and the slope, the equation of the tangent line is derived as y = 6x - 2. The second part of the problem involves finding the area of the region R, which is bounded by the functions f(x) and g(x). The area is calculated using integration, with the integral of sin(πx) from 0 to 1/2 being -1/π cos(π/2) + 2(1/2)^4, and the integral of 8x^3 from 0 to 1/2 being -2x^4/4 evaluated from 0 to 1/2. The final area is determined by combining these results.
📘 Antiderivatives and Area Calculation
This paragraph delves into the calculation of antiderivatives and the area under a curve. The antiderivative of sin(πx) is determined to be -1/π cos(πx), and the antiderivative of -8x^3 is -2x^4/4. The area under the curve of sin(πx) from 0 to 1/2 is evaluated, which results in 0 after simplification, since cos(π/2) is 0. The area calculation also involves subtracting the area under the curve of -8x^3 from 0 to 1/2, which is -1/8. The final area of the region R is given as -1/8 + 1/π, which is the result of the area between the two functions within the specified interval.
Mindmap
Keywords
💡tangent line
💡derivative
💡slope-intercept form
💡antiderivative
💡area of a region
💡integration
💡point-slope form
💡function
💡intersection point
💡chain rule
💡standard form
Highlights
The problem involves finding the equation for a tangent line to a function in the first quadrant.
The function f(x) is given as f(x) = 8x^3, and the tangent line is sought at x = 1/2.
The value of f(1/2) is calculated to be 1, providing a point on the graph (1/2, 1).
The slope of the tangent line is determined by finding the derivative of f(x) at x = 1/2, which is f'(x) = 24x^2.
The slope of the tangent line at x = 1/2 is found to be 6.
The equation of the tangent line is derived using the point-slope form, resulting in y = 6x - 2.
The area of the region R, enclosed by the graphs of the functions, is the focus of the second part of the problem.
The region R is bounded above by g(x) = sin(πx) and below by f(x) = 8x^3.
The area calculation involves an integral from 0 to 1/2, representing the area under the curve of g(x) minus the area under f(x).
The antiderivative of g(x) = sin(πx) is found to be -1/π cos(πx).
The antiderivative of f(x) = 8x^3 is determined to be -2x^4/4, or -x^4/2.
The area under g(x) from 0 to 1/2 is calculated, and the area under f(x) is subtracted to find the area of region R.
The final expression for the area of R is simplified to -1/8 + 1/π, showcasing the integration process.
The problem-solving approach combines the use of derivatives for tangent lines and integrals for area calculations.
The problem demonstrates the application of calculus concepts in finding tangent lines and areas of geometric regions.
The process of solving the problem is explained in a step-by-step manner, emphasizing clear and logical mathematical reasoning.
The problem serves as an example of the practical use of calculus in computing geometric properties of functions.
The transcript provides a comprehensive walkthrough of the problem, suitable for educational purposes and understanding of calculus techniques.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: