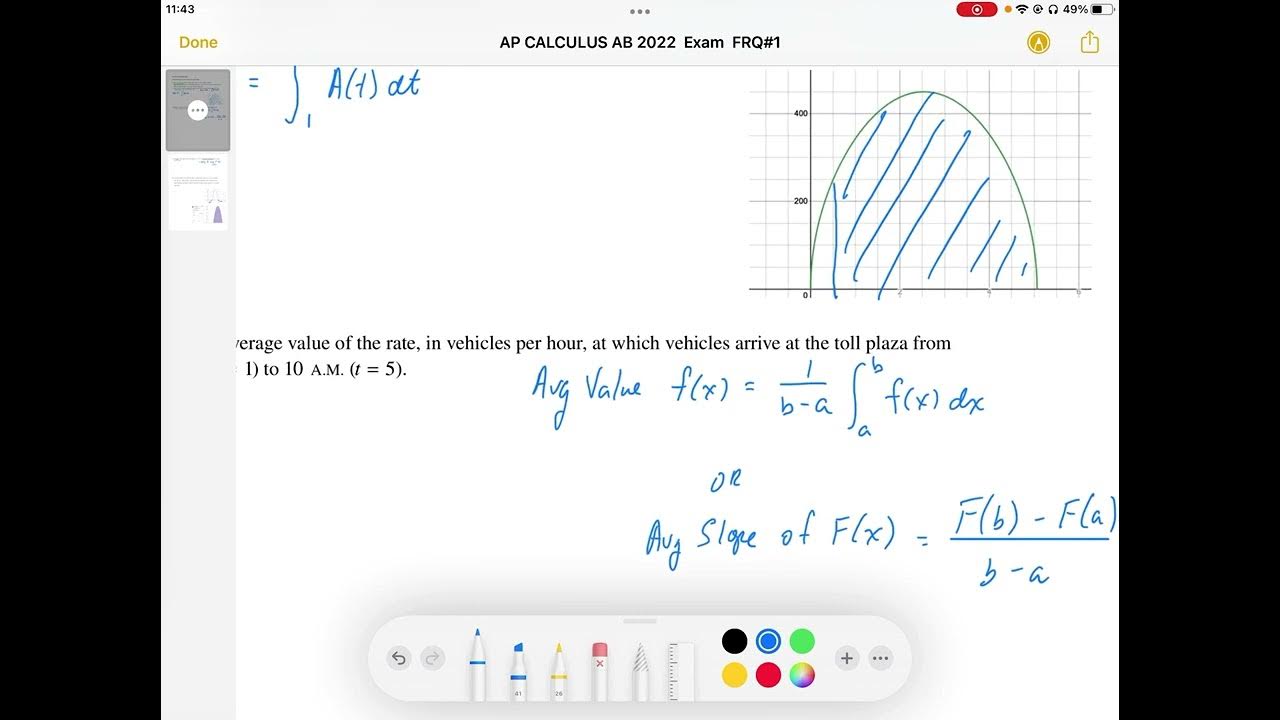
AP CALCULUS AB 2022 Exam Alternate (LONG) Solution FRQ#1c
TLDRThe video script discusses the rate at which vehicles arrive at a toll plaza at six in the morning. The presenter begins by differentiating the rate function, denoted as 'a', to find the rate of change, or 'a prime'. Using the chain rule, the derivative is calculated, resulting in an expression involving cosine and sine functions. The derivative at t equals one is then evaluated, leading to a value of 140.8, which is positive. This positive value indicates that the rate of change is increasing at that specific time, suggesting a growing number of cars per hour arriving at the toll plaza.
Takeaways
- 📈 The question is about determining if the rate at which vehicles arrive at a toll plaza at 6 AM is increasing or decreasing.
- 🔍 To answer this, we need to find the rate of change, which involves differentiating the rate function, denoted as 'a'.
- 🧮 The differentiation process involves applying the chain rule to the square root and cosine functions within the rate function.
- 📚 The derivative of the rate function, 'a prime of t', is calculated to determine the rate of change at a specific time 't'.
- 🕒 The specific time chosen for evaluation is t equals 1, which corresponds to 6 AM.
- 🔢 The derivative at t=1 is simplified to involve cosine and square root of sine functions with specific values.
- 📱 The final expression is plugged into a graphing calculator to find the numerical value of the derivative at t=1.
- 🔧 After calculation, the derivative at t=1 is found to be approximately 140.8, which is a positive value.
- ↗️ Since the derivative is positive, it indicates that the rate of change is increasing at t=1.
- 🚗 This implies that at 6 AM, more vehicles are arriving at the toll plaza per hour compared to the previous hour.
- ⏱️ The rate function and its derivative provide insight into the traffic flow trends at the toll plaza over time.
- 📈 Understanding the rate of change is crucial for predicting and managing traffic congestion at peak hours.
Q & A
What is the main question being addressed in the transcript?
-The main question is whether the rate at which vehicles arrive at the toll plaza at six am is increasing or decreasing, and the reason for this trend.
What is the mathematical approach to determine the rate of change?
-The approach involves differentiating the rate function 'a' with respect to time 't' to find the rate of change, denoted as 'a prime'.
What is the rate function 'a' in the context of the transcript?
-The rate function 'a' is not explicitly given in the transcript, but it is implied to be a function that describes the rate of vehicle arrivals at the toll plaza.
How is the derivative 'a prime of t' calculated?
-The derivative is calculated by applying the chain rule to the square root of sine to the power of negative one-half, resulting in a function involving cosine and sine functions.
What specific value of 't' is used to evaluate the rate of change?
-The value t equals 1 is used to evaluate the rate of change at six am.
What is the final expression for the derivative 'a prime of t'?
-The final expression is 225 times the cosine of 0.62t, divided by the square root of the sine of 0.62t.
What does the value of the derivative at t equals 1 indicate about the rate of change?
-The value of the derivative at t equals 1 is positive, indicating that the rate of change is increasing at that specific time.
What tool was suggested for further evaluation of the derivative?
-A graphing calculator is suggested for further evaluation of the derivative to find its numerical value.
What is the numerical value of the derivative at t equals 1?
-The numerical value of the derivative at t equals 1 is approximately 140.8, indicating an increasing rate of vehicle arrivals.
What does the positive value of the derivative imply for the vehicle arrival rate?
-A positive value of the derivative implies that the rate at which vehicles are arriving at the toll plaza is increasing at six am.
Why is it important to determine if the rate is increasing or decreasing?
-Determining if the rate is increasing or decreasing is important for understanding traffic patterns, planning staffing needs at the toll plaza, and potentially managing congestion.
What other factors might influence the rate of vehicle arrivals at the toll plaza?
-Factors such as traffic conditions, road closures, special events, and time of day can all influence the rate of vehicle arrivals at the toll plaza.
Outlines
📈 Calculating the Rate of Vehicle Arrival at Toll Plaza
The paragraph discusses the mathematical process of determining whether the rate at which vehicles arrive at a toll plaza at 6 AM is increasing or decreasing. The speaker begins by differentiating the rate function 'a' to find the rate of change, represented as 'a prime of t'. Using the chain rule, the derivative is calculated to be 225 * (0.62 cosine of T) divided by the square root of sine of 0.62. By substituting T equals 1 into the derivative, the rate of change is found to be positive, indicating an increasing rate of vehicle arrivals at that specific time.
Mindmap
Keywords
💡Rate
💡Toll Plaza
💡Differentiate
💡Derivative
💡Chain Rule
💡Square Root
💡Sine Function
💡Cosine Function
💡Graphing Calculator
💡Positive Rate of Change
💡Time (t=1)
Highlights
The rate at which vehicles arrive at the toll plaza at 6 am is being analyzed to determine if it's increasing or decreasing.
To find the rate of change, the rate function 'a' is differentiated to find 'a prime'.
Differentiating the square root term involves applying the chain rule and differentiating the sine function.
The derivative 'a prime of t' is simplified to involve cosine and square root of sine functions.
The derivative value at t equals 1 is calculated to determine the rate of change at that specific time.
The expression for the derivative at t=1 involves cosine of 0.62 and square root of sine of 0.62.
A graphing calculator is used to find the numerical value of the derivative at t=1.
The numerical value of the derivative 'a prime' at t=1 is approximately 140.8, indicating the rate in cars per hour.
Since the calculated rate of change is positive, it concludes that the rate of vehicle arrival is increasing at 6 am.
The problem-solving approach involves differentiating a given function and evaluating the derivative at a specific point.
The chain rule is essential for differentiating composite functions, such as those involving square roots and trigonometric functions.
The use of a graphing calculator aids in obtaining precise values for complex derivatives.
The sign of the derivative value indicates the direction of the rate of change, with positive values suggesting an increase.
The problem examines the application of calculus in real-world scenarios, such as analyzing traffic rates.
The process demonstrates the importance of simplifying expressions before plugging in values to find derivatives.
The problem-solving method can be applied to other rate-related questions in various contexts.
The transcript provides a step-by-step guide on how to approach and solve calculus problems involving rates of change.
Understanding the concept of derivatives is crucial for analyzing rates of change in different scenarios.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: