2021 AP Calculus AB Free Response #5

Allen Tsao The STEM Coach

6 May 202108:12

EducationalLearning

32 Likes 10 Comments

TLDRThe video transcript presents a detailed mathematical exploration of a function f(x), focusing on implicit differentiation to find the derivative dy/dx. The host then applies this derivative to determine the equation of a tangent line at a specific point on the curve, using slope-point form. The analysis continues with the identification of a horizontal tangent line by setting dy/dx to zero and solving for x and y. A second derivative test is employed to ascertain whether the function has a relative minimum or maximum at a particular point. The process involves complex algebraic manipulations and substitutions, ultimately leading to the conclusion that one point represents a relative minimum and another a relative maximum. The presenter acknowledges a mistake in the process and corrects it, emphasizing the importance of accuracy in mathematical computations.

Takeaways

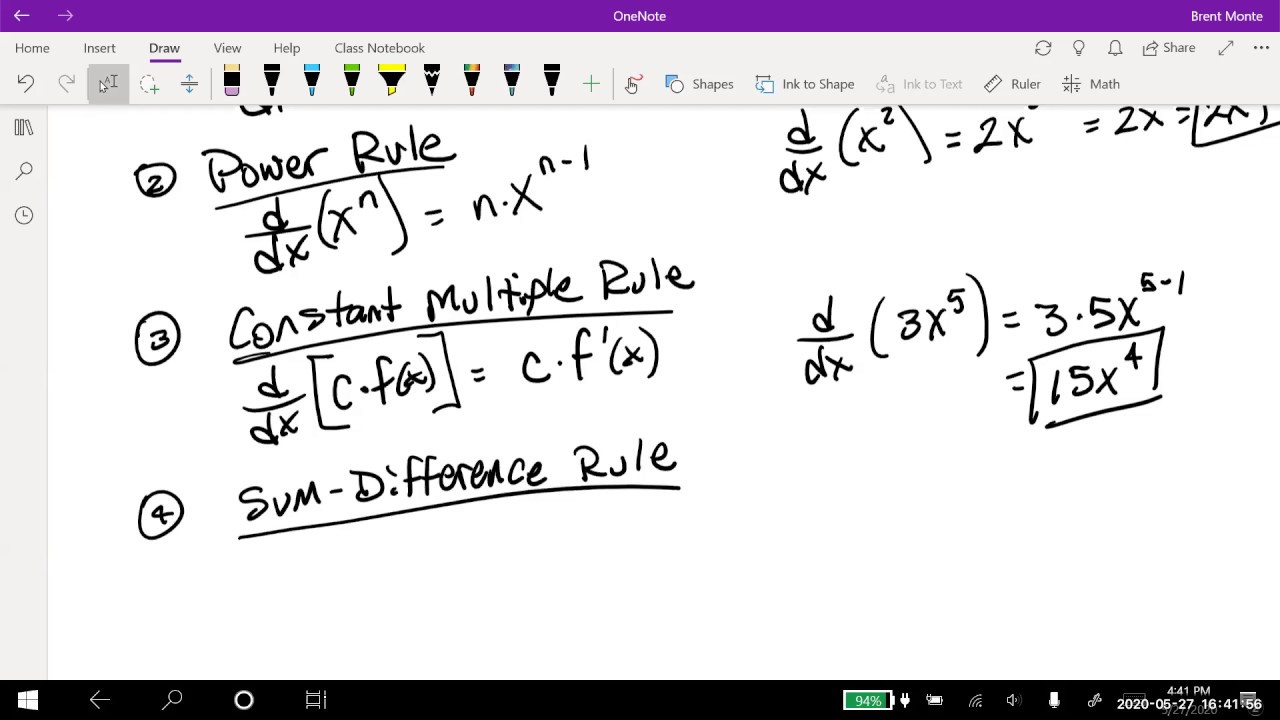
📚 Implicit differentiation is used to find the derivative of an equation where y is given implicitly as a function of x.
🔍 The derivative dy/dx is found by applying the product rule and chain rule to the given equation, resulting in dy/dx = ycos(x) / (4y - sin(x)).
📐 To find the equation of a tangent line at a specific point, use the slope-point form which requires the slope (dy/dx) and a point on the curve.
🔢 At the point (0, -√3), the slope of the tangent (dy/dx) is calculated using the values of y and x, which simplifies to 1/4.
🎢 The coordinates of the point where the tangent line is horizontal are found by setting dy/dx to zero and solving for x, which yields x = π/2.
🔑 The second derivative test is used to determine if a point is a relative minimum or maximum by analyzing the concavity of the function at that point.
🧮 The second derivative is calculated using the quotient rule, and the sign of this derivative indicates whether the function is concave up or down at the point of interest.
🔄 When dy/dx equals zero, it indicates a potential relative extremum, but further analysis with the second derivative is required to confirm.
🚫 The first derivative test cannot be used in this case due to the complexity of the derivative form, making the second derivative test more appropriate.
📍 The relative extremum is found at the point where both the first and second derivatives are zero, and the second derivative indicates the nature of the extremum.
✅ The final analysis concludes that the point (π/2, -3/2) is a relative minimum and the point (π/2, 2) is a relative maximum based on the second derivative test.

Q & A

What is the main topic discussed in the transcript?
-The main topic discussed in the transcript is the process of implicit differentiation and finding the equation of a tangent line to a curve at a given point.
What is the function f(x) represented by in the transcript?
-The function f(x) is represented by an equation involving y, where the derivative dy/dx is shown to be equal to y/(4y^2 - 6).
What method is used to find the slope of the tangent line at a specific point on the curve?
-Implicit differentiation is used to find the slope of the tangent line at a specific point on the curve.
How is the equation of the tangent line at a point found?
-The equation of the tangent line at a point is found by using the slope-point form, which requires the slope (dy/dx) at that point and the coordinates of the point.
What does it mean for a tangent line to be horizontal?
-A horizontal tangent line means that the derivative dy/dx is equal to zero at that point.
How is a relative minimum or maximum determined for the function?
-A relative minimum or maximum is determined by using the second derivative test, which involves finding the sign of the second derivative at the point in question.
What is the significance of the second derivative being positive or negative?
-If the second derivative is positive, it indicates that the function is concave up at that point, which means it is a relative minimum. If it is negative, it indicates the function is concave down, which means it is a relative maximum.
What is the point at which the tangent line is horizontal?
-The point at which the tangent line is horizontal is found when the first derivative dy/dx equals zero. In the transcript, this occurs when y = 0 or cos(x) = 0, with the specific x values being π/2 and 3π/2 within the given interval.
What is the mistake made in the transcript regarding the coordinates of the point?
-The mistake made in the transcript is not actually calculating the y-coordinate for the given x-values when dy/dx equals zero, which is necessary to determine the exact coordinates of the point.
How is the y-coordinate found for the point where the tangent line is horizontal?
-The y-coordinate is found by plugging the x-value into the original equation of the curve and solving for y. In the transcript, this involves solving 2y^2 - y - 6 = 0, which gives y = -3/2 and y = 2.
What is the final conclusion about the relative extrema of the function at the points found?
-The final conclusion is that the point (π/2, -3/2) is a relative minimum and the point (π/2, 2) is a relative maximum, based on the sign of the second derivative at these points.
What would happen if the second derivative test failed?
-If the second derivative test failed, meaning if the second derivative was also zero, it would not be possible to claim the point as a relative minimum or maximum, and a different technique would need to be attempted.

Outlines

00:00

📚 Implicit Differentiation and Tangent Line Equation

This paragraph discusses the process of implicit differentiation to find the derivative of a function represented by an equation. The focus is on deriving the equation of the tangent line to a curve at a specific point, using the slope-point form. The speaker calculates the derivative at a given point, (0, √3), and simplifies the expression to find the slope of the tangent line. The process involves applying the product rule and factoring out terms to isolate dy/dx. The resulting equation of the tangent line is then formulated.

05:01

🔍 Finding Horizontal Tangent and Analyzing Function Extremes

The second paragraph delves into finding the points where the tangent line to the curve is horizontal, which corresponds to when the derivative dy/dx equals zero. The speaker sets up an equation to find these points and simplifies it using the properties of trigonometric functions. After identifying potential points, the speaker narrows down the solutions to those within a specific domain. The paragraph concludes with a discussion on using the second derivative test to determine whether the function has a relative minimum or maximum at the identified points. The speaker calculates the second derivative and evaluates its sign to classify the nature of the critical points.

Mindmap

Keywords

💡Implicit Differentiation

Implicit differentiation is a method used to find the derivative of an equation that is not explicitly solved for y. It involves differentiating both sides of the equation with respect to x, treating y as a function of x. In the video, it is used to find the derivative dy/dx of the given function f(x), which is crucial for determining the slope of the tangent line at a specific point on the curve.

💡Product Rule

The product rule is a fundamental theorem in calculus that is used to find the derivative of a product of two functions. It states that the derivative of the product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function. In the script, the product rule is applied when differentiating y * cos(x), which is part of the process to find dy/dx.

💡Slope-Point Form

The slope-point form of a line is a way to express the equation of a line when the slope and a point on the line are known. It is given by the formula y - y1 = m(x - x1), where m is the slope and (x1, y1) is the point on the line. In the video, the slope-point form is used to write the equation of the tangent line to the curve at a given point, which requires finding the slope (dy/dx) at that point.

💡Horizontal Tangent Line

A horizontal tangent line to a curve at a certain point means that the slope of the tangent line at that point is zero. This occurs when the derivative of the function, dy/dx, is equal to zero. In the context of the video, finding where dy/dx equals zero helps to determine points where the tangent to the curve is horizontal.

💡Second Derivative Test

The second derivative test is a method used to determine whether a point on a curve is a relative minimum, relative maximum, or neither. It involves finding the second derivative of the function and analyzing its sign around the point in question. In the video, the second derivative test is used to analyze the nature of the points found where the tangent line is horizontal.

💡Quotient Rule

The quotient rule is a theorem in calculus that allows us to differentiate functions that are quotients of two other functions. It states that the derivative of the quotient of two functions is the denominator times the derivative of the numerator minus the numerator times the derivative of the denominator, all divided by the square of the denominator. In the script, the quotient rule is used to find the second derivative of the given function.

💡Concave Up/Down

A function is said to be concave up if the second derivative is positive and concave down if the second derivative is negative. This concept is used to analyze the shape of the function's graph. In the video, the term 'concave up' is used to describe the shape of the function at a point where the second derivative is positive, indicating a relative minimum.

💡Relative Minimum/Maximum

A relative minimum (or maximum) of a function is a point where the function's value is less (or greater) than the function's values at all points in a neighboring region, but not necessarily less (or greater) than the function's values throughout its entire domain. In the video, the terms are used to classify the critical points found using the second derivative test.

💡Critical Points

Critical points are points on the graph of a function where the derivative is either zero or undefined. They often play a role in identifying local maxima, local minima, or points of inflection. In the context of the video, critical points are found by setting the first derivative dy/dx to zero and are then analyzed to determine the nature of the function at those points.

💡Derivative

The derivative of a function at a certain point gives the slope of the tangent line to the graph of the function at that point. It is a fundamental concept in calculus that describes the rate of change of a function. In the video, finding the derivative is essential for determining the slope of the tangent line and for analyzing the behavior of the function.

💡Tangent Line

A tangent line to a curve at a given point is a straight line that 'touches' the curve at that point without crossing it. The slope of the tangent line is equal to the derivative of the function at that point. In the video, finding the equation of the tangent line is a key step in understanding the curve's behavior at specific points.

Highlights

The process involves using implicit differentiation to find the derivative of the given function.

The derivative is found to be dy/dx = y*cos(x) / (4y - sin(x)).

The slope of the tangent line at a given point is calculated using the derivative at that point.

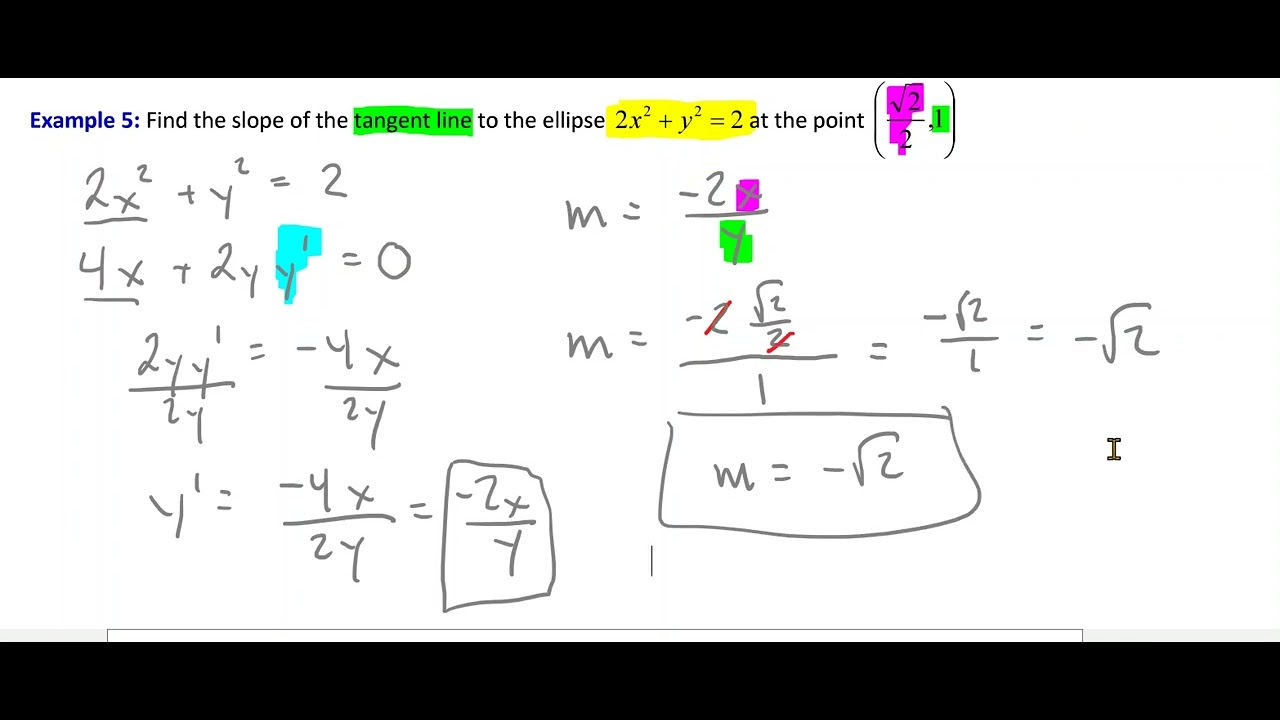
The coordinates of the point for the tangent line are determined to be (0, √3) and the slope is 1/4.

The condition for a horizontal tangent line is dy/dx = 0, which simplifies to y*cos(x) = 0.

The points where the tangent is horizontal are found to be at x = π/2 and x = 3π/2.

The second derivative test is used to determine if the function has a relative minimum or maximum at the given points.

The second derivative is calculated using the quotient rule and product rule.

The second derivative at the point (π/2, -3/2) indicates a relative minimum because it is concave up.

The second derivative at the point (π/2, 2) indicates a relative maximum because it is concave down.

The original equation 2y^2 - 6 = y*sin(x) is used to find the y-coordinates of the points.

The y-coordinates for the points are found to be -3/2 and 2 by solving the equation for y.

The process includes a correction for an oversight in finding the exact coordinates of the points.

The final coordinates for the points of interest are (π/2, -3/2) and (π/2, 2).

The presenter emphasizes the importance of checking computations, especially when done quickly.

The transcript provides a detailed walkthrough of calculus problems, including implicit differentiation and second derivative tests.

The mathematical process is explained step-by-step, allowing for a clear understanding of how to approach similar problems.

The transcript demonstrates the application of calculus in finding slopes of tangent lines and analyzing the concavity of curves.

The presenter uses a combination of algebraic manipulation and calculus to solve for the properties of the curve.

Transcripts

Browse More Related Video

Implicit Differentiation

Math 11 - Section 1.5

Implicit Differentiation | Differentiation when you only have an equation, not an explicit function

Implicit Differentiation - Finding Equation of Tangent Line

Implicit Differentiation

2004 AP Calculus AB Free Response #4

2021 AP Calculus AB Free Response #5

Takeaways

Q & A

What is the main topic discussed in the transcript?

What is the function f(x) represented by in the transcript?

What method is used to find the slope of the tangent line at a specific point on the curve?

How is the equation of the tangent line at a point found?

What does it mean for a tangent line to be horizontal?

How is a relative minimum or maximum determined for the function?

What is the significance of the second derivative being positive or negative?

What is the point at which the tangent line is horizontal?

What is the mistake made in the transcript regarding the coordinates of the point?

How is the y-coordinate found for the point where the tangent line is horizontal?

What is the final conclusion about the relative extrema of the function at the points found?

What would happen if the second derivative test failed?