3 | FRQ (No Calculator) | Practice Sessions | AP Calculus AB

Advanced Placement
17 Apr 202318:50
EducationalLearning
32 Likes 10 Comments

TLDRThe video script features a detailed mathematical discussion between Mark Kiraly and Virge Cornelius, focusing on a complex problem involving definite integrals, derivatives, and extreme value analysis. They delve into session three of an unspecified course, tackling a problem with four parts. The conversation covers evaluating the function F at specific points, determining intervals where the function is concave up and increasing, differentiating a composite function to find a derivative, and identifying the absolute maximum value of F on a closed interval. Throughout the session, they emphasize the importance of understanding mathematical concepts, using both analytical methods and graphical interpretation. The speakers also provide insights into exam strategies, such as time management, the use of fundamental theorems, and the significance of clear communication in mathematical problem-solving.

Takeaways
  • 📚 **Session Overview**: The session focuses on solving a problem with four parts, involving the evaluation of a function defined by a definite integral and understanding its properties.
  • 🔢 **Function Evaluation**: To find F of negative 4 and F of 6, the function is evaluated by substituting the given values into the integral, considering the limits and the properties of definite integrals.
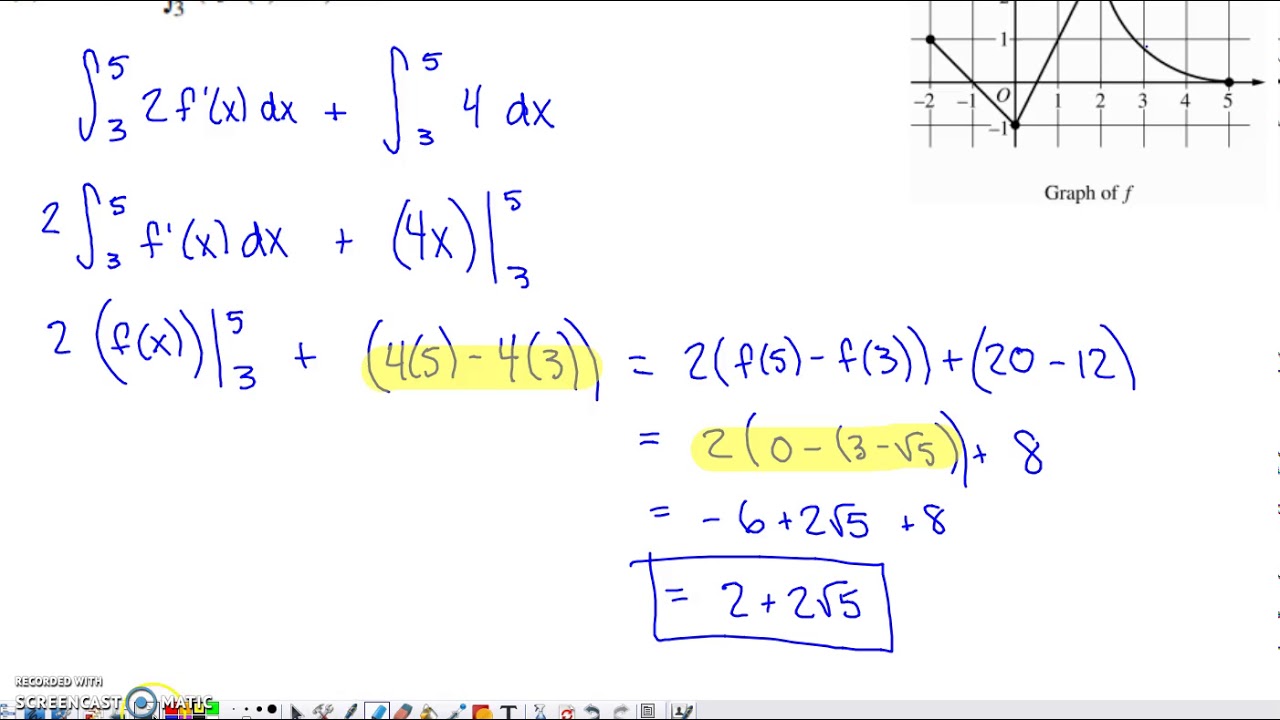
  • 📉 **Graph Understanding**: The integral's area under the curve is considered, and the graph of the function h(t) is used to understand the behavior of the integral over different intervals.
  • 🧮 **Algebraic Manipulation**: Anti-differentiation is used to solve the integral, applying the reverse power rule and considering the bounds of integration.
  • 📐 **Geometry and Calculus**: The areas under the curve are calculated using both geometrical methods and calculus, highlighting the importance of understanding both approaches.
  • ✏️ **No-Calculator Approach**: The problem is solved without a calculator, emphasizing the importance of strong algebraic and arithmetic skills.
  • 📈 **Increasing and Concave Up**: The function F is analyzed for intervals where it is concave up and increasing, which is determined by looking at the first and second derivatives.
  • 🔗 **Fundamental Theorem**: The fundamental theorem of calculus is used to find the derivative of F, which is essential in determining intervals of increase and concavity.
  • 🔄 **Chain Rule Application**: When finding C'(5.5), where C(x) = F(h(x)), the chain rule is applied by multiplying the derivative of the outer function with the derivative of the inner function.
  • 🏁 **Closed Interval Analysis**: To find the absolute maximum value of F on a closed interval, endpoints and critical points are considered as potential candidates for the maximum value.
  • ✍️ **Clear Communication**: Throughout the session, the importance of clear communication and showing work is emphasized for effectively conveying the problem-solving process.
Q & A

  • What is the topic of the session?

    -The session is about solving a problem involving definite integrals and their properties, specifically evaluating a function F at certain points and analyzing its behavior.

  • What is the function F defined as in the problem?

    -The function F is defined as a definite integral from 0 to x of h(t) dt, where h(t) is a given function represented by a graph.

  • What is the first part of the problem asking for?

    -The first part (Part A) asks for the values of F at 4 and F at 6.

  • How does one evaluate F of negative 4?

    -To evaluate F of negative 4, you substitute negative 4 for x, which becomes the upper limit of integration, and then apply the properties of definite integrals to find the area under the curve from 0 to negative 4.

  • What is the final answer for F of negative 4?

    -The final answer for F of negative 4 is negative 16/3.

  • What is the strategy for finding F of 6?

    -The strategy for finding F of 6 involves substituting 6 for x and calculating the definite integral from 0 to 6, considering the areas above and below the x-axis.

  • What is the significance of the function h being increasing?

    -The function h being increasing is significant because it relates to the first derivative of F (F prime) being positive, which is a condition for F to be increasing.

  • What is the open interval where F is concave up and increasing?

    -The open interval where F is concave up and increasing is from negative 4 to 0 and from 5.5 to 6.

  • What is the derivative of C with respect to x, given C(x) = F(h(x))?

    -The derivative of C with respect to x, denoted as C prime, is found using the chain rule and is equal to F prime of h(x) times h prime of x, evaluated at 5.5.

  • What is the value of C prime at x = 5.5?

    -The value of C prime at x = 5.5 is 4, which is calculated by multiplying F prime of h(5.5) with h prime of 5.5.

  • How is the absolute maximum value of F on the closed interval from negative 4 to 6 determined?

    -The absolute maximum value of F is determined by considering the endpoints of the interval and any critical points within the interval, then evaluating the function F at these points to find the highest value.

  • What is the absolute maximum value of F on the closed interval from negative 4 to 6?

    -The absolute maximum value of F on the closed interval from negative 4 to 6 is 2, which occurs at x equals 2.

Outlines
00:00
📚 Session Introduction and Problem Overview

The video script begins with an introduction by Mark Kiraly and Virge Cornelius, who are educators at Lafayette High School in Oxford, Mississippi. They are about to start session three, which involves a free-response question. The session includes a graphical step, and the handout for the session is mentioned. The problem they are tackling is divided into four parts, with the first part focusing on finding the values of F of 4 and F of 6 using a definite integral function. The discussion involves substituting values into the integral and considering the properties of definite integrals, including the use of anti-differentiation and the reverse power rule.

05:01
📉 Analyzing the Function's Graph and Calculating Areas

The second paragraph delves into the calculation of definite integrals by considering the areas under the curve of the function h(x). The discussion involves identifying positive and negative areas and using geometric properties to simplify the calculations. The speakers use symmetry to cancel out opposite areas and apply the concept of base times height to find the area of triangles. They also touch upon the use of the fundamental theorem of calculus to find the derivative of the integral function F(x), which leads to an analysis of when F(x) is concave up and increasing. The speakers provide a detailed explanation of how to determine the intervals where F(x) is increasing based on the first and second derivatives.

10:02
🔄 Derivatives and the Chain Rule Application

In the third paragraph, the focus shifts to finding the derivative of a composite function C(x), which is defined as C(x) = F(h(x)). The task is to find C'(5.5), which involves applying the chain rule. The speakers discuss the need to understand the derivative of the outside function and multiply it by the derivative of the inside function. They also emphasize the importance of understanding the graph of h(x) to evaluate the derivative accurately. The calculation involves finding the slope of the line segment at x = 5.5 and the value of h(5.5), leading to the final result of C'(5.5) being 4.

15:05
🔍 Extreme Value Theorem and Candidates for Maximum Value

The final paragraph addresses the problem of finding the absolute maximum value of F on the closed interval from negative 4 to 6. The speakers discuss the extreme value theorem and suggest using a candidates test to find the maximum value. They identify the endpoints of the interval and critical numbers where F'(x) equals zero. The process involves creating a table with the x-values and corresponding y-values of F(x) to determine the maximum value. The speakers also emphasize the importance of clear communication in the solution process, ensuring that the examiner can follow the reasoning without needing to infer the thought process. The absolute maximum value is found to be 2, occurring at x = 2, and the speakers provide a justification for this conclusion.

Mindmap
Keywords
💡Definite Integral
A definite integral is a fundamental concept in calculus that represents the accumulated value of a function over an interval. It is used to calculate the area under a curve. In the video, the function F is defined as a definite integral, and the speakers use it to find the values of F at specific points, such as F(-4) and F(6), by substituting the respective values into the upper limit of integration.
💡Free-Response Question
A free-response question is a type of assessment that requires students to write out their answers in their own words, rather than choosing from multiple-choice options. These questions often appear in exams like the AP (Advanced Placement) and are designed to test a student's understanding and ability to apply concepts. In the video, the speakers are discussing a free-response question related to calculus.
💡Anti-differentiation
Anti-differentiation, also known as integration, is the process of finding a function that, when differentiated, yields another given function. It is the reverse of finding the derivative. In the video, the concept is used when the speaker needs to find the integral of the function h(t) to evaluate F(-4) and F(6), which involves anti-differentiating the function.
💡Concave Up/Down
Concave up or concave down refers to the curvature of a function's graph. A function is concave up when its graph curves like a U shape, and concave down when it curves in the opposite direction. These terms are used in the video to describe the behavior of the function F and to determine intervals where F is increasing based on its second derivative.
💡Chain Rule
The chain rule is a fundamental theorem in calculus for deriving the derivative of a composite function. It states that the derivative of a composition of functions is the product of the derivative of the outer function and the derivative of the inner function. In the video, the chain rule is mentioned in the context of finding the derivative of the function C(x) = F(h(x)) at a specific point.
💡Product Rule
The product rule is a formula used to find the derivative of a product of two functions. It states that the derivative of the product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function. Although not explicitly used in the calculations shown in the video, it is a related concept that could be relevant in differentiating more complex expressions.
💡Extreme Value Theorem
The extreme value theorem is a fundamental theorem in calculus that states that if a function is continuous on a closed interval, then it attains both a maximum and a minimum value on that interval. In the video, the speakers use this theorem to find the absolute maximum value of the function F on the closed interval from -4 to 6.
💡Critical Numbers
Critical numbers are the points at which the derivative of a function is either zero or undefined. They are important in calculus because they often correspond to local maxima, local minima, or points of inflection. In the video, the speakers identify critical numbers by finding where the derivative of F (which is the same as h) equals zero to determine potential maximum or minimum values of F.
💡X-Intercepts
X-intercepts, also known as zeros or roots, are the points where a function or graph intersects the x-axis, which means the function's value is zero at these points. In the video, the speakers use the x-intercepts of the function h to help identify critical numbers and to evaluate definite integrals geometrically.
💡Fundamental Theorem of Calculus
The fundamental theorem of calculus is a theorem that links the concept of differentiating and integrating, showing that these two operations are essentially the inverse of each other. Specifically, it states that if a function is integrated and then differentiated, the original function is retrieved. In the video, the speakers refer to this theorem when discussing the derivative of the integral of h(t) with respect to x.
💡Graph Interpretation
Graph interpretation involves understanding and analyzing the graphical representation of mathematical functions or data. It is a crucial skill in calculus for visualizing and solving problems. In the video, the speakers frequently refer to the graph of h to interpret the behavior of the function F, such as its increasing/decreasing intervals and concavity.
Highlights

Session three begins with a free-response question focused on evaluating a function defined as a definite integral.

The problem is divided into four parts, starting with finding the values of F of 4 and F of 6.

Mark Kiraly and Virge Cornelius discuss the importance of downloading the handout for the session.

The definite integral is evaluated by substituting -4 and 6 for x, considering the function h(t).

A property of definite integrals is used to rewrite the integral from a negative to a positive limit.

The function h(x) is identified as the square root of 4 plus the square root of x.

The reverse power rule is applied for anti-differentiation, and the integral is solved without a calculator.

The value of F(-4) is calculated to be -16/3, showcasing the complexity of the no-calculator question.

For F(6), the area under the curve is evaluated geometrically, highlighting the use of symmetry in the graph.

The function F is analyzed for concavity and monotonicity, leading to the determination of intervals where F is concave up and increasing.

The fundamental theorem of calculus is used to find the derivative of F, which is equal to h(x).

The derivative of h(x) is considered to determine where F is increasing, using the graph for visual aid.

The function C(x) is introduced, defined as F(h(x)), and its derivative C'(5.5) is calculated using the chain rule.

The graph of h(x) is used to evaluate the derivative at a specific point, emphasizing the importance of visual analysis.

The absolute maximum value of F on the closed interval from -4 to 6 is found using the extreme value theorem and a candidates test.

Candidates for extreme values include endpoints and critical numbers where F'(x) equals zero or is undefined.

The maximum value of F is determined to be at x = 2, with a value of 2, using a combination of analytical and geometric methods.

The importance of clear communication and showing work is emphasized for readers of the exam papers.

The session concludes with advice on using both the fundamental theorem and geometry when evaluating definite integrals.

Transcripts

Browse More Related Video

5 | MCQ | Practice Sessions | AP Calculus AB

2 | FRQ (Calculator Active) | Practice Sessions | AP Calculus AB

6 | FRQ (Calculator Active) | Practice Sessions | AP Calculus AB

2022 Live Review 5 | AP Calculus AB | Focusing on the Big Theorems Including IVT, EVT, & MVT

2019 AP Calculus AB & BC Free Response Question #3

AP Calculus Practice Exam Part 8 (FR #4)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
AP CalculusIntegralsDerivativesConcavityMark KiralyVirge CorneliusMath StrategiesExam PrepEducational ContentNo-CalculatorProblem SolvingMathematical Analysis