AP Calculus Practice Exam Part 8 (FR #4)
TLDRThis video script is a detailed walkthrough of a calculus problem involving the function 'f' and its properties. The instructor guides students through evaluating the function 'g(x)' as an integral of 'f(t)', calculating areas under the curve, and finding critical points for absolute minimum values. The session delves into concepts like concavity, derivatives, and the fundamental theorem of calculus, with an emphasis on problem-solving strategies and understanding graphical representations of functions.
Takeaways
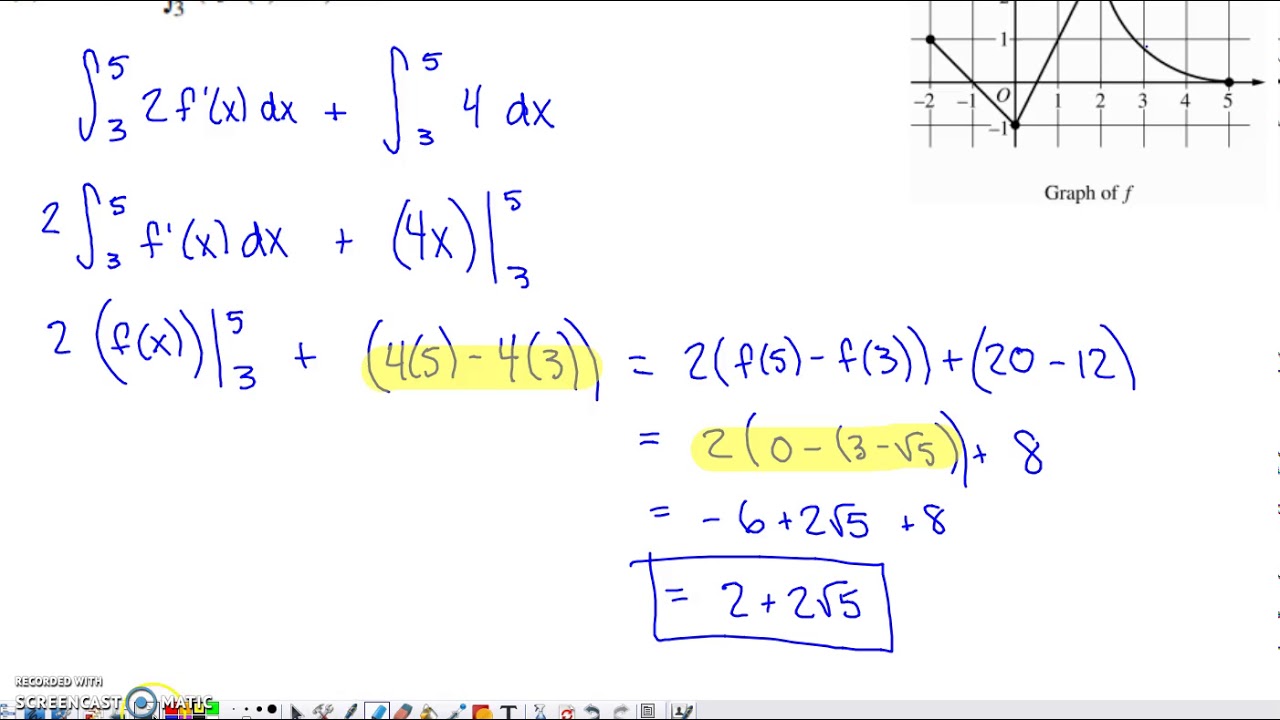
- 📈 The script discusses a problem involving the graph of a function f from -4 to 4, with horizontal tangents at specific points and a parabola in the last segment.
- 📚 The areas under the curve for regions A and B are given as 3 and 5, respectively, which are used to calculate the integral of f from -4 to 0.
- 🧩 The function g(x) is defined as the integral from -4 to x of f(t) with respect to t, which is used to find g(0) and g(4).
- 🔍 The integral calculus concept is explained as finding the area under the curve, which is applied to calculate g(0) by breaking it into two parts: a triangle and a negative area.
- ✂️ The calculation of g(4) involves breaking the integral into pieces, using previously calculated areas and integrating the given function over the interval [1, 4].
- 📝 The process of finding the antiderivative is demonstrated, which is essential for evaluating definite integrals and is used to find g(4).
- 📉 The concept of concavity is introduced, explaining how to determine if a function is concave up or down by analyzing the second derivative.
- 🔑 The fundamental theorem of calculus is referenced, stating that the derivative of an antiderivative is the original function, which helps in finding g'(x).
- 📌 The script identifies critical points of f by finding where the derivative is zero, which are used to find the absolute minimum value of g on the interval [-4, 4].
- 📐 The method for finding absolute minimums or maximums on a closed interval is outlined, emphasizing the importance of evaluating the function at the endpoints as well as at critical points.
- 📝 The final part of the script involves identifying intervals where the function g(x) is concave down, using the graph of f and the concept of points of inflection.
Q & A
What is the main topic discussed in the transcript?
-The main topic discussed in the transcript is the process of solving a calculus problem involving the calculation of areas under a curve, integrals, and the determination of concavity and extreme values of a function.
What are the three parts of the problem discussed in the transcript?
-The three parts of the problem discussed are: calculating the value of G(0) and G(4) using integrals, finding the absolute minimum value of G on the closed interval from negative four to four, and determining the intervals where the function G(x) is concave down.
What is the function f(t) representing in the context of the problem?
-The function f(t) represents the function whose integral from negative four to a variable x gives the function G(x), as per the fundamental theorem of calculus.
How is the area of a triangle calculated in the script?
-The area of a triangle is calculated as half the product of its base and height, which in the script is demonstrated with a triangle having a base of 3 and a height of 3, resulting in an area of 9 halves or 4.5 square units.
What is the significance of the points x = -1/2, x = 1/2, and x = 5/2 in the context of the problem?
-The points x = -1/2, x = 1/2, and x = 5/2 are significant as they are the x-values where horizontal tangents to the graph of f(x) are located, indicating potential points of interest in the analysis of the function.
What does the term 'critical points' refer to in calculus?
-In calculus, 'critical points' refer to the points where the derivative of a function is zero or undefined, which often correspond to local maxima, minima, or points of inflection.
How does the script describe the process of finding the absolute minimum value of G(x) on a closed interval?
-The script describes the process as finding the derivative of G(x), setting it to zero to find critical points, and then evaluating G(x) at these points as well as at the endpoints of the interval to determine the absolute minimum value.
What is the role of the second derivative in determining the concavity of a function?
-The second derivative plays a crucial role in determining the concavity of a function. If the second derivative is positive, the function is concave up, and if it is negative, the function is concave down.
What is the significance of points of inflection in the context of the problem?
-Points of inflection are significant in the context of the problem as they are the points where the concavity of the function changes, either from concave up to concave down or vice versa.
How does the script handle the calculation of G(4) involving a complex integral?
-The script breaks down the calculation of G(4) by first using previously found values and then focusing on the remaining integral part, which involves finding the antiderivative of the given function and evaluating it between the limits of integration.
Outlines
📈 Calculating G(0) and G(4) Using Integrals
The paragraph explains the process of calculating the function G at 0 and 4 using definite integrals. It starts with identifying the function's graph and its horizontal tangents at specific x-values. The instructor then calculates G(0) by finding the area under the curve from -4 to 0, which includes a triangle and a negative region, resulting in 1.5 as the final answer. For G(4), the calculation involves breaking the integral into parts, finding antiderivatives, and evaluating them between the limits of integration, leading to a complex arithmetic process.
🔍 Detailed Steps in Calculating G(4) and Error Correction
This paragraph delves deeper into the calculation of G(4), emphasizing the need to find the antiderivative of the given function and evaluate it between the limits of 1 to 4. The instructor makes arithmetic errors during the calculation, which are later corrected by re-evaluating the integral and ensuring the correct application of the limits of integration. The process includes finding the common denominator and simplifying the expression to reach the final value for G(4).
📚 Understanding G'(x) and Finding Absolute Minimum
The focus shifts to understanding the derivative of G(x), which is given by the fundamental theorem of calculus as f(x). The instructor discusses the steps to find absolute minimums and maximums on a closed interval, emphasizing the importance of evaluating the function at critical points and boundaries. The paragraph concludes with the identification of critical points from the graph of f(x) and the process of evaluating G(x) at these points to find the absolute minimum.
📉 Determining the Absolute Minimum Value of G(x)
Building on the previous discussion, the paragraph identifies the process of finding the absolute minimum value of G(x) on the interval from -4 to 0. The instructor uses the graph to determine where the function changes from decreasing to increasing, which indicates a potential absolute minimum. The values of G at -4 and 0 are compared, with G(-4) being zero due to the same limits of integration, and G(0) previously calculated as 1.5, leading to the conclusion that the absolute minimum is at x = -4.
📌 Identifying Concavity and Points of Inflection
The paragraph discusses the concept of concavity and how to determine whether a function is concave up or down by analyzing the second derivative. The instructor explains the process of finding the second derivative from the graph and identifies the intervals where the function is concave up and concave down. Points of inflection, where the concavity changes, are also highlighted, providing a clear understanding of the function's behavior across different intervals.
📋 Summarizing Concavity Intervals for G(x)
The final paragraph wraps up the discussion by summarizing the intervals where the function G(x) is concave down. The instructor lists the intervals as negative 2 to negative 0.5, 0.5 to 1, and 2.5 to 4, based on the analysis of the second derivative from the previous paragraph. This summary provides a clear and concise overview of the function's concavity for easy reference.
Mindmap
Keywords
💡Graph
💡Horizontal Tangents
💡Integral
💡Area Under the Curve
💡Triangle Area
💡Antiderivative
💡Critical Points
💡Absolute Minimum
💡Concave Up/Down
💡Second Derivative
💡Point of Inflection
Highlights
The session covers the solution to a calculus problem involving the graph of a function f, horizontal tangents, and areas under the curve.
The instructor explains how to find the area under a curve using integration, starting with the integral from negative four to zero.
A triangle's area under the curve from negative four to negative one is calculated, demonstrating the use of base and height.
The concept of negative areas under the curve is introduced, with the area from negative one to zero being subtracted from the total.
The instructor simplifies the expression for G of zero by using the given areas A and B, resulting in three halves or 1.5.
The process for finding G of four involves breaking down the integral into pieces and summing the areas.
The integral from negative four to zero is reused, and the next piece from negative one to zero is identified as area B.
The instructor guides students through finding the antiderivative of a given function to calculate the remaining area.
A detailed calculation of the integral from one to four is performed, involving the antiderivative of a quadratic function.
The instructor emphasizes the importance of checking work and using a common denominator for complex calculations.
The concept of absolute minimum value of G is introduced, with a step-by-step approach to finding it on a closed interval.
The fundamental theorem of calculus is applied to find G prime, which is equal to the function f.
Critical points are identified from the graph of f, which are potential candidates for absolute minimum or maximum values.
The instructor explains how to determine whether a function is concave up or down by finding the second derivative.
The process of finding points of inflection, where the function changes from concave up to concave down, is discussed.
The instructor concludes by summarizing the intervals where the function is concave down, providing a clear answer to part C of the problem.
Throughout the session, the importance of understanding calculus concepts such as integration, differentiation, and concavity is emphasized.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: