You wouldn’t expect this "quadratic" equation to have 6 solutions!
TLDRThe video script presents a mathematical exploration of a quadratic equation with an absolute value. The presenter initially suggests that by applying an absolute value to 'x' in a quadratic equation, one might expect to find six solutions, inspired by Michael Jordan's six championships. However, the presenter quickly clarifies that this is not the case and instead embarks on a detailed analysis. They consider the absolute value in two cases: when 'x' is less than zero and when it is non-negative. The script then delves into the possibility of complex solutions, leading to a total of six solutions—two real and four complex. The presenter uses the general form of a complex number (a + bi) and squares it, then isolates and squares both the real and complex parts to find the solutions. After a thorough case-by-case analysis, the presenter concludes with the six solutions to the equation, providing a satisfying and educational experience for viewers interested in the intricacies of quadratic equations and complex numbers.
Takeaways
- 🧮 When solving a quadratic equation with an absolute value around x, it can yield more than the usual two solutions, potentially six, including complex solutions.
- 📐 The absolute value of x can be interpreted as the distance from zero on the number line, which leads to considering both positive and negative scenarios for x.
- 🔍 To address the absolute value, cases are considered separately where x could be negative (leading to -x) or non-negative (remaining as x).
- 🌟 The speaker initially thought the equation might yield six solutions like Michael Jordan's championships, but found that this isn't always the case.
- 📉 The attempt to use the property of absolute value as the square root of x^2 does not consistently yield six solutions, leading to at most four solutions.
- 🤔 To obtain six solutions, the equation must have both real and complex solutions, which requires considering complex numbers in the form a + bi, where a and b are real numbers.
- 🔗 When dealing with the absolute value of a complex number, it is the distance from the origin in the complex plane, calculated as √(a^2 + b^2).
- 🧵 The process involves expanding the equation and separating it into real and imaginary parts to solve for a and b under different cases.
- 📌 The real part of the equation must equate to zero, leading to a quadratic equation in terms of a or b, depending on the case being considered.
- 🤓 Through casework, the solutions for a and b are found, which include both real and imaginary numbers, resulting in the six solutions for x.
- 🎓 The final six solutions for x include two real solutions (when a is ±1 and b is 0), and four complex solutions (with a as 0 and b as ±2 or ±3, including the imaginary unit i).
Q & A
What is the main topic discussed in the video script?
-The main topic discussed in the video script is solving a quadratic equation with an absolute value around the variable x, which leads to six solutions, including both real and complex solutions.
Why does putting an absolute value around x in a quadratic equation result in six solutions?
-Putting an absolute value around x results in six solutions because it creates two cases for x: one where x is non-negative and one where x is negative. This leads to both real and complex solutions when considering the general form of a complex number (a + bi).
What is the general form of a complex number?
-The general form of a complex number is a + bi, where a and b are real numbers, and i is the imaginary unit.
How does the absolute value of a complex number relate to its distance from the origin on the complex plane?
-The absolute value of a complex number is equal to the distance from the origin on the complex plane. It is calculated as the square root of the sum of the squares of the real part (a) and the imaginary part (b), or √(a^2 + b^2).
What are the two real solutions found when a is equal to one or negative one in the equation?
-The two real solutions are ±1, which means the solutions are 1 and -1.
What are the purely imaginary solutions found when a is zero?
-The purely imaginary solutions are ±2i, which means the solutions are 2i and -2i.
How does the video script demonstrate the process of solving for complex solutions?
-The script demonstrates the process by first considering the real and imaginary parts separately, then setting up equations based on these parts being equal to zero. It then solves for the values of a and b under different conditions, leading to the complex solutions.
What is the significance of considering the cases where a is greater than zero, less than zero, and b is greater than zero or less than zero?
-Considering these cases is significant because it allows for a comprehensive analysis of the quadratic equation with an absolute value. It ensures that all possible solutions, including those that are complex, are found.
What is the role of the square root in the context of the absolute value of a complex number?
-The square root is used to calculate the magnitude or modulus of a complex number, which represents the distance from the origin in the complex plane. It is part of the expression √(a^2 + b^2), where a and b are the real and imaginary parts of the complex number, respectively.
How does the video script handle the complexity of the solutions when a and b are both zero?
-When both a and b are zero, the script simplifies the equation to find the real solutions directly, without the need for complex number manipulations.
What is the final count of solutions found for the quadratic equation with an absolute value around x?
-The final count of solutions is six, which includes two real solutions and four complex solutions.
How does the video script use the concept of absolute value to explore the solutions of a quadratic equation?
-The script uses the concept of absolute value to create two separate cases for x, one for when x is non-negative and one for when x is negative. This approach allows for the exploration of both real and complex solutions to the quadratic equation.
Outlines
🔍 Exploring the Impact of Absolute Value on Quadratic Equations
The speaker begins by addressing a quadratic equation and introduces a twist by placing an absolute value around the variable x. This modification surprisingly leads to six solutions, drawing a parallel to Michael Jordan's six championships. The speaker then invites viewers to pause and experiment before diving into the mathematical reasoning. The absolute value is handled by considering two cases based on the definition of absolute value, leading to the conclusion that the initial approach does not yield six solutions. The exploration continues with the idea of representing the absolute value as the square root of x squared, which could potentially lead to four solutions at most. The key insight is that to achieve six solutions, some must be complex. The speaker then generalizes the variable x as a complex number (a + bi), where a and b are real numbers. The equation is expanded and simplified, leading to two conditions that must be met for the real and complex parts. Through casework based on the values of a and b, the speaker systematically solves for the possible values of b and a, eventually identifying the six solutions to the equation, which include two real solutions (±1), two purely imaginary solutions (±2i), and two complex solutions (-2 + 3i and -3 + 2i).
🧮 Solving for the Six Solutions of the Modified Quadratic Equation
Continuing from the previous paragraph, the speaker focuses on solving the equation derived from the complex number representation of x. The equation is split into real and complex parts, each set to zero. For the real part, the speaker solves a quadratic equation in terms of b, considering both cases where b is greater than zero and less than zero, yielding solutions of b = 2 or 3, and b = -2 or -3, respectively. For the complex part, the condition 2a = 0 simplifies to a being either 0 or undefined. Two cases for a are considered: when a is greater than zero, yielding a = 1, and when a is less than zero, which is disregarded as it does not fit the context. When a equals zero, the solutions for b become ±2i, corresponding to purely imaginary solutions. The speaker concludes by summarizing the six solutions: two real solutions at a = ±1 with b = 0, two purely imaginary solutions at a = 0 with b = ±2i, and two complex solutions at a = 0 with b = ±2 or ±3i, thus satisfying the initial quest for six solutions.
Mindmap
Keywords
💡Quadratic Equation
💡Factoring
💡Absolute Value
💡Complex Numbers
💡Case Work
💡Distance in Complex Plane
💡Real Part and Imaginary Part
💡Pythagorean Theorem
💡Squaring
💡Roots of an Equation
💡Michael Jordan
Highlights
Solving a quadratic equation by factoring results in two solutions.
Introducing an absolute value around x in the quadratic equation surprisingly leads to six solutions, similar to Michael Jordan's six championships.
Not all quadratic equations yield six solutions when an absolute value is applied.
Using the property that the absolute value of x equals either -x (when x < 0) or x (when x ≥ 0) to handle the absolute value.
Writing the absolute value of x as the square root of x squared, which can lead to at most four solutions.
To have six solutions, some must be complex - two real solutions and four complex solutions.
Representing x as a complex number in the form a + bi, where a and b are real numbers.
Expanding the equation (a + bi)^2 + 5|a + bi| - 6 = 0 and separating the real and complex parts.
The absolute value of a complex number measures the distance from the origin in the complex plane.
Setting the real part of the equation (a^2 - b^2 + 5√(a^2 + b^2) - 6 = 0) to zero and solving for a and b.
Considering two cases based on the value of a: a = 0 and a ≠ 0.
When a = 0, solving the equation b^2 + 5|b| - 6 = 0 for b, resulting in b = 2, 3, -2, -3.
When a ≠ 0, solving the equation a^2 + 5|a| - 6 = 0 for a, resulting in a = ±1.
The six solutions to the equation are x = ±1 (real), x = ±2i (imaginary), and x = ±3i (imaginary).
The process involves casework based on the signs of a and b, and factoring quadratic equations.
The solution demonstrates the interplay between real and complex numbers in solving a modified quadratic equation.
The creative approach of adding an absolute value to a quadratic equation results in an unexpected number of solutions.
This exploration of the problem showcases the beauty and intricacy of mathematics, leading to a satisfying conclusion.
Transcripts
Browse More Related Video
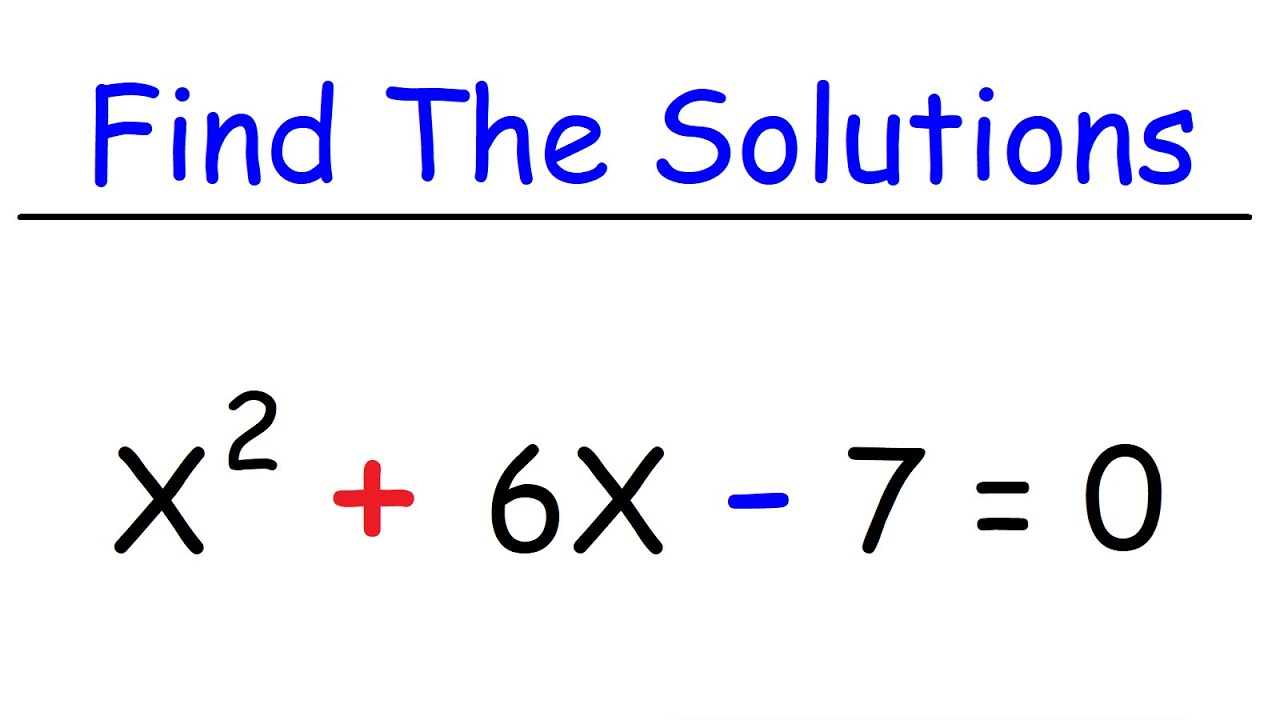
How To Find The Real & Imaginary Solutions of Polynomial Equations
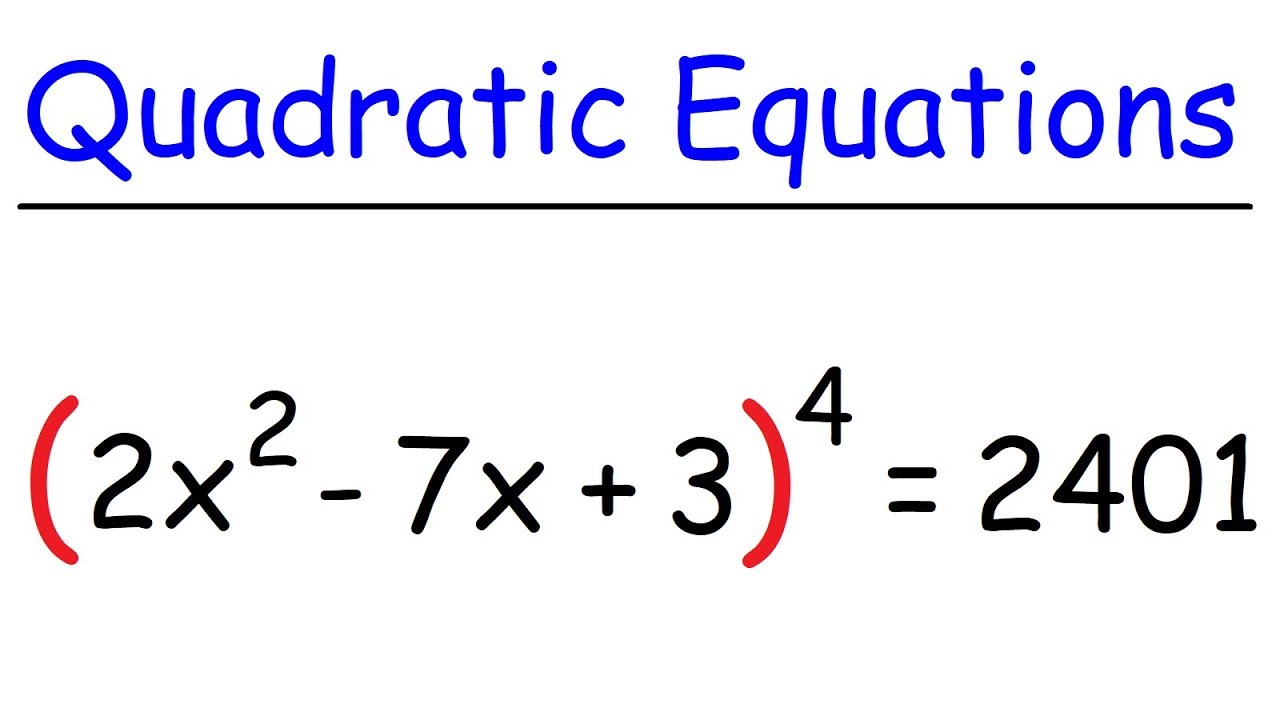
Solving Quadratic Equations With Exponents

EXTREME quintic equation! (very tiring)

Let's Solve A Nice Factorial Equation

An Interesting Trigonometric Equation | Viewer Suggested

Introduction to Complex Solutions of Polynomials (Precalculus - College algebra 35)
5.0 / 5 (0 votes)
Thanks for rating: