Limits! Part 2

Ian Grigsby
12 Jun 201918:36
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video delves into the algebraic aspect of limits, focusing on polynomial and rational functions. It emphasizes the straightforward rule of 'plugging in' the value when dealing with limits of these functions. The video also addresses scenarios where limits do not exist, such as when encountering a nonzero number divided by zero (leading to a vertical asymptote) or an indeterminate form like 0/0 or ∞/∞ (requiring further algebraic manipulation). Additionally, it introduces shortcuts for evaluating limits as X approaches infinity by comparing the degrees of the numerator and denominator, resulting in either infinity, zero, or a ratio of coefficients depending on their relative degrees. The video concludes with practical advice on handling limits and the importance of performing algebraic simplifications to obtain clear results.

Takeaways
  • 📚 **Plug-In Rule for Polynomials**: To find the limit of a polynomial function as X approaches a certain value, simply substitute the value into the function.
  • 🚫 **Division by Zero**: If a rational function results in a division by zero, the limit does not exist, indicating a vertical asymptote.
  • 🔢 **Indeterminate Forms**: An indeterminate form like 0/0 or ∞/∞ suggests that further algebraic manipulation is required to find the limit.
  • ✅ **Cancelling in Rational Functions**: When dealing with indeterminate forms, look for factors that can be cancelled out in the numerator and denominator of a rational function.
  • 🔄 **Simplifying Indeterminate Forms**: After cancelling common factors, revert to the plug-in rule to find the simplified limit.
  • ∞ **Limits at Infinity**: When evaluating limits as X approaches infinity, compare the degrees of the polynomials in the numerator and denominator.
  • ⏫ **Degree of Numerator Greater**: If the degree of the numerator is greater than the denominator, the limit tends to infinity.
  • ⏬ **Degree of Numerator Less**: If the degree of the numerator is less than the denominator, the limit approaches zero.
  • 🔀 **Equal Degrees**: When the degrees are equal, the limit is the ratio of the leading coefficients of the numerator and denominator.
  • 📉 **Zero Divided by Zero**: A limit resulting in 0/0 indicates that algebraic simplification can lead to a determinate value.
  • 📈 **Shortcut for Infinity Limits**: Use the degrees of the polynomials to find the limit as X approaches infinity without full simplification.
Q & A

  • What is the first rule for computing the limit of a polynomial function?

    -The first rule for computing the limit of a polynomial function is to simply plug in the number at which the limit is being evaluated.

  • How does the limit of a rational function behave when the denominator equals zero?

    -If the denominator equals zero, the limit does not exist because it would imply division by zero, which is undefined.

  • What is an indeterminate form and how does it relate to limits?

    -An indeterminate form, such as 0/0 or ∞/∞, indicates that more algebra is required to determine the limit. It suggests that there might be factors that can be canceled out, simplifying the expression.

  • When does the limit of a rational function as X approaches a certain number C result in an indeterminate form 0/0?

    -The limit of a rational function results in an indeterminate form 0/0 when the function, after plugging in the value C, results in a numerator that is zero and a denominator that is also zero.

  • How can you simplify the process of finding the limit as X approaches infinity for a rational function?

    -You can simplify this process by comparing the degrees of the polynomials in the numerator and the denominator. The limit behavior depends on whether the degree of the numerator is greater than, less than, or equal to the degree of the denominator.

  • What is the result of the limit as X approaches infinity for a rational function where the degree of the numerator is greater than the degree of the denominator?

    -In such a case, the limit as X approaches infinity is infinity, or it does not exist, because the function grows without bound as X increases.

  • What is the result of the limit as X approaches infinity for a rational function where the degree of the numerator is less than the degree of the denominator?

    -In this scenario, the limit as X approaches infinity is 0, because the growth of the denominator outpaces the numerator, making the overall function tend towards zero.

  • What happens to the limit as X approaches infinity for a rational function when the degrees of the numerator and the denominator are equal?

    -When the degrees are equal, the limit as X approaches infinity is determined by the ratio of the coefficients of the highest power terms in the numerator and the denominator.

  • Why is it important to factor the numerator and denominator when dealing with an indeterminate form like 0/0 in a rational function?

    -Factoring can reveal common factors that can be canceled out, which simplifies the expression and allows for the application of the basic limit rule of plugging in the value of X.

  • How does the concept of horizontal asymptotes relate to the limit of a rational function as X approaches infinity?

    -The behavior of the limit as X approaches infinity can indicate the presence of a horizontal asymptote. If the limit is a finite number, that number is the value of the horizontal asymptote. If the limit is infinity, there is no horizontal asymptote.

  • What is the general rule for evaluating limits when you encounter a nonzero number divided by zero in a rational function?

    -When you encounter a nonzero number divided by zero, it indicates that the limit does not exist. This situation often corresponds to a vertical asymptote on the graph of the function.

Outlines
00:00
📚 Introduction to Algebraic Limits

This paragraph introduces the concept of algebraic limits, focusing on how to compute limits for polynomial and rational functions when a graph is not available. The key takeaway is that for polynomial functions, one simply substitutes the value of 'C' into the function to find the limit. An example is provided, calculating the limit as X approaches 3 for the function x^2 - 5x, which results in -6. The paragraph also touches on the process for rational functions, emphasizing the importance of ensuring the denominator is not zero to avoid division by zero errors.

05:04
🚫 Limit Does Not Exist Scenarios

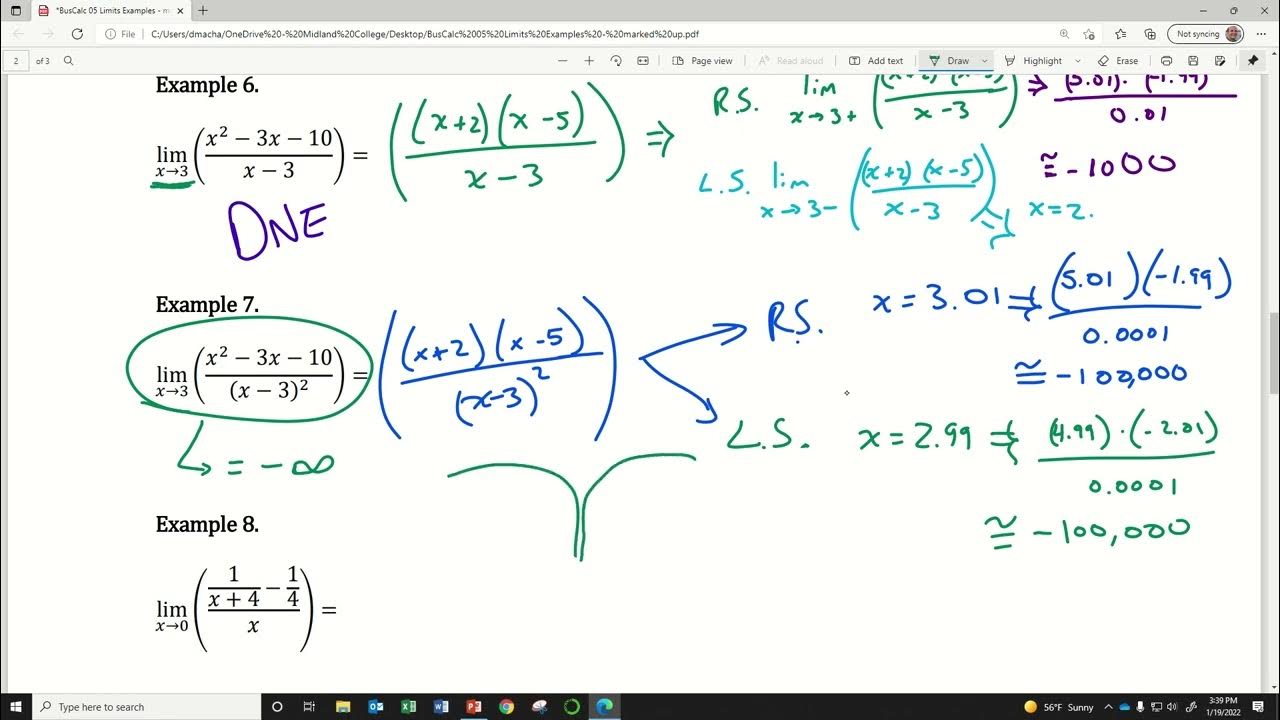
The second paragraph delves into situations where limits do not exist, particularly when dealing with rational functions. It explains that if the denominator equals zero, the limit is undefined, as illustrated by the example of the function (x + 3) / x^2 as X approaches 0, which results in 3/0. The concept of a vertical asymptote is introduced as a graphical representation of such scenarios. The paragraph also discusses indeterminate forms, such as 0/0, which suggests that further algebraic manipulation is required to find the limit. An example of this is the limit as X approaches 5 for the function (x^2 - 25) / (x - 5), which initially results in 0/0 but can be resolved through factoring and simplification.

10:06
🔢 Handling Indeterminate Forms and Infinity

This paragraph addresses how to handle indeterminate forms and limits as X approaches infinity or negative infinity for rational functions. It explains that when faced with an indeterminate form like 0/0, one should perform additional algebraic steps, such as factoring, to simplify the expression. The paragraph also provides shortcuts for evaluating limits at infinity by comparing the degrees of the numerator and denominator. Three scenarios are outlined: if the degree of the numerator is greater than the denominator, the limit is infinity; if the degree of the numerator is less, the limit is zero; and if the degrees are equal, the limit is the ratio of the coefficients of the highest powers.

15:07
🏁 Summary of Limit Evaluation Techniques

The final paragraph summarizes the key points discussed in the video script. It reiterates the initial rule for evaluating limits of polynomial and rational functions by substituting the value directly into the function. It also highlights the conditions under which the limit does not exist, such as when encountering a nonzero number divided by zero or an indeterminate form. The importance of performing algebraic manipulations to resolve indeterminate forms is emphasized, as is the method for evaluating limits as X approaches infinity by examining the degrees of the polynomials involved. The paragraph concludes with advice to practice these techniques and to always write out the limit before evaluating it.

Mindmap
Keywords
💡Limits
Limits are a fundamental concept in calculus that describe the behavior of a function as the input approaches a certain value. In the video, limits are used to analyze functions, particularly polynomials and rational functions, to understand their behavior as the variable approaches specific points or infinity. The script discusses how to compute limits algebraically.
💡Polynomials
Polynomials are expressions consisting of variables and coefficients, involving only the operations of addition, subtraction, and multiplication, and non-negative integer exponents of variables. The video explains that to find the limit of a polynomial function as x approaches a certain value, one simply substitutes the value into the polynomial expression, as demonstrated with the function x^2 - 5x.
💡Rational Functions
Rational functions are ratios of two polynomials. The video discusses how to compute the limit of a rational function by substituting the value into both the numerator and the denominator, provided the denominator does not become zero, which would result in an undefined expression (division by zero).
💡Indeterminate Forms
Indeterminate forms, such as 0/0 or ∞/∞, occur when the direct substitution of a value into a rational function results in a form that does not provide a direct answer. The video emphasizes that an indeterminate form is a signal that further algebraic manipulation is required to simplify the expression and find the limit.
💡Vertical Asymptote
A vertical asymptote is a vertical line that a graph approaches but never crosses. In the context of the video, a vertical asymptote is mentioned when discussing what happens when the limit involves division by zero, which is undefined. The script uses the example of the function (x + 3)/(x^2) as x approaches zero to illustrate this concept.
💡Factoring
Factoring is the process of breaking down a polynomial into its factors, which are simpler polynomials that when multiplied together give the original polynomial. The video demonstrates that factoring can help resolve indeterminate forms by canceling out common factors in the numerator and the denominator, as shown with the function x^2 - 25/(x - 5).
💡Horizontal Asymptotes
Horizontal asymptotes are horizontal lines that a graph approaches as the function's input (x) approaches infinity or negative infinity. The video provides rules for determining horizontal asymptotes by comparing the degrees of the numerator and the denominator in a rational function.
💡Degrees of Polynomials
The degree of a polynomial is the highest power of the variable in the polynomial. In the video, the degree is used to determine the behavior of the limit as x approaches infinity for rational functions. The script explains that if the degree of the numerator is greater than the degree of the denominator, the limit is infinity, and if it is less, the limit is zero.
💡Algebraic Manipulation
Algebraic manipulation involves performing operations on algebraic expressions to simplify them or to make them easier to solve. The video emphasizes the importance of algebraic manipulation in finding limits, especially when dealing with indeterminate forms, by factoring and canceling common terms.
💡Plug-in Method
The plug-in method is a straightforward technique for finding the limit of a function by substituting the value of the variable that the function approaches directly into the function. The video uses this method as a primary rule for calculating limits for polynomial and rational functions, as long as the denominator does not become zero.
💡Infinity
In mathematics, infinity is not a number but rather a concept that represents an unbounded quantity. The video discusses how to handle limits as x approaches infinity for rational functions by examining the degrees of the polynomials in the numerator and the denominator and using this information to find horizontal asymptotes.
Highlights

Introduction to algebraic limits and their computation

Discussion on limits of polynomial functions by plugging in the value

Explanation of limits for rational functions and the rule of plugging in the value

Condition when the denominator equals zero, leading to a limit that does not exist

Example of a limit that does not exist due to division by zero

Introduction to indeterminate forms such as 0/0 and infinity/infinity

How to handle indeterminate forms by performing further algebra

Explanation of limits as X approaches infinity or negative infinity for rational functions

Shortcut for evaluating limits as X approaches infinity based on the degree of numerator and denominator

Three scenarios for evaluating limits as X approaches infinity based on the degrees of the numerator and denominator

Method for finding horizontal asymptotes using the degrees of the numerator and denominator

Rule for when the degree of the numerator is greater than the denominator

Rule for when the degree of the numerator is less than the denominator

Rule for when the degrees of the numerator and denominator are equal

Summary of the main rules for evaluating limits of polynomial and rational functions

Advice on writing out the limit process and the importance of plugging in the number

Transcripts

Browse More Related Video

Using L'Hopital's Rule to show that exponentials dominate polynomials

Calculus: Limits at Infinity-Algebraic

Limits via Graphs!

Introduction to l'Hôpital's rule | Derivative applications | Differential Calculus | Khan Academy

BusCalc 05 Limits Examples Pt 2

Finding a Horizontal Asymptote of a Rational Function (Precalculus - College Algebra 40)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsLimitsPolynomialsRational FunctionsIndeterminate FormsAsymptotesAlgebraic TechniquesEducational ContentCalculusLimit EvaluationVertical Asymptote