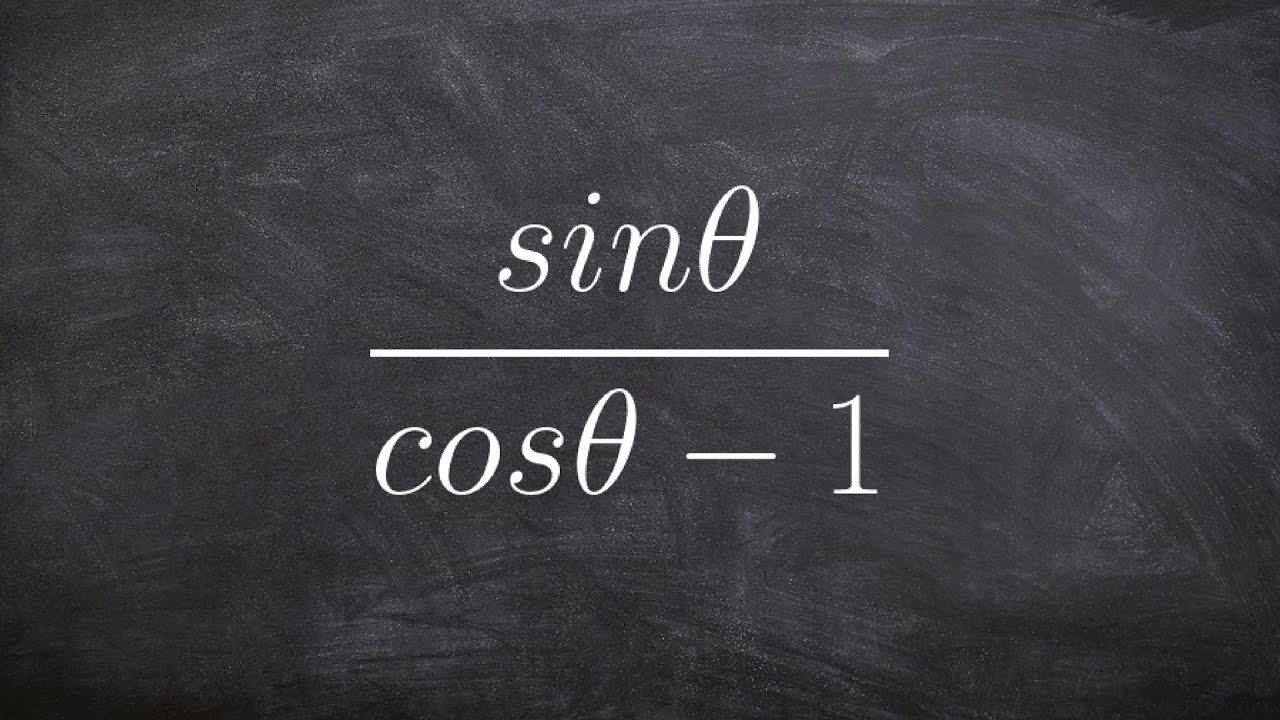Verifying trigonometric identities, hard with multiple steps
TLDRThe video script is a detailed walkthrough of a trigonometric identity simplification problem. The presenter starts by choosing to work on the left side of the identity, which they believe is already simplified. They then apply operations to the expression, ensuring common denominators, and proceed to simplify the numerator by distributing and rewriting terms. The presenter uses the Pythagorean identity (cosine squared plus sine squared equals 1) to further simplify the expression. Eventually, they multiply by the reciprocal to eliminate the denominator and end up with an expression involving cosecant of theta. The presenter emphasizes the importance of combining terms with common denominators and encourages viewers to follow each step carefully to understand the process fully.
Takeaways
- 📐 The problem involves simplifying an identity with trigonometric functions, specifically focusing on the left side of the equation as it's already simplified.
- 🔍 The first step is to apply operations to the left side of the equation, which includes multiplying by the denominator to ensure common denominators.
- 🧮 After ensuring common denominators, the next step is to simplify the numerator by distributing the negative one and rewriting cotangent as cosine over sine.
- ✅ The goal is to simplify the expression to resemble a known trigonometric identity, in this case, cosecant squared of theta.
- 🔄 The process involves combining terms with the same denominator, which is sine in this case, to simplify the numerator further.
- 🤔 The realization that cosine squared plus sine squared equals 1 is key to simplifying the expression and eliminating terms.
- 📉 The simplified numerator ends up being 1 minus sine of theta over sine of theta, which is then divided by 1 minus sine of theta.
- 🤓 A mistake is acknowledged, and it's corrected to 1 over sine of theta, which is the reciprocal of the denominator, leading to the final form of cosecant of theta.
- 🚫 The speaker emphasizes the importance of combining terms with like denominators and the need to keep combining and adding them up.
- 💡 The final recommendation is to focus on combining terms and getting the denominator off to simplify the expression successfully.
- ❓ The speaker invites questions and acknowledges the complexity of the problem, encouraging students to follow each step carefully.
Q & A
Why is the left side of the identity considered the ideal side to simplify?
-The left side is considered the ideal side to simplify because it is already in a relatively simplified form compared to the right side, which is in terms of cosecant.
What operation is applied to the left side of the identity initially?
-The initial operation applied is multiplying the cosine of theta times cotangent of theta and then subtracting it by one, ensuring to have a common denominator.
How is the common denominator ensured when performing the subtraction?
-The common denominator is ensured by multiplying both the numerator and the denominator by (1 - sine of theta).
What is the purpose of rewriting cotangent as cosine over sine?
-Rewriting cotangent as cosine over sine helps to simplify the numerator by expressing all terms with a common denominator, which in this case is sine of theta.
How does the expression 'cosine squared plus sine squared equals 1' help in simplifying the numerator?
-This expression allows the terms cosine squared and sine squared to be combined and simplified to 1, which simplifies the overall numerator.
What is the final form of the numerator after simplification?
-The final form of the numerator is '1 - sine of theta' divided by 'sine of theta'.
How is the denominator '1 - sine of theta' removed from the expression?
-The denominator is removed by multiplying both the numerator and the denominator by its reciprocal, which is '1 over (1 - sine of theta)'.
What is the final result of the expression after removing the denominator?
-After removing the denominator, the expression simplifies to 'cosecant of theta'.
Why is it important to combine terms with the same denominator?
-Combining terms with the same denominator is crucial for simplifying fractions and making it easier to perform further operations or to see the underlying relationships between different terms.
What does the speaker recommend for dealing with complex expressions like the one in the script?
-The speaker recommends combining terms with like denominators, continuously combining and adding them up, and then addressing the denominator to simplify the expression.
Why might the process described in the script be difficult to follow?
-The process might be difficult to follow due to the multiple steps involved, the need for precise algebraic manipulations, and the complexity of the trigonometric functions used.
What is the significance of the identity being solved in the script?
-The identity being solved is significant as it demonstrates the relationship between different trigonometric functions and their respective identities, which is fundamental in trigonometry.
Outlines
🧮 Simplifying Trigonometric Expressions
The speaker begins by addressing the audience and stating the goal of simplifying a given trigonometric identity. They suggest focusing on the left side of the equation, which they believe is already simplified. The operation involves cosine of theta times cotangent of theta over one minus sine theta, and then subtracting one. To maintain common denominators, the speaker multiplies by one minus sine theta on both the top and bottom. The result is an expression with a common denominator of one minus sine theta squared. The speaker then works on simplifying the numerator by distributing the negative one and rewriting cotangent as cosine over sine. This leads to an expression involving cosine squared theta over sine theta, minus sine theta over sine theta, plus sine squared theta over sine theta. The goal is to simplify and combine these terms, ultimately aiming to get an expression that resembles the cosecant function. The process involves combining terms with the same denominator and using trigonometric identities to simplify further.
🔍 Further Simplification and Final Steps
The speaker continues with the simplification process by addressing the need to get rid of the denominator to make the expression resemble cosecant. They propose multiplying by the reciprocal of the denominator, which is one over one minus sine of theta. This step effectively cancels out the denominator, leaving one over sine of theta, which is the cosecant of theta. The speaker acknowledges the complexity of the problem and advises the audience to ensure they are combining terms with like denominators. They emphasize the importance of continuous combination and addition of terms to eventually isolate the denominator. The speaker concludes by seeking questions from the audience to clarify any confusing steps and reiterates the importance of combining terms and simplifying the expression to reach the final form.
Mindmap
Keywords
💡Identity
💡Simplify
💡Cosine
💡Cotangent
💡Sine
💡Denominator
💡Numerator
💡Reciprocal
💡Cosecant
💡Distribute
💡Pythagorean Identity
Highlights
The transcript discusses solving an identity by simplifying the left side, which is already mostly simplified.
Applying operations involves multiplying by (1 - sine theta) on the top and bottom to get a common denominator.
The resulting expression is cosine of theta times cotangent of theta minus (1 - sine theta) over (1 - sine theta squared).
Simplifying the numerator involves distributing the negative sign and rewriting cotangent as cosine over sine.
The numerator is further simplified by combining all terms with a common denominator of sine.
The resulting expression is cosecant squared of theta minus sine squared theta plus sine squared theta over sine of theta.
Using the identity cosine squared plus sine squared equals 1, the expression simplifies to 1 minus sine of theta over sine of theta.
The final simplified form is 1 over sine of theta, which equals cosecant of theta.
The key steps involve applying operations, simplifying the numerator, and eliminating terms using identities.
The process requires careful attention to combining terms with common denominators and simplifying expressions.
The speaker emphasizes the importance of following each step carefully to ensure the correct solution is obtained.
The transcript provides a detailed, step-by-step approach to solving the identity, making it accessible to learners.
The use of visual aids and interactive questioning helps clarify the process and engage the audience.
The speaker's approach emphasizes the importance of understanding the underlying concepts and techniques, rather than just memorizing formulas.
The transcript provides a valuable resource for learners studying trigonometric identities and their applications.
The detailed explanation of each step helps build a strong foundation in trigonometry and problem-solving skills.
The transcript demonstrates the power of combining algebraic manipulation with trigonometric identities to solve complex problems.
The speaker's patient, methodical approach makes the material more approachable for learners at all levels.
The transcript provides a comprehensive guide to solving this particular identity, but the techniques can be applied to other problems as well.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: