13.2a Gravitational Field Strength Theory | A2 G-fields | Cambridge A Level Physics
TLDRThis educational video script delves into the concept of gravitational fields, building upon the understanding of Newton's law of gravitation. The video aims to guide viewers through deriving the equation for gravitational field strength, explaining its significance, and applying it to solve problems. It uses the idea of a test mass to illustrate how the strength of the gravitational field increases as one gets closer to a massive object like a planet. The script also clarifies why the gravitational field strength, denoted by 'g', is approximately constant near the Earth's surface, with a value of 9.81 m/s². This constant value is derived from the simplification that at the Earth's surface, the height above the surface is much smaller compared to the Earth's radius, making it negligible in calculations. The video concludes with a thought-provoking question about the behavior of gravitational field strength inside the Earth and a teaser for a future discussion on this topic. It emphasizes the importance of understanding not just the equation, but also the underlying physics and its practical applications.
Takeaways
- 📘 The concept of gravitational field strength is introduced, analogous to electric fields with field lines and arrows representing direction and magnitude.
- 🔍 Gravitational field strength is derived from Newton's law of gravitation, focusing on the force per unit mass (g = F/M).
- 🌐 The gravitational field strength around a massive object like Earth is visualized in 3D, with arrows pointing towards the center and increasing in size as one gets closer.
- 📈 The equation for gravitational field strength is g = GM/r^2, where G is the gravitational constant, M is the mass of the object, and r is the distance from the center of the mass.
- 🌍 At the Earth's surface, the gravitational field strength is approximately constant, with a value of 9.81 m/s^2, which is the acceleration due to gravity.
- 📊 The unit of gravitational field strength is newtons per kilogram (N/kg), which is equivalent to meters per second squared (m/s^2).
- 🚀 The gravitational field strength decreases with the square of the distance from the center of the mass (an inverse square relationship).
- 🌅 For objects near the Earth's surface, the height (h) is much smaller compared to the Earth's radius (r), so the field strength can be approximated as g = GM/R^2, where R is the Earth's radius.
- 🌍 The Earth's gravitational field is almost uniform near the surface, but it will vary slightly at different heights or radii from the center.
- 📉 The gravitational field strength does not go to zero even as one moves far away from the Earth; it continues to decrease according to the inverse square law.
- 🕳️ A thought experiment is presented: considering the gravitational field strength inside the Earth, questioning whether it would remain constant, increase, or decrease as one moves towards the center of the Earth.
Q & A
What is the primary focus of this chapter?
-The primary focus of this chapter is to understand gravitational fields, specifically gravitational field strength, how to derive the equation for it, and how it applies to various scenarios.
How is the gravitational field strength represented visually?
-The gravitational field strength is visually represented by arrows, where the length of the arrow indicates the strength of the field and the direction of the arrow indicates the direction of the gravitational force.
What is the relationship between the gravitational field strength and the distance from the object generating the field?
-The gravitational field strength is inversely proportional to the square of the distance from the object generating the field. As you move closer to the object, the field strength increases, and as you move further away, the field strength decreases.
What is the equation for calculating gravitational field strength?
-The equation for calculating gravitational field strength is $g = \frac{F_{g}}{m} = \frac{G \cdot m_1 \cdot m_2}{r^2}$, where $g$ is the gravitational field strength, $F_{g}$ is the gravitational force, $m_1$ and $m_2$ are the masses involved, $G$ is the gravitational constant, and $r$ is the distance between the centers of the two masses.
Why is the value of g constant on the Earth's surface?
-The value of g is approximately constant on the Earth's surface because the Earth is a large object and the variation in height (h) is very small compared to the Earth's radius (r). This makes the term $h^2$ negligible compared to $r^2$, leading to a nearly constant value for g at the surface.
What is the unit of gravitational field strength?
-The unit of gravitational field strength is newtons per kilogram (N/kg), which is equivalent to meters per second squared (m/s^2) due to the relationship between force, mass, and acceleration.
What is the value of g near the Earth's surface?
-The value of g near the Earth's surface is approximately 9.81 m/s^2.
How does the gravitational field strength change as you move inside the Earth?
-The script poses a question about the behavior of gravitational field strength as one moves inside the Earth, suggesting that the reader should consider how the field strength might change at different points within the planet.
What does the graph of gravitational field strength (g) versus the square of the distance (r^2) look like?
-The graph of gravitational field strength (g) versus the square of the distance (r^2) would show an inverse square relationship, with g being proportional to 1/r^2. This means that as r^2 increases, the value of g decreases, and the graph would resemble a hyperbolic curve.
How is the gravitational field strength calculated for an object near the surface of a planet like Earth?
-For an object near the surface of a planet like Earth, the gravitational field strength is calculated using the formula $g = \frac{G \cdot M_{\text{earth}}}{r^2}$, where $M_{\text{earth}}$ is the mass of the Earth and $r$ is the distance from the center of the Earth, which for objects near the surface can be approximated as the Earth's radius plus a small height (h).
What happens to the gravitational field strength as you move further away from the Earth?
-As you move further away from the Earth, the gravitational field strength decreases due to the inverse square relationship. The value of g becomes smaller as the distance (r) increases, following the equation $g \propto \frac{1}{r^2}$.
Outlines
📘 Introduction to Gravitational Fields
This paragraph introduces the concept of gravitational fields, building upon previous discussions on Newton's law of gravitation. It emphasizes the importance of understanding gravitational field strength, which is likened to electric fields in terms of its representation through field lines and arrows. The video aims to teach viewers how to derive the equation for gravitational field strength and solve problems using this equation. Additionally, it touches on the constancy of 'g' on Earth's surface and its significance.
🧮 Deriving the Gravitational Field Strength Equation
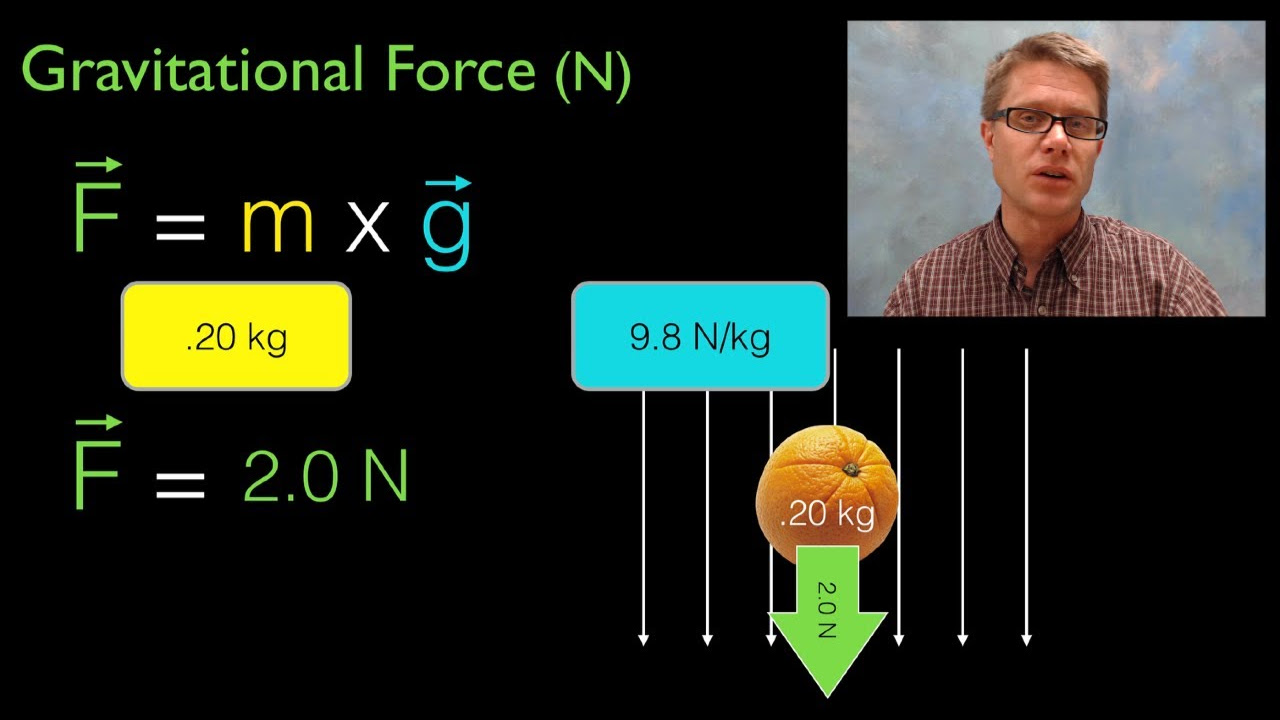
The paragraph focuses on deriving the equation for gravitational field strength using Newton's law of gravitation. It explains that the strength of the gravitational field (g) at a point is defined as the force per unit mass. The derivation process involves using the gravitational force equation (F = G * (m1 * m2) / r^2) and simplifying it to find g = G * m1 / r^2, where m1 is the mass of the larger body (like Earth), r is the distance between the centers of the two masses, and G is the gravitational constant. The unit of gravitational field strength is also discussed, revealing it to be newtons per kilogram or meters per second squared, which is related to acceleration.
🌍 Gravitational Field Strength at Earth's Surface
This section delves into the specifics of gravitational field strength at Earth's surface. It explains how to calculate the gravitational field strength using the derived equation with Earth's mass (m_e) and radius (r). The concept of 'h', representing height or distance above Earth's surface, is introduced. The simplification for near-surface calculations is discussed, where the height (h) is considered negligible compared to Earth's radius (r), leading to a constant value for 'g' at Earth's surface (approximately 9.81 m/s^2). A simulation is referenced to illustrate the calculation and confirm the familiar value of Earth's surface gravity.
📊 Gravitational Field Strength vs. Distance
The paragraph explores the relationship between gravitational field strength (g) and distance (r) from a massive object like Earth. It explains that as one moves further away, the gravitational field strength weakens, inversely proportional to the square of the distance (1/r^2). The concept of a uniform gravitational field near Earth's surface is introduced, emphasizing the near-parallel field lines and the constant value of 'g' at the surface. The paragraph concludes with a thought-provoking question about what happens to the gravitational field strength inside Earth and invites viewers to consider the graphical representation of g vs. r.
🚀 Applying Theory: Examples and Further Questions
In the final paragraph, the focus shifts to applying the theoretical concepts discussed earlier. The video intends to provide examples to reinforce understanding and problem-solving skills regarding gravitational field strength. It also poses a final question to ponder about the behavior of gravitational field strength inside the Earth, encouraging viewers to think about the implications of the 1/r^2 relationship in such a scenario before揭晓 the answer in a subsequent video.
Mindmap
Keywords
💡Gravitational Field Strength
💡Newton's Law of Gravitation
💡Test Mass
💡Gravitational Force
💡Simulation
💡Field Vector
💡Uniform Field
💡Inverse Square Law
💡Acceleration
💡Surface of the Earth
Highlights
Gravitational field strength is introduced as a concept similar to the electric field, with fields represented by lines and arrows.
The focus of the lesson is on understanding and deriving the equation for gravitational field strength.
A simulation of a 3D gravitational field around a sphere is shown, illustrating how field strength varies with distance from the center.
The concept of a test mass is used to define the gravitational field strength at a point.
The equation for gravitational field strength is derived using Newton's law of gravitation and the force per unit mass.
The unit of gravitational field strength is newtons per kilogram (N/kg), which is equivalent to meters per second squared (m/s^2).
The gravitational field strength at the Earth's surface is shown to be constant, with a value of approximately 9.81 m/s^2.
The relationship between gravitational field strength and the distance from the center of a mass is inversely proportional to the square of the distance (1/r^2).
A graphical representation of gravitational field strength versus distance is discussed, showing how the field strength decreases with increasing distance.
The concept of a uniform gravitational field is introduced, explaining why the field strength is constant near the Earth's surface.
The derivation of the gravitational field strength equation is emphasized as an important concept to understand for exams.
The lesson touches on the practical application of understanding gravitational field strength for solving problems related to gravitational forces.
A thought experiment is presented, asking what would happen to the gravitational field strength if one were to go inside the Earth.
The lesson concludes with a series of examples to apply the derived equation for gravitational field strength.
The importance of understanding the derivation process of the gravitational field strength equation is stressed for comprehensive knowledge.
The lesson provides a clear and detailed explanation of the concept of gravitational field strength, making it accessible for learners.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: