Gravitational Potential Energy - Introductory Example Problems
TLDRThe video script demonstrates how to calculate gravitational potential energy using two examples. The first example involves a 20 kg suitcase raised 3 meters, resulting in 588 Joules of potential energy. The second example requires finding the mass of an i-beam given its potential energy (108,486 Joules) and height (30 meters), which calculates to a mass of 369 kg. These examples effectively illustrate the application of the formula for gravitational potential energy, PE = mgh.
Takeaways
- 📚 The concept of gravitational potential energy is introduced in the context of physics problems.
- 🧳 A 20 kg suitcase raised 3 meters above the ground is used as an example to explain gravitational potential energy.
- 🔧 The absence of a spring in the example indicates that the potential energy discussed is of the gravitational type.
- 📈 The formula for gravitational potential energy is given as PE = mgh, where m is mass, g is the acceleration due to gravity, and h is height.
- 🪓 The potential energy of the suitcase is calculated to be 588 joules using the provided formula and given values.
- 🏗️ Another example involves an i-beam lifted by a crane to a height of 30 meters with a given potential energy of 108,400 joules.
- 🔄 The potential energy value is used to calculate the mass of the i-beam by rearranging the gravitational potential energy formula.
- 📊 The mass of the i-beam is found to be 369 kg by dividing the total potential energy by the product of gravity and height.
- 📝 The process demonstrated involves substitution of known values into the gravitational potential energy formula to solve for the unknown variable.
- 🎯 The importance of correctly identifying the type of potential energy (gravitational or elastic) is emphasized to solve problems accurately.
- 📌 The examples provided illustrate the practical application of the gravitational potential energy formula in real-world scenarios.
Q & A
What is the concept of gravitational potential energy discussed in the script?
-Gravitational potential energy refers to the energy an object possesses due to its position in a gravitational field, typically as a result of being lifted to a certain height above the ground.
How can you determine if a problem is about gravitational potential energy?
-A problem is about gravitational potential energy if it involves an object being raised to a certain height above the ground and the force being considered is gravity, with no mention of elastic forces or springs.
What are the key components needed to calculate gravitational potential energy?
-To calculate gravitational potential energy, you need the mass of the object (M), the gravitational acceleration (g, which is approximately 9.8 m/s^2 on Earth), and the height above the ground (H).
What is the formula for calculating gravitational potential energy?
-The formula for calculating gravitational potential energy is PE = M * g * H, where PE is the potential energy, M is the mass, g is the gravitational acceleration, and H is the height.
What is the unit of measurement for gravitational potential energy?
-Gravitational potential energy is measured in joules (J).
In the example with the 20-kilogram suitcase, what is the calculated potential energy?
-For the 20-kilogram suitcase raised 3 meters above the ground, the calculated gravitational potential energy is 588 joules (using the formula PE = M * g * H, with M = 20 kg, g = 9.8 m/s^2, and H = 3 m).
In the second example with the i-beam, what is the given potential energy and how can you use it to find the mass?
-The given potential energy for the i-beam is 108,486 joules. Using the formula for gravitational potential energy (PE = M * g * H), and knowing the height (H = 30 m) and the potential energy (PE = 108,486 J), you can solve for the mass (M) by rearranging the formula to M = PE / (g * H).
What is the calculated mass of the i-beam in the second example?
-The calculated mass of the i-beam is 369.48 kilograms, found by dividing the given potential energy (108,486 J) by the product of gravitational acceleration (9.8 m/s^2) and height (30 m).
How does the absence of a spring in the first example indicate that it's a gravitational potential energy problem?
-The absence of a spring suggests that the problem is related to gravity and not elastic potential energy, as springs are associated with elastic deformation and the storing of elastic potential energy.
What is the significance of the height in calculating gravitational potential energy?
-The height is significant because it represents the position of the object in the gravitational field. The higher the object, the greater the work done against gravity, and thus, the greater the gravitational potential energy.
Why is the value of gravitational acceleration constant in these calculations?
-The value of gravitational acceleration (g) is considered constant (approximately 9.8 m/s^2) near the Earth's surface because it represents the acceleration due to Earth's gravity, which is consistent across calculations unless dealing with other celestial bodies with different gravitational pulls.
How can the concepts from the script be applied to real-world scenarios?
-The concepts can be applied to various real-world scenarios such as calculating the energy needed to lift heavy machinery, assessing the potential energy of water stored in a dam, or understanding the energy changes during the launch of a rocket.
Outlines
📚 Gravitational Potential Energy Calculation
This paragraph introduces the concept of gravitational potential energy and explains how to calculate it using the formula PE = mgh, where m is mass, g is the acceleration due to gravity, and h is the height. The speaker uses a practical example of a 20 kg suitcase raised 3 meters above the ground to demonstrate the calculation. They also discuss the absence of a spring in the scenario, confirming that it's gravitational potential energy being discussed. The example is worked out, resulting in a potential energy of 588 joules.
🏗️ Solving for Mass Using Gravitational Potential Energy
The second paragraph presents a different problem involving the calculation of gravitational potential energy. Here, an I-beam is lifted by a crane to a height of 30 meters, and the potential energy is given as 108,486 joules. The speaker explains the process of solving for the unknown mass using the formula for gravitational potential energy. By rearranging the formula and substituting the known values, the speaker calculates the mass of the I-beam to be 369 kilograms. This example further illustrates the application of the gravitational potential energy formula in practical scenarios.
Mindmap
Keywords
💡Gravitational Potential Energy
💡Mass
💡Height
💡Acceleration Due to Gravity (g)
💡Formula
💡Physics Problems
💡Calculation
💡Joules
💡Lifting
💡Energy
Highlights
The concept of gravitational potential energy is introduced in the context of solving physics problems.
A 20 kilogram suitcase is raised 3 meters above the ground as an example scenario for calculating gravitational potential energy.
The absence of a spring in the example indicates that the problem is related to gravitational, not elastic potential energy.
The formula for gravitational potential energy is given as PE = mgh, where m is mass, g is the acceleration due to gravity, and h is height.
The calculation of the suitcase's potential energy results in 588 joules, using the provided mass and height values.
A second problem involves a crane lifting an I-beam to a height of 30 meters, with a given potential energy of 108,486 joules.
The potential energy due to gravity formula is rearranged to solve for the mass of the I-beam.
By dividing the given potential energy by the product of gravity and height, the mass of the I-beam is calculated.
The calculated mass of the I-beam is 369 kilograms.
The process demonstrated is a practical application of the gravitational potential energy formula in real-world scenarios.
The examples show how to approach and solve problems involving gravitational potential energy through systematic calculations.
The importance of correctly identifying the type of potential energy (gravitational or elastic) is emphasized to solve problems accurately.
The use of the constant gravitational acceleration value (9.8 m/s^2) is highlighted as a key factor in these calculations.
The method for calculating potential energy is applicable to various objects, such as suitcases and I-beams, demonstrating its versatility.
The problem-solving approach involves substituting known values into the formula and performing straightforward arithmetic to find the unknown.
The examples serve as a tutorial for students or individuals learning about gravitational potential energy and its calculations.
The transcript provides a clear and detailed explanation of the steps involved in solving physics problems related to gravitational potential energy.
Transcripts
Browse More Related Video

Gravitational Potential Energy Calculations (GPE) - Mass x Gravity x Height OR GPE=mgh

Calculating gravitational potential energy | Modeling energy | High school physics | Khan Academy
Kinetic Energy - Introductory Example Problems

Potential and Kinetic Energy | #aumsum #kids #science #education #children

Elastic Potential Energy - Introductory Example Problems
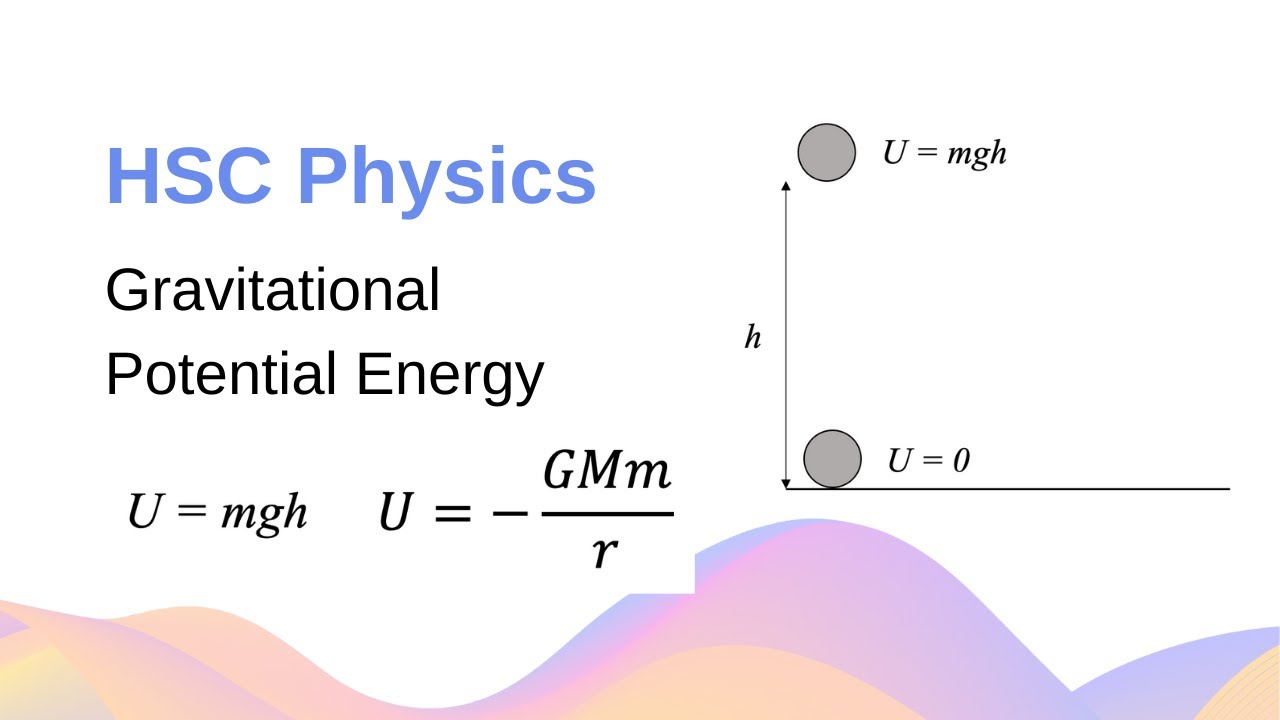
Gravitational Potential Energy & Work Done + Calculation Example // HSC Physics
5.0 / 5 (0 votes)
Thanks for rating: