7.2.3 Matrix Multiplication

Justin Backeberg
1 Apr 202009:58
EducationalLearning
32 Likes 10 Comments

TLDRThis video script delves into the concepts of matrix multiplication, focusing on scalar and row by column multiplication. It explains that scalar multiplication involves distributing a real number across every entry of a matrix, while row by column multiplication requires compatible matrix orders for execution. The script provides step-by-step examples to illustrate how to perform these operations, emphasizing the importance of matching the number of columns in the first matrix with the number of rows in the second to enable multiplication. The video concludes by highlighting that reversing the order of matrices affects the feasibility of multiplication.

Takeaways
  • 🎵 The video begins with an introduction to matrix multiplication, highlighting that there are two types: scalar multiplication and matrix multiplication.
  • 🔢 In scalar multiplication, a real number (scalar) K is multiplied by every entry in matrix A to obtain a new matrix.
  • 🤔 For matrix multiplication to occur, the number of columns in the first matrix (A) must match the number of rows in the second matrix (B).
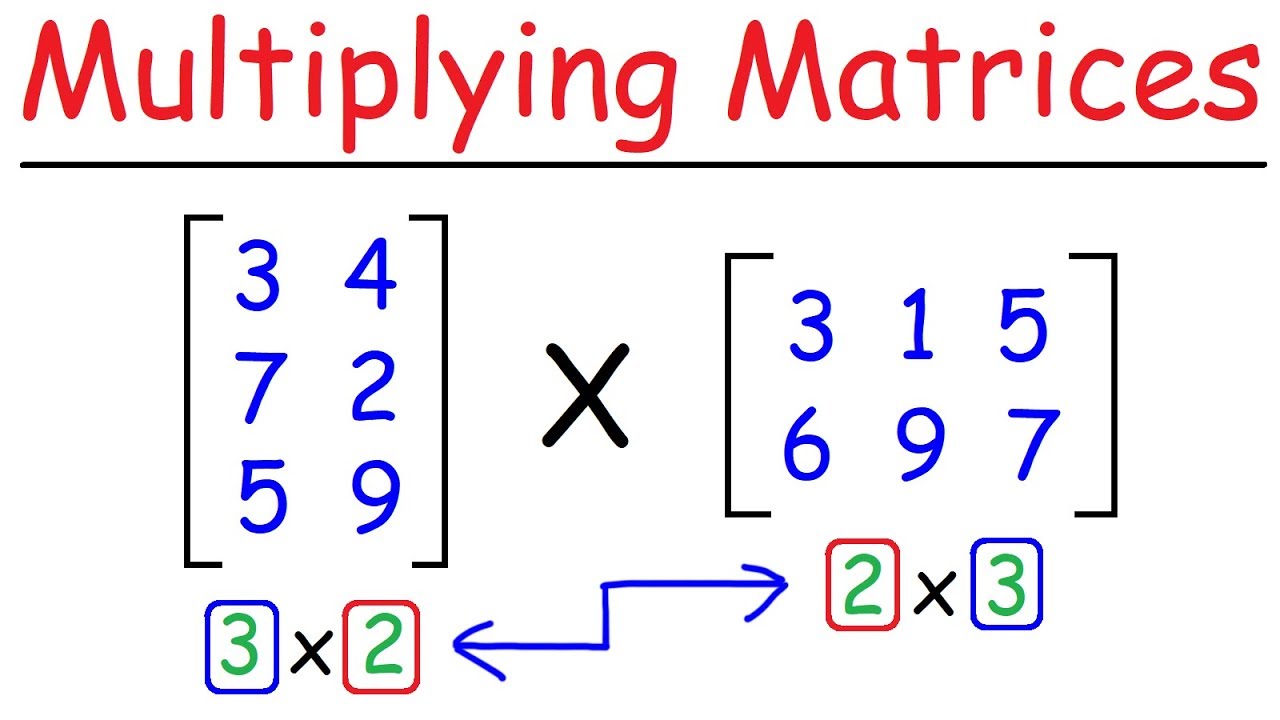
  • 🟫 The order of matrices is described by MxN, where M represents the number of rows and N the number of columns.
  • 🔄 Matrix multiplication involves row-by-column multiplication, where elements from the rows of the first matrix are multiplied with elements from the columns of the second matrix.
  • 🌈 The video provides a color-coded example of multiplying a 2x3 matrix by a 3x2 matrix, resulting in a new 2x2 matrix.
  • 📌 The process of matrix multiplication is demonstrated with a step-by-step calculation, emphasizing the distributive property applied to matrix entries.
  • 🔄 Another example is given where a 2x2 matrix is multiplied by a 2x3 matrix, resulting in a 2x3 matrix.
  • ❌ Swapping the order of matrix multiplication is not always possible; if the middle numbers of the matrices' orders do not match, the multiplication cannot be performed.
  • 📊 The final result of matrix multiplication depends on the orders of the matrices involved, with the outer numbers determining the order of the resulting matrix.
  • 🙏 The video concludes by thanking viewers for their attention and participation.
Q & A

  • What are the two types of matrix multiplication discussed in the video?

    -The two types of matrix multiplication discussed in the video are scalar multiplication and matrix multiplication.

  • What is scalar multiplication in the context of matrices?

    -Scalar multiplication is the process of multiplying each individual entry of a matrix by a real number, known as the scalar.

  • How do you perform scalar multiplication on a matrix?

    -To perform scalar multiplication, you multiply every element in the matrix by the given scalar value.

  • What is required for two matrices to be multiplied together?

    -For two matrices to be multiplied together, the number of columns in the first matrix must be equal to the number of rows in the second matrix.

  • What is the term used for multiplying rows of one matrix by columns of another in matrix multiplication?

    -The process of multiplying rows of one matrix by columns of another matrix is called row by column multiplication.

  • How does the order of matrices affect their multiplication?

    -The order of matrices, specifically the number of rows and columns, determines whether matrix multiplication is possible and also dictates the order of the resulting matrix.

  • What happens when you switch the order of the matrices in multiplication?

    -Switching the order of the matrices in multiplication may result in the multiplication not being possible if the number of columns of the first matrix does not match the number of rows of the second matrix. Even if multiplication is possible, the order of the resulting matrix will be different.

  • How does the size of the resulting matrix change when you multiply two matrices?

    -The size of the resulting matrix is determined by the number of rows from the first matrix and the number of columns from the second matrix.

  • Can you multiply a 2x3 matrix by a 3x2 matrix? What about a 3x2 matrix by a 2x3 matrix?

    -You can multiply a 2x3 matrix by a 3x2 matrix because the number of columns in the first (3) matches the number of rows in the second (3). However, you cannot multiply a 3x2 matrix by a 2x3 matrix because the middle numbers do not match.

  • What is the resulting order of the matrix when a 2x3 matrix is multiplied by a 3x2 matrix?

    -The resulting matrix order when a 2x3 matrix is multiplied by a 3x2 matrix is 2x2.

  • How does the distributive property relate to scalar multiplication in matrices?

    -The distributive property in scalar multiplication relates to the fact that the scalar must be multiplied by each individual entry in the matrix, distributing the scalar across all elements.

Outlines
00:00
📈 Scalar Multiplication in Matrices

This paragraph introduces the concept of scalar multiplication in the context of matrices. It explains that scalar multiplication involves multiplying each individual entry of a matrix by a real number, known as the scalar. The process is akin to the distributive property, where the scalar is distributed across all elements. An example is provided to illustrate how multiplying a matrix by a scalar changes each entry accordingly. The paragraph sets the stage for further exploration of matrix multiplication, highlighting the importance of understanding the basic operations with matrices.

05:02
🔍 Matrix Multiplication: Requirements and Process

The second paragraph delves into the process of multiplying two matrices together. It emphasizes the necessity of matching the number of columns in the first matrix with the number of rows in the second matrix for the multiplication to be valid. The paragraph provides a detailed walkthrough of the row-by-column multiplication method, using a step-by-step example to demonstrate how to perform the operation. It also touches on the resulting order of the new matrix after multiplication, showing how the outer dimensions determine its size. The explanation is clear and methodical, ensuring that viewers can follow along and understand the principles behind matrix multiplication.

Mindmap
Keywords
💡Matrix
A matrix is a rectangular array of numbers, symbols, or expressions, arranged in rows and columns. In the video, matrices are the central objects of study, with operations such as multiplication being performed on them to demonstrate how their elements interact. For instance, the video discusses multiplying a matrix by a scalar and multiplying two matrices together, both of which involve altering the elements within the matrix based on specific rules.
💡Scalar Multiplication
Scalar multiplication is the process of multiplying every element of a matrix by a single, non-matrix value, known as a scalar. This operation results in a new matrix of the same dimensions, with each element being the product of the original element and the scalar. In the video, the concept is illustrated by multiplying a matrix by a scalar K, showing how each entry (a, b, c, etc.) is multiplied by K to obtain a new matrix with entries (Ka, Kb, Kc, etc.).
💡Order of a Matrix
The order of a matrix is the size of the matrix, expressed as a pair of integers (m, n), where m is the number of rows and n is the number of columns. This concept is crucial for matrix multiplication, as it determines whether two matrices can be multiplied and what the resulting matrix's order will be. In the video, the order is used to check if matrix A (M by N) can be multiplied by matrix B (N by P), ensuring the middle dimensions match.
💡Row by Column Multiplication
Row by column multiplication is the method used to multiply two matrices. It involves taking the dot product of each row of the first matrix with each column of the second matrix, resulting in a new matrix. The video explains this process step by step, showing how to calculate the elements of the resulting matrix by performing multiplications and additions between corresponding elements of rows and columns.
💡Distributive Property
The distributive property is a fundamental arithmetic rule stating that the product of a number and the sum of two other numbers is equal to the sum of the products of the number and each addend. In the context of the video, the distributive property is used to describe how a scalar is multiplied by each entry in a matrix during scalar multiplication. This property ensures that every element of the matrix is affected equally by the scalar.
💡Dot Product
The dot product is an operation that takes two equal-length sequences of numbers (usually coordinate vectors) and returns a single number. In the context of matrix multiplication, the dot product is used to calculate the entries of the resulting matrix by multiplying elements of one row with the corresponding elements of another column and summing the products. The video demonstrates this through the step-by-step process of multiplying two matrices together.
💡Matrix Multiplication
Matrix multiplication is an operation that combines two matrices into a third matrix, following specific rules. It is distinct from scalar multiplication and requires the number of columns in the first matrix to match the number of rows in the second matrix. The video provides a detailed explanation of how to perform matrix multiplication, including checking the order of the matrices and using row by column multiplication to calculate the resulting matrix's entries.
💡Matrix Elements
Matrix elements refer to the individual numbers or values that make up the entries of a matrix. These elements are arranged in a grid of rows and columns and are the basic components that undergo operations such as addition, subtraction, scalar multiplication, and matrix multiplication. The video discusses how these elements interact with each other and with scalar values during multiplication operations.
💡Non-Commutative Operation
A non-commutative operation is one that does not satisfy the commutative property, meaning that changing the order of the operands can result in a different outcome. In the context of matrix multiplication, this property is important because it means that the order in which matrices are multiplied matters; matrix A multiplied by matrix B is not necessarily the same as matrix B multiplied by matrix A. The video illustrates this by showing that flipping the order of the matrices prevents multiplication.
💡Resulting Matrix
The resulting matrix, also known as the product matrix, is the output matrix obtained from the multiplication of two matrices or from the scalar multiplication of a matrix. The size and elements of this matrix are determined by the specific rules of matrix multiplication, including the order of the matrices and the distributive and associative properties of multiplication. The video explains how the resulting matrix's order is derived from the orders of the matrices being multiplied and how its elements are calculated through row by column multiplication.
💡Matrix Dimensions
Matrix dimensions refer to the size of a matrix, which is defined by the number of rows and columns it contains. These dimensions are critical for matrix operations, particularly multiplication, as they determine the compatibility of matrices for multiplication and the size of the resulting matrix. The video emphasizes the importance of matching the number of columns in the first matrix with the number of rows in the second matrix for multiplication to be possible.
Highlights

The introduction of matrix multiplication concepts, including scalar and row by column multiplication.

Explanation of scalar multiplication, where a real number (scalar) is multiplied by each entry in a matrix.

Illustration of scalar multiplication with a 2x3 matrix and a scalar value of 3.

Discussion on the requirements for matrix multiplication, emphasizing the need for compatible matrix orders.

Clarification that the number of columns in the first matrix must match the number of rows in the second matrix for multiplication to be possible.

Demonstration of row by column multiplication using a 2x3 matrix and a 3x2 matrix as an example.

Step-by-step calculation of the product matrix through row by column multiplication.

Explanation of how the order of matrices dictates the possibility of multiplication and the order of the resulting matrix.

Another example provided, this time with matrices of orders 2x2 and 2x3, showing the process of multiplication.

Detail on how the outer numbers of the matrices determine the order of the resulting matrix after multiplication.

Row by column multiplication demonstrated with the provided example, showing the calculation of each entry in the resulting matrix.

Highlighting the difference in the resulting matrix's order when the order of the matrices is switched in multiplication.

Explanation that swapping the order of matrices for multiplication is not always possible, as demonstrated with the given matrix orders.

Conclusion of the video, summarizing the key points on matrix multiplication and its requirements.

Transcripts

Browse More Related Video

How To Multiply Matrices - Quick & Easy!

how to multiply 2x2 matrices

Multiplying Matrices

Defined and undefined matrix operations | Matrices | Precalculus | Khan Academy

Dimensions of identity matrix | Matrices | Precalculus | Khan Academy

Ch. 10.4 The Algebra of Matrices

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Matrix MultiplicationScalar MultiplicationRow-Column MethodLinear AlgebraMath TutorialEducational ContentMathematical ConceptsVideo ExplanationAlgebra TechniquesMathematics Learning