AP PHYSICS 1: Unit 5 FRQ 1 (AP Classroom)

Heinrich Physics

10 Apr 202026:04

EducationalLearning

32 Likes 10 Comments

TLDRIn this educational video, Mr. Heinrich discusses the principles of momentum and energy conservation in the context of a physics problem involving a block sliding down a ramp and colliding with another block. He explains the difference between elastic and inelastic collisions, and how the loss of mechanical energy as thermal energy during inelastic collisions affects the outcome. The video also outlines an experimental procedure for students to determine the relationship between the release height of a block and the resulting speed after a collision.

Takeaways

📚 The class is discussing AP Physics 1, focusing on Unit 5 which deals with momentum.
📌 The scenario involves a block released from a height (Block X) and another block (Block Y) it collides with.
🎯 The key physics principles for this Free Response Question (FRQ) are the conservation of energy and conservation of momentum.
🚫 Since there are no external non-conservative forces, the system is ideal for analyzing these conservation laws.
🔄 The collision between Block X and Block Y is perfectly inelastic, meaning they stick together after the collision.
🧠 Students are asked to derive an equation that relates the initial release height (HX) of Block X to the speed (Vs) of the two-block system after collision.
📐 The derived equation is in terms of fundamental constants (MX, MY, G, and HX) and shows the relationship between HX and Vs.
🔧 An experimental procedure is designed to graphically determine the relationship between the release height of Block X and the speed of the two-block system after collision.
📈 The experiment involves measuring quantities such as height (HX), masses (MX and MY), and velocity (Vs) using appropriate equipment like a meter stick and motion sensor.
🔄 The procedure includes releasing Block X from different heights and measuring the corresponding velocities to plot the relationship.
🔎 In Part C, the collision between blocks with the same mass is analyzed, revealing that the actual outcomes do not match the predictions for an elastic collision.
⚠️ The discrepancy is due to the collision being inelastic, with mechanical energy being converted into other forms like thermal energy, not perfectly conserved.

Q & A

What is the main topic of the classroom lecture?
-The main topic of the classroom lecture is the concept of momentum in AP Physics 1, specifically focusing on the analysis of a collision between two blocks on a ramp.
What type of collision is being discussed in the lecture?
-The collision being discussed is a perfectly inelastic collision, where the two blocks stick together after the impact.
What are the fundamental principles that should be used to analyze the system?
-The fundamental principles that should be used to analyze the system are the conservation of energy and the conservation of momentum.
How does the force of gravity affect the blocks in the experiment?
-The force of gravity is the driving force that causes block X to move down the ramp and collide with block Y. It is a conservative force and plays a crucial role in the conservation of energy analysis.
What is the role of friction in this experiment?
-Friction is not considered a significant factor in this experiment as there are no external non-conservative forces acting on the blocks during the collision.
How can the relationship between the release height of block X and the speed of the two-block system after collision be determined?
-The relationship can be determined by setting up and solving equations based on the conservation of energy and conservation of momentum principles, resulting in an equation that relates the initial release height H_X to the combined velocity V_s of the two-block system.
What is the purpose of the experimental design portion of the lecture?
-The purpose of the experimental design portion is to outline a procedure that students can use to graphically determine the relationship between the release height of block X and the speed of the two-block system after collision.
What equipment is needed to measure the necessary quantities for the experiment?
-The equipment needed includes a meter stick to measure height, a scale to measure the masses of the blocks, and a motion sensor to measure the velocity of the two-block system.
How does the experiment account for the difference in mass between block X and block Y?
-The experiment takes into account the difference in mass by including it in the conservation of momentum equation, where the masses of both blocks (M_X and M_Y) are used to calculate the common velocity (V_s) after the collision.
What is the discrepancy observed in Part C of the lecture?
-In Part C, the predicted speeds of block C after the collision, assuming an elastic collision, do not agree with the actual speeds observed. This discrepancy indicates that the collision is not elastic but inelastic, with some mechanical energy being lost to other forms of energy such as thermal energy.
How does the loss of mechanical energy during an inelastic collision affect the outcome of the experiment?
-The loss of mechanical energy during an inelastic collision results in a reduction of the rebound velocity of block Z, which is observed to be less than the theoretical velocity in an elastic collision. This indicates that not all kinetic energy is conserved, and some energy is transformed into other forms like thermal energy, sound energy, and light energy.

Outlines

00:00

📚 Introduction to Momentum and Collision Analysis

This paragraph introduces the topic of momentum within the context of an AP Physics 1 class. The teacher, Mr. Heinrich, sets the scene for a problem involving a block (Block X) released from a height and colliding with another block (Block Y). The students are prompted to consider the appropriate physics principles for analyzing this type of problem, which includes the conservation of momentum and energy. The teacher emphasizes the importance of understanding the difference between kinematics and energy principles, and how to apply these concepts to problems involving curved surfaces and collisions. The paragraph concludes with a focus on the need to derive equations that relate the release height of Block X to the speed of the two-block system after collision.

05:02

🧠 Deriving Equations for Collision Analysis

In this paragraph, the teacher guides the students through the process of deriving equations that describe the relationship between the initial release height (HX) of Block X and the speed (Vs) of the two-block system after a collision. The discussion revolves around the conservation of energy and momentum principles, highlighting the absence of external non-conservative forces like friction. The teacher illustrates how to set up equations using these principles, and how to relate the concepts of potential and kinetic energy, as well as momentum before and after the collision. The goal is to arrive at an equation that expresses Vs in terms of fundamental constants and the release height HX.

10:02

🔬 Experimental Design for Collision Analysis

This paragraph focuses on the experimental design aspect of the collision analysis problem. The teacher outlines the steps for designing an experiment that will allow students to graphically determine the relationship between the release height of Block X and the speed of the two-block system after collision. The paragraph details the quantities to be measured, such as the height HX and the masses MX and MY, and the equipment needed for these measurements, including a meter stick and a scale. The teacher then describes the overall procedure, which involves measuring the masses, setting up a motion sensor, releasing Block X, recording the velocity Vs, and repeating the process for multiple heights to average the Vs measurements. The emphasis is on reducing error and obtaining accurate data to understand the relationship between height and velocity in the context of collisions.

15:08

🤔 Analyzing Results of an Elastic Collision Hypothesis

In this paragraph, the teacher discusses a hypothetical scenario where Blocks W and D, which have the same mass, collide and the students predict an elastic collision. An elastic collision is one where no kinetic energy is lost, and the total kinetic energy before the collision is equal to the total kinetic energy after the collision. However, the actual results deviate from the predictions, indicating that the collision is not elastic. The teacher explains that the discrepancy arises because the collision is inelastic, meaning that some mechanical energy is lost to other forms of energy, such as thermal energy, sound energy, and light energy. This loss of mechanical energy results in a reduction of the rebound velocity of Block D (previously referred to as Block Z), which does not rebound as expected in an elastic collision.

20:11

🙏 Conclusion and Encouragement for Future Learning

The final paragraph serves as a conclusion to the video lesson, reminding students to continue their studies as they progress through Unit 7 of their AP Physics curriculum. The teacher encourages students to stay engaged with the material and anticipates covering the entire unit to prepare them for the AP Physics exam. The paragraph ends on a positive note, with a reminder for students to subscribe for more helpful content.

Mindmap

Keywords

💡Momentum

Momentum is a physical quantity that represents the motion of an object and is defined as the product of an object's mass and velocity. In the video, momentum is a key concept used to analyze the collision between two blocks, where the law of conservation of momentum dictates that the total momentum before and after the collision remains constant. This principle is crucial in determining the behavior and velocities of the blocks after the collision.

💡Energy Conservation

Energy conservation is a fundamental principle in physics stating that the total amount of energy in an isolated system remains constant over time. In the context of the video, this concept is applied to analyze the system of blocks where potential energy is converted into kinetic energy as the block rolls down the ramp. The principle is also used to explain the difference between perfectly inelastic and elastic collisions, highlighting the transformation of mechanical energy into other forms like thermal energy during the collision process.

💡AP Physics

AP Physics refers to the Advanced Placement Physics course and examination offered by the College Board. The video's content is centered around the teaching and understanding of concepts relevant to this course, such as momentum and energy conservation, which are essential topics for students preparing for the AP Physics 1 exam. The video aims to provide insights and problem-solving strategies that align with the curriculum and objectives of the AP Physics course.

💡Collision

A collision in physics occurs when two or more objects interact with each other, transferring momentum and energy in the process. The video discusses different types of collisions, such as perfectly inelastic and elastic collisions, and uses the concept to explain the experimental setup and outcomes involving the collision of two blocks with different masses. Understanding collisions is crucial for grasping the dynamics of particle interactions and the conservation laws at play.

💡Kinematics

Kinematics is a branch of physics that deals with the motion of objects without considering the forces that cause the motion. In the video, kinematics is mentioned as a potential method for analyzing the motion of the blocks, but it is noted that it is less applicable in this scenario due to the curved surface and the presence of other forces like gravity. Kinematics is typically used to describe motion in terms of displacement, velocity, and acceleration without regard to the causes of motion.

💡Friction

Friction is a force that opposes the relative motion or tendency of such motion of two surfaces in contact. In the video, it is mentioned that friction is not a significant external force acting on the blocks during the experiment, which simplifies the analysis of the system. The absence of friction allows for a cleaner application of the conservation laws, as it is a non-conservative force that could otherwise complicate the energy and momentum calculations.

💡Inelastic Collision

An inelastic collision is a type of collision where kinetic energy is not conserved; some of the energy is transformed into other forms, such as heat or sound. In the video, this concept is explored through the experimental results, which show that the actual velocities of the blocks after the collision are less than predicted, indicating that kinetic energy has been converted into thermal energy and other forms, thus confirming the collision is inelastic.

💡Elastic Collision

An elastic collision is a type of collision where both momentum and kinetic energy are conserved. In the video, it is mentioned that the students initially theorize that the collision between two blocks of equal mass would be elastic, meaning that the total kinetic energy before the collision would be equal to the total kinetic energy after the collision. However, the results indicate that the collision is not elastic, as there is a discrepancy between the predicted and actual velocities of the blocks after the collision.

💡Thermal Energy

Thermal energy, also known as heat energy, is the internal energy of an object due to the random motion of its molecules. In the video, it is explained that during an inelastic collision, some of the mechanical energy is converted into thermal energy. This conversion occurs as the molecules of the colliding objects interact, increasing their kinetic energy at the microscopic level, which manifests as a rise in temperature or heat.

💡Velocity

Velocity is a vector quantity that describes the rate of change of an object's position with respect to time, and it has both magnitude (speed) and direction. In the video, velocity is a central concept used to describe the motion of the blocks before and after the collision. The analysis involves calculating the initial velocity of the first block as it rolls down the ramp and determining the common velocity of the two-block system after the collision, which is essential for understanding the dynamics of the system.

💡Experimental Procedure

An experimental procedure is a detailed step-by-step process used to conduct a scientific experiment. In the video, the teacher outlines an experimental procedure for determining the relationship between the release height of a block and the speed at which the two-block system travels after collision. This procedure involves measuring quantities such as height and mass, setting up equipment like a motion sensor, and conducting the experiment multiple times to obtain accurate results.

Highlights

The class is discussing AP Physics 1, focusing on Unit 5 about momentum.

The scenario involves a block released from a height, which will hit another block.

The fundamental physics principles for this Free Response Question (FRQ) are the conservation of energy and momentum.

In the absence of external non-conservative forces, the conservation laws are applicable.

The collision described is a perfectly inelastic collision, where the two blocks stick together.

The derivation of the equation relating the initial release height (HX) and the speed (VS) of the two-block system after collision is discussed.

An experimental procedure is designed to determine the relationship between the release height of block X and the speed of the two-block system after collision.

The procedure involves measuring the mass of the blocks with a scale and the height with a meter stick.

A motion sensor is used to measure the velocity of the two-block system.

The experiment is conducted by releasing block X from different heights and recording the velocities.

The results from blocks W and D's collision indicate an inelastic collision, not elastic as theorized.

The discrepancy in predicted and actual speeds is due to the loss of mechanical energy during the collision.

Mechanical energy is converted into other forms of energy, such as thermal energy, sound energy, and light energy.

The loss of mechanical energy results in a reduction of the rebound velocity of block Z.

The conservation of momentum is still valid even in inelastic collisions.

The experiment demonstrates the practical application of the conservation of energy and momentum principles.

The class discussion and experiment aim to prepare students for the AP Physics exam, covering material up to Unit 7.

Transcripts

Browse More Related Video

Elastic and Inelastic Collisions

Differentiating Between Elastic and Inelastic Collisions | Physics in Motion

Introduction to Elastic and Inelastic Collisions

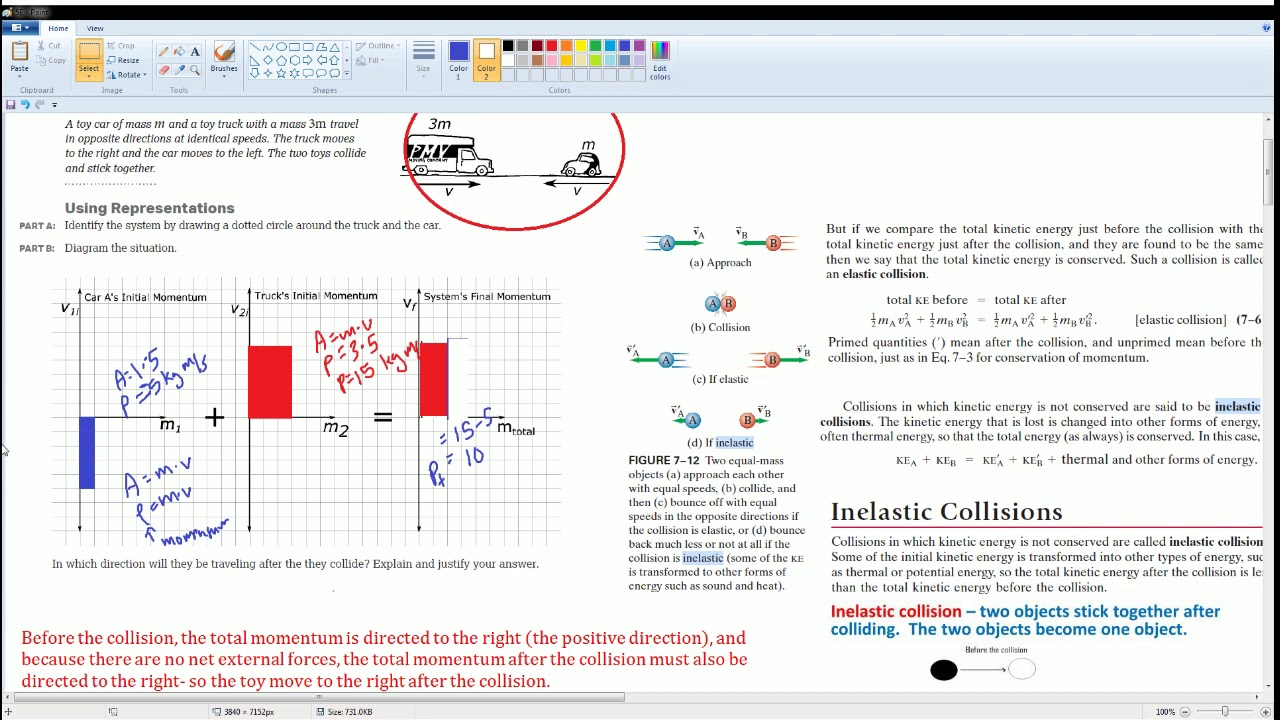
AP Physics Workbook 5.E Conservation of momentum in Inelastic Collisions

Conservation of Linear Momentum

AP PHYSICS 1: Unit 5 FRQ 2 (AP Physics Classroom)

Related Tags

Physics Concepts Momentum Analysis Energy Conservation AP Physics 1 Collision Experiment Mechanical Energy Inelastic Collision Educational Content Classroom Activity Science Education