What Math Classes Do Engineers (and Physics Majors) Take?
TLDRThis educational video delves into the fundamental math support classes that are essential across various engineering and science majors, including electrical, mechanical, aerospace, biomedical, civil, industrial, and computer engineering, as well as physics and chemistry. It provides a detailed overview of the calculus series—Calculus I, II, and III—explaining key concepts such as limits, derivatives, and integrals, and their profound importance in engineering and physics. The video further explores techniques of integration, series and sequences, Taylor and Maclaurin series, multivariable calculus, and basics of differential equations and linear algebra. Emphasizing the applicability of these mathematical tools in solving complex real-world problems, the video aims to prepare students for their rigorous academic journey in engineering and science disciplines.
Takeaways
- 📚 Undergraduate engineers, regardless of their specialization, share a common foundation in math support classes, including calculus, series, and linear algebra.
- 🌟 Calculus is pivotal across all engineering disciplines, emphasizing concepts like limits, derivatives, and integrals which are crucial for understanding physical systems.
- 📊 Derivatives play a key role in physics, as they help in analyzing velocities and system dynamics, represented by the slope of a curve at a particular point.
- 🔄 Integrals are used to calculate areas under curves, which can represent the change in position when velocity is plotted against time.
- 📈 Advanced calculus topics like integration techniques, series and sequences, Taylor and Maclaurin series are covered in depth, preparing students for more complex problem-solving.
- 📱 Multivariable calculus, including partial derivatives and triple integrals, is essential for understanding three-dimensional systems and is applicable in fields like physics and electromagnetism.
- 🔍 Engineering students learn to apply calculus in solving real-world problems, such as those involving electromagnetic waves, which are foundational in electrical engineering.
- 🧠 The importance of linear algebra is highlighted by its role in matrix operations, which is fundamental to engineering software like MATLAB.
- 🔢 Differential equations are a key subject for engineers, as they model complex motions and systems, with broad applications across various engineering fields.
- 🎓 Physics majors will encounter calculus more frequently than other disciplines, while computer and software engineers may focus less on high-level math.
- 💡 The video script underscores the universal nature of mathematical principles in engineering education and their application to diverse engineering problems.
Q & A
What common math support classes do most engineers have to take regardless of their specific engineering major?
-Most engineers, regardless of their major, have to take nearly identical math support classes, which include calculus, series calculus one, two, and three, and other foundational math courses.
What is the significance of learning calculus in an engineering curriculum?
-Calculus is significant in an engineering curriculum because it forms the foundation for analyzing systems with changing variables, such as velocities in physics, and is used extensively in various engineering and physics equations.
How does the concept of a derivative in calculus relate to real-world physical phenomena?
-The concept of a derivative relates to real-world physical phenomena by representing the rate of change at a specific point. For example, the slope of a position-time graph represents velocity, and the instantaneous slope at a particular moment gives the instantaneous velocity of an object.
What is the purpose of learning integrals in calculus?
-Integrals are used to calculate the accumulated change over a period, such as the area under a velocity curve representing the change in position. They are essential for solving problems where you need to find the sum of an infinite series of infinitesimally small quantities.
What are the main topics covered in Calculus 2 for engineering students?
-Calculus 2 for engineering students covers various integration techniques, including u-substitution and other methods for integrating functions that don't allow for simple u-substitution. It also covers series and sequences, including convergence and divergence tests.
How do Taylor and Maclaurin series simplify complex functions?
-Taylor and Maclaurin series simplify complex functions by approximating them with polynomials. This allows for easier computation and manipulation of functions, especially when dealing with small values of the variable, as seen in the approximation of e^x with its Maclaurin series.
What is multivariable calculus, and how does it differ from single-variable calculus?
-Multivariable calculus extends the concepts of single-variable calculus to functions with more than one variable. It introduces partial derivatives, double and triple integrals, and vector analysis, which are essential for solving problems involving three-dimensional spaces and multiple variables.
Why is vector analysis important in physics and engineering?
-Vector analysis is important in physics and engineering because it helps in determining work done on objects moved through a vector field, such as forces in a whirlpool. It is also crucial in electromagnetism for understanding the behavior of electromagnetic waves like radio, microwaves, and visible light.
What is the role of differential equations in engineering?
-Differential equations play a crucial role in engineering as they represent and solve complex motions and systems, such as a mass on a spring subject to friction. They are used across various engineering disciplines to model real-world problems.
How does linear algebra connect to matrix algebra and its applications?
-Linear algebra connects to matrix algebra by providing the foundation for solving systems of equations using matrices. It is essential for understanding and applying matrix operations, which are fundamental in engineering software like MATLAB and are used for tasks such as graphing functions.
Why is MATLAB important for engineering students?
-MATLAB is important for engineering students because it is a powerful tool for matrix math, which is at the core of many engineering calculations. It can graph functions, solve complex equations, and is widely used in various engineering disciplines for its computational capabilities.
Outlines
📚 Introduction to Engineering and Math Fundamentals
This paragraph introduces the common math support classes that engineers from various disciplines, including physics and chemistry majors, have to take during their undergraduate studies. It emphasizes the universality of these classes across different engineering fields. The video aims to provide a detailed understanding of these foundational courses, starting with calculus. The explanation begins with calculus basics such as limits, derivatives, and integrals, highlighting their importance in physics and engineering. The concept of derivatives is linked to real-world applications like calculating velocities and analyzing systems with changing velocities. Integrals are introduced as a method to find the area under a curve, which is crucial for understanding changes in position over time. The paragraph sets the stage for a deeper dive into the specifics of engineering math classes.
📈 Advanced Calculus Techniques and Series
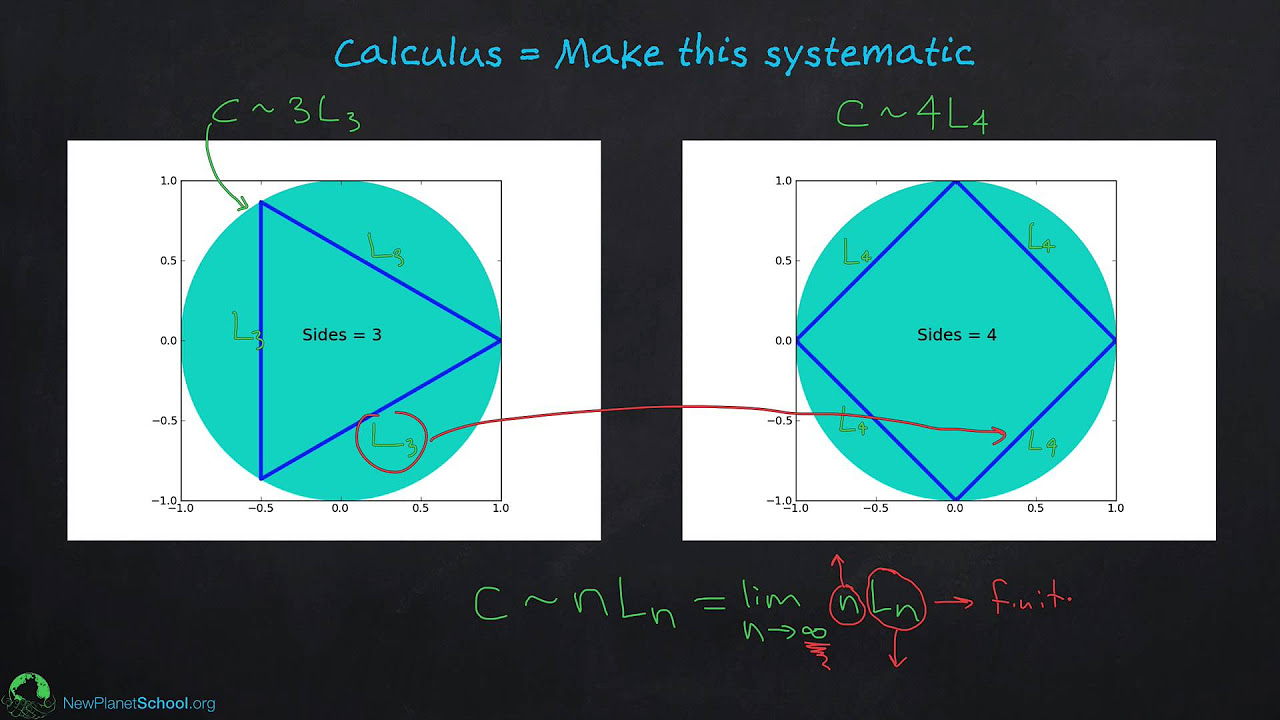
The second paragraph delves into the specifics of calculus courses that engineers encounter, such as Calculus 2 and Calculus 3. It discusses the various integration techniques learned in Calculus 2, which are essential but often lack direct real-world applications. The paragraph also covers the concept of series and sequences, focusing on determining convergence or divergence. The Taylor and Maclaurin series are introduced as tools for approximating functions, with examples from physics to illustrate their practical applications. The paragraph concludes with an overview of multivariable calculus, emphasizing the transition from two-dimensional to three-dimensional problem-solving and the introduction of partial derivatives and multiple integrals.
🌐 Applications of Calculus in Physics and Engineering
This paragraph discusses the application of calculus in physics and engineering, particularly in understanding the behavior of systems over time. It covers the final calculus class, which includes vector analysis and its relevance to electromagnetism and the study of forces in a vector field. The importance of understanding work done on objects in physics and the role of vector fields in electromagnetic wave propagation is highlighted. The paragraph also touches on the basics of differential equations, which are crucial for modeling complex motions. The connection between matrix algebra and the use of MATLAB in engineering is established, emphasizing the significance of these mathematical tools in solving real-world engineering problems. The summary underscores the universality of these mathematical concepts across engineering disciplines and their importance beyond the classroom.
Mindmap
Keywords
💡Calculus
💡Derivatives
💡Integrals
💡Series and Sequences
💡Multivariable Calculus
💡Vector Analysis
💡Differential Equations
💡Linear Algebra
💡MATLAB
💡Physics
💡Engineering Majors
Highlights
Undergraduate engineering curriculum typically requires similar math support classes across different majors.
Engineers and physics majors must take calculus, series calculus one, two, and three, regardless of their specific major.
Calculus one covers limits, derivatives, and integrals, foundational to understanding physical systems with changing velocities.
Derivatives are crucial in engineering and physics as they represent the instantaneous slope or velocity at a point.
Integrals are used to calculate the area under a curve, which in physics can represent the change in position.
Calculus 2 introduces various integration techniques and the concept of series and sequences.
The Taylor and Maclaurin series are used to approximate functions with polynomials, simplifying complex equations in physics.
Calculus 3, or multivariable calculus, involves learning to graph in three dimensions and understanding partial derivatives.
Double and triple integrals in calculus 3 are used to calculate the volume under three-dimensional curves.
Vector analysis in the last calculus class is essential for understanding work done in physics and is applicable to electromagnetism.
Differential equations are a required class for engineers, teaching how to solve complex motion equations.
Linear algebra is an important part of the engineering curriculum, foundational for matrix operations and essential for using MATLAB.
MATLAB, short for matrix lab, is a widely used program in engineering that fundamentally relies on matrix math.
Engineering majors will encounter calculus and other math classes as essential tools for solving real-world problems.
The difficulty of calculus in engineering classes is often less about the math itself and more about applying it to practical engineering solutions.
Transcripts
Browse More Related Video

What Math Classes Do Physics Majors Take?

How to Take All the Math Classes You Need Right From Your Computer

A Look at Some Higher Level Math Classes | Getting a Math Minor
Calculus: What Is It?

LIMITS CALCULATOR TECHNIQUES - DIFFERENTIAL CALCULUS | ENGINEERING BOARD EXAM REVIEW | YU JEI ABAT

Dear Calculus 2 Students, This is why you're learning Taylor Series
5.0 / 5 (0 votes)
Thanks for rating: