Why are the formulas for the sphere so weird? (major upgrade of Archimedes' greatest discoveries)
TLDRThis Mathologer video celebrates its 100th episode with a groundbreaking exploration of the sphere's volume and surface area. Collaborating with mathematician and 3D printing artist Henry Segerman, the video introduces a novel method to visualize the derivation of the sphere's volume formula using a baggage carousel analogy and a hemisphere-to-cylinder transformation. It also presents a unique unfolding technique to demonstrate the sphere's surface area as four times the area of its shadow circle, highlighting the historical context of these discoveries and their significance in mathematical history.
Takeaways
- 🎉 The video marks the 100th Mathologer episode and the first collaboration with mathematician and 3D printing artist Henry Segerman.
- 🌐 The video introduces a new, game-changing method for understanding the volume of a sphere using a conveyor belt analogy and geometric transformations.
- 🔄 The process of turning a hemisphere inside out results in a shape that is approximately a cylinder with a cone carved out from the top, leading to a new way to derive the volume of a sphere.
- 📐 The volume of a sphere is shown to be 4/3 times pi times the radius cubed (V = 4/3 * π * r^3), by subtracting the volume of a cone from a cylinder and doubling it.
- 🔺 The concept of using the circle and ring cross-sections to prove that the inside-out shape is a cylinder minus a cone is explored, leveraging the idea that equal areas at all heights imply equal volumes.
- 📚 The video connects the new method back to historical mathematical discoveries by Archimedes and Bonaventura Cavalieri, highlighting the evolution of mathematical thought.
- 🚀 The video presents an innovative insight where replacing the hemisphere with a paraboloid in the conveyor belt analogy leads to a new understanding of the volume of a paraboloid.
- 🌍 The surface area of a sphere is derived using a 3D 'onion proof', showing that the volume of a sphere is one-third the base area times the height, which simplifies to one-fourth the surface area times the radius.
- 🎨 The video showcases a creative 'unfolding' of the sphere into a circle of double the radius, providing a visual and intuitive understanding of why the surface area formula is 4 times pi times the radius squared (A = 4 * π * r^2).
- 🤓 A calculus-based explanation is given for the relationship between the volume and surface area formulas of a sphere, highlighting that the surface area formula is the derivative of the volume formula.
- 🌟 The video emphasizes the beauty and elegance of mathematical proofs, and how they can reveal deep insights into the nature of geometric shapes and their properties.
Q & A
What is the significance of the 100th Mathologer video?
-The 100th Mathologer video is significant because it marks a milestone in the series, and it features a special collaboration with mathematician and 3D printing artist Henry Segerman. It also introduces game-changing discoveries about the sphere, making it a mathematical premier.
How does the baggage carousel trick help in understanding the volume of a sphere?
-The baggage carousel trick visually demonstrates the process of turning a hemisphere inside out into a shape that is approximately a cylinder with a cone carved out from the top. This trick allows for the derivation of the sphere's volume formula by subtracting the volume of the cone from the volume of the cylinder and then doubling it, leading to the formula 4/3πr^3.
What is the relationship between the volume of a hemisphere and the volume of a cylinder and cone?
-The volume of a hemisphere is equal to the volume of a cylinder minus the volume of a cone with the same radius and height. This relationship is used to derive the volume formula of a sphere, which is 4/3πr^3 for the hemisphere and doubled for the entire sphere.
How did Bonaventura Cavalieri contribute to the understanding of the sphere's volume?
-Bonaventura Cavalieri contributed to the understanding of the sphere's volume by being the first to realize that the cylinder-minus-cone configuration could be used to derive the volume formula of the sphere. He used a method that involved showing that the circle and ring cross-sections of the two shapes have the same area at all heights and applied Cavalieri's principle to conclude that the two shapes must have the same volume.
What is the volume formula of a paraboloid, and how is it related to the cylinder?
-The volume of a paraboloid is equal to half the volume of the surrounding cylinder. This relationship is derived from the process of turning a hemisphere into a cylinder-minus-cone shape and replacing the hemisphere with a paraboloid, resulting in the inside-out shape being the surrounding cylinder minus the same paraboloid.
What is the surface area formula of a sphere, and how is it related to the area of a circle?
-The surface area formula of a sphere is 4πr^2, which is exactly 4 times the area of a circle with the same radius (πr^2). This relationship can be visually understood by unfolding the sphere's surface into a larger circle of twice the radius, where each point on the sphere corresponds to a point on the circle with the same area.
How does the concept of an onion proof help in understanding the area formula for a circle?
-The onion proof helps in understanding the area formula for a circle by visualizing a circle as being made up of infinitely many concentric circles. By cutting and straightening these circles, the disk unfolds into a triangle with a height equal to the radius and a base equal to the circumference. The area of the circle is then derived as half the product of its circumference and height, without involving π directly.
What is the connection between the derivative of the volume formula and the surface area formula of a sphere?
-The surface area formula of a sphere (4πr^2) is the derivative of the volume formula (4/3πr^3). This means that by taking the derivative of the volume function with respect to the radius, we obtain the surface area function, demonstrating a direct mathematical relationship between the two properties of a sphere.
How does Andrew's area-preserving transformation of the sphere into a circle help in understanding the surface area formula?
-Andrew's area-preserving transformation demonstrates that the surface area of the sphere is equal to the area of the circle with twice the radius. This transformation is visual and intuitive, showing that any region on the sphere will have the same area when transformed onto the larger circle, thus providing a clear understanding of why the surface area formula is 4πr^2.
What is the significance of Archimedes' claw contraption in the video?
-Archimedes' claw contraption is a 3D printed model that visually demonstrates the area-preserving transformation of the sphere's surface into a circle. It helps to illustrate the concept that the surface area of the sphere is exactly 4 times the area of its shadow circle, providing a tangible and interactive way to understand the mathematical principles discussed in the video.
How does the video connect the concepts of volume and surface area of a sphere to the historical work of mathematicians like Archimedes and Cavalieri?
-The video connects the concepts of volume and surface area of a sphere to the historical work of mathematicians like Archimedes and Cavalieri by discussing their original methods and proofs for deriving these formulas. It highlights the evolution of mathematical thought and how modern insights, like those of Andrew and Henry Segerman, build upon and enhance the work of these historical figures.
Outlines
🎉 Celebrating a Milestone and Mathematical Innovations
This paragraph marks the beginning of a special Mathologer video, the 100th episode, and introduces a first-time collaboration with mathematician and 3D printing artist Henry Segerman. The celebratory tone is combined with an exciting preview of groundbreaking mathematical discoveries about spheres that will be unveiled in the video. The analogy of a baggage carousel demonstrates a novel approach to understanding the volume of a sphere, setting the stage for an exploration of mathematical history and innovative ideas.
🔍 Verifying the Inside-Out Hemisphere Transformation
The paragraph delves into the mathematical validation of the inside-out hemisphere transformation, ensuring that the resulting shape is indeed a cylinder minus a cone. The detailed examination involves visualizing the process and proving the linear relationship between the shapes. The discussion also touches on the historical context, mentioning Bonaventura Cavalieri and his role in the development of the volume formula for a sphere, as well as the influence of Archimedes' work on subsequent mathematicians.
🌟 Upgrading Ancient Mathematical Discoveries
This section highlights the significance of the new method for deriving the volume of a sphere, positioning it as an upgrade to Cavalieri's and Archimedes' original proofs. The video script suggests that this new approach is a part of the ongoing mathematical legacy, contributing to the historical development of the field. Additionally, the paragraph introduces a fascinating insight related to replacing the hemisphere with a paraboloid and challenges the viewer to work out the details, further emphasizing the educational and interactive nature of the content.
🍄 The洋葱 Proof and 3D Extensions
The paragraph discusses the '洋葱' or 'onion proof', a method for understanding the relationship between the area and circumference of a circle without involving pi. The concept is extended into three dimensions, using the idea of a layered ball to derive the volume formula for a sphere. The video script playfully uses the onion analogy and dad jokes to make complex mathematical ideas more accessible and engaging for the audience.
📈 Deriving Surface Area Formulas and the Power of Calculus
The focus of this paragraph is on deriving the surface area formula for a sphere, both through a simple argument connected to the volume formula and through calculus, by recognizing the surface area formula as the derivative of the volume formula. The video script also touches on the historical significance of these formulas and their aesthetic appeal, highlighting the elegance and simplicity of mathematical proofs.
🌍 Unfolding the Sphere and Area-Preserving Transformations
The paragraph presents a novel way of understanding why the surface area formula for a sphere is what it is, using an ingenious area-preserving transformation of the sphere's surface into a larger circle. The explanation involves the concept of meridians and the unfolding of the sphere, providing a visual and intuitive understanding of the relationship between the sphere and its shadow circle. The video script also discusses the potential for a more rigorous mathematical proof to support this transformation.
🎨 The Magic of 3D Moons and Archimedes' Claw
This section delves into the specifics of 3D moon shapes and their role in transforming the surface of a sphere into a circle without distorting areas. The video script introduces Henry's爪 contraption, a 3D printed version of Archimedes' claw, and explores the implications of this invention. The explanation involves a detailed look at the 3D moons, their unfolding, and the area-preserving properties of the transformation, ultimately reinforcing the validity of the sphere-to-circle area equivalence.
Mindmap
Keywords
💡Mathologer
💡Sphere
💡Volume
💡Surface Area
💡Archimedes
💡Cylinder
💡Cone
💡Baggage Carousel
💡3D Printing
💡Archimedes' Claw
💡Onion Proof
Highlights
The 100th Mathologer video marks a special milestone with unique content and collaborations.
A collaboration with mathematician and 3D printing artist Henry Segerman introduces a new perspective on mathematical concepts.
The video presents a new, game-changing discovery about the sphere, offering insights known only to a few mathematicians.
A creative demonstration using a baggage carousel analogy explains the concept of turning a circle inside out.
The inside-out transformation of a circle leads to the discovery that a hemisphere can be represented as a cylinder minus a cone.
The volume of a sphere is derived in a novel way by subtracting the volume of a cone from a cylinder and then doubling the result.
The concept of volume is explored through the innovative use of circular conveyor belts and figure 8 dances.
The video delves into the history of mathematics, mentioning the achievements of Archimedes and Bonaventura Cavalieri in the context of the sphere's volume.
A new method for understanding the volume of a sphere is introduced, building upon and upgrading the discoveries of Cavalieri and Archimedes.
The video presents a challenge to the viewers to explore the volume of a paraboloid using the inside-out transformation concept.
The surface area of a sphere is explored through a simple and beautiful argument involving the concept of an onion proof.
The video demonstrates that the surface area formula of a sphere is the derivative of its volume formula, showcasing the beauty of calculus.
The surface area of a sphere is shown to be four times the area of its shadow circle, providing an intuitive understanding of the formula.
An innovative unfolding of the sphere's surface into a larger circle introduces a new way of understanding the area formula.
The video introduces Andrew's ingenious area-preserving transformation, which has a magical property of not distorting area.
The concept of area preservation is visually demonstrated using a 3D printed version of Archimedes' claw, a collaboration with Henry Segerman.
The video provides a rigorous mathematical check to ensure the validity of the inside-out shape transformation and the derived formulas.
The video concludes with a call to explore more about Archimedes' claw and its implications in a potential part 2, hinting at the depth of mathematical concepts yet to be discovered.
Transcripts
Browse More Related Video
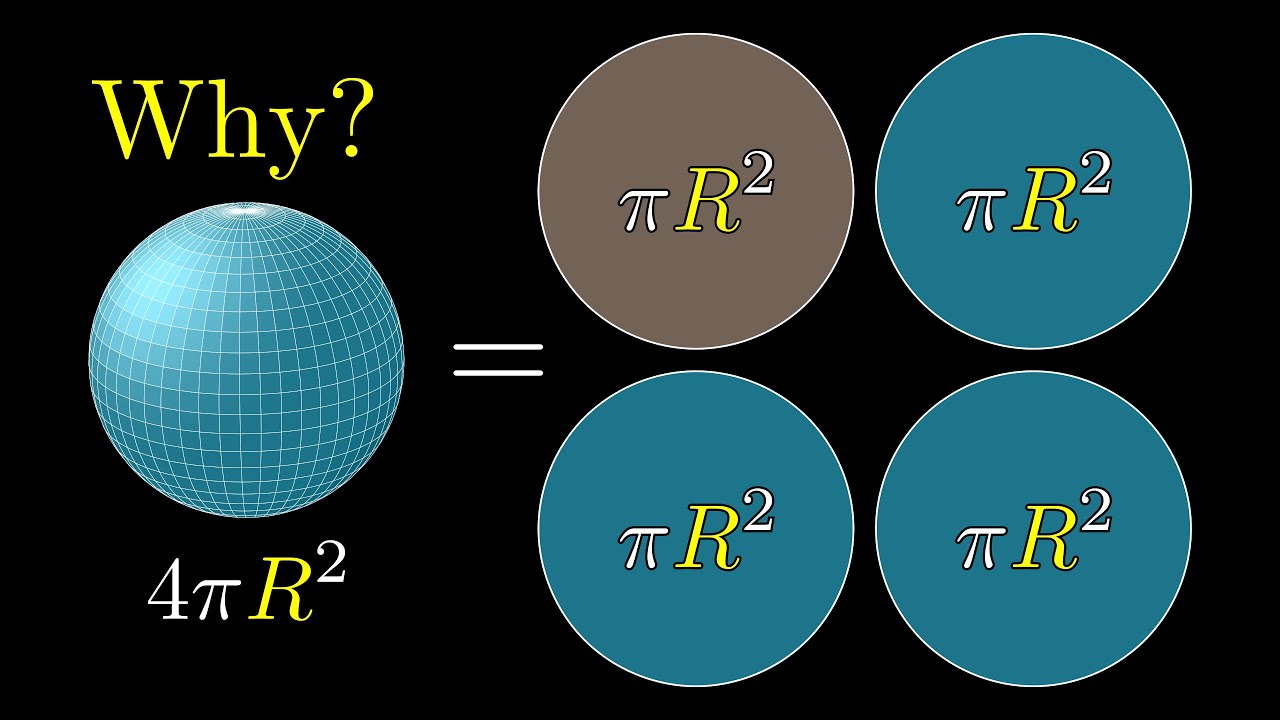
But why is a sphere's surface area four times its shadow?

Understanding the Volume of a Sphere Formula [Using High School Geometry]

Physics 37.1 Gauss's Law Understood (3 of 29) What is Gauss' Law?

Optimization Cylinder Problem

Maximum Surface Area | MIT 18.01SC Single Variable Calculus, Fall 2010

Optimisation Grade 12: Maximum Volume Cylinder
5.0 / 5 (0 votes)
Thanks for rating: