(Part 2 of 2) An Introductory Projectile Motion Problem with an Initial Horizontal Velocity

Flipping Physics
23 Apr 201407:57
EducationalLearning
32 Likes 10 Comments

TLDRIn the video, Mr. P and his students explore projectile motion, focusing on determining the final velocity of a ball before it lands in a bucket. They use the UAM equation to calculate the ball's velocity in the y direction and apply the Pythagorean theorem to find the resultant velocity. The discussion also covers the importance of considering both the magnitude and direction of velocity, leading to the conclusion that the ball has a velocity of 5.8 meters per second at an angle of approximately 50.3 degrees in front of the negative y axis. The lesson emphasizes understanding separate x and y motion components in projectile problems.

Takeaways
  • ๐Ÿ“Œ The problem discussed is a projectile motion scenario with an object having an initial horizontal velocity.
  • ๐Ÿ”„ The final velocity of the ball is determined using the UAM (Velocity, Acceleration, and Displacement) equation focusing on the y direction.
  • ๐Ÿงฎ The initial velocity in the y direction is zero, and the acceleration is the constant gravitational value of -9.81 m/sยฒ.
  • ๐Ÿ“ˆ The final velocity in the y direction is calculated to be 3.7 m/s (with two significant figures) downward due to the negative displacement.
  • ๐Ÿ”บ The final velocity we are solving for is the resultant vector, which is the hypotenuse of the triangle formed by the x and y components of velocity.
  • ๐ŸŒŸ The ball travels at a constant velocity in the x direction at 4.4694444 m/s, which remains unchanged throughout the motion.
  • ๐Ÿ”ข The magnitude of the final velocity is found using the Pythagorean theorem, which results in 5.80602 m/s (rounded to 5.8 m/s with two significant figures).
  • ๐ŸŽฏ The direction of the final velocity is determined by calculating the angle theta, which is approximately 50.3 degrees in front of the negative y axis.
  • ๐Ÿš— The hand remains directly above the ball because both the car and the ball move at the same constant horizontal velocity.
  • ๐ŸŒ๏ธโ€โ™‚๏ธ The ball appears to move straight down from the perspective of the hand due to the constant horizontal velocity and the acceleration acting only in the y direction.
  • ๐Ÿ›ค๏ธ Despite the same horizontal displacement, the ball travels farther than the hand because it follows a parabolic path due to the combined x and y motion, whereas the hand only moves linearly in the x direction.
Q & A

  • What type of motion problem is being discussed in the transcript?

    -The problem discussed is a projectile motion problem involving an object with an initial horizontal velocity.

  • What was the main objective of the problem?

    -The main objective was to determine the final velocity of the ball right before it lands in the bucket.

  • Which equation did Billy initially attempt to use to find the final velocity?

    -Billy initially attempted to use the UAM equation (velocity final squared equals velocity initial squared plus two times acceleration times change in position).

  • What was the direction of the ball's initial velocity?

    -The ball's initial velocity was entirely horizontal.

  • What was the acceleration in the y direction, and what was its effect on the final velocity?

    -The acceleration in the y direction was negative 9.81 m/s^2, which, when combined with the displacement in the y direction, resulted in a final velocity of 3.7 m/s downwards.

  • How did the group determine the final velocity in the x direction?

    -The final velocity in the x direction was the same as the initial and middle velocities since the ball was moving at a constant horizontal velocity of 4.4694444 m/s.

  • What trigonometric method was used to find the magnitude of the final velocity?

    -The Pythagorean theorem (a squared plus b squared equals c squared) was used to find the magnitude of the final velocity.

  • What was the calculated magnitude of the final velocity?

    -The calculated magnitude of the final velocity was 5.80602 m/s, which was rounded to 5.8 m/s with two significant figures.

  • How was the direction of the final velocity determined?

    -The direction of the final velocity was determined by calculating the angle theta using the inverse sine of the ratio of the final velocity in the x direction to the total final velocity.

  • What was the angle of the final velocity relative to the negative y axis?

    -The angle of the final velocity was approximately 50.3 degrees in front of the negative y axis.

  • Why did Mr. P's hand always remain directly above the ball?

    -Mr. P's hand remained directly above the ball because the car, his hand, and the ball all moved at the same constant horizontal velocity, resulting in the same displacement in the x direction.

  • How does the displacement of the ball differ from that of Mr. P's hand?

    -While the ball moves in both x and y directions (resulting in a parabolic path), Mr. P's hand only moves in the x direction (a straight line). Thus, even though their x displacements are the same, the ball travels farther due to its additional y displacement.

Outlines
00:00
๐Ÿ“š Projectile Motion Analysis

This paragraph introduces the problem of projectile motion, focusing on determining the final velocity of a ball before it lands in a bucket. The discussion involves the use of the UAM equation to calculate the final velocity in the y-direction, considering the initial horizontal velocity and the acceleration due to gravity. The groupไบ’ๅŠจไฝœ through the problem, with Billy leading the calculations and Bobby providing insights on the importance of considering the direction of the velocity. The final velocity in the y-direction is determined to be 3.7 meters per second downward. Bo raises a valid point about the need to consider the x-direction velocity as well, which is constant at 4.4694444 meters per second. The paragraph concludes with an explanation of resultant vectors and the need to find the magnitude and direction of the final velocity.

05:02
๐Ÿ“ Calculating Final Velocity Vector

In this paragraph, the group continues their analysis of the projectile motion problem, focusing on calculating the final velocity vector by considering both the x and y components. Bobby uses the Pythagorean theorem to find the magnitude of the final velocity, which is approximately 5.8 meters per second. The group debates the sign (positive or negative) of the final velocity, with Billy arguing for a positive value since the ball is moving to the right, and Bo for a negative value as the ball is moving downward. Bobby clarifies that they have only calculated the magnitude and that the direction needs to be determined. Mr. P then calculates the angle theta, finding that the final velocity is at an angle of 50.3354 degrees in front of the negative y-axis. The paragraph ends with a discussion on the importance of understanding the separate motions in the x and y directions and the practical application of this knowledge in the real-world scenario of the ball falling into the bucket.

Mindmap
Keywords
๐Ÿ’กProjectile Motion
Projectile motion refers to the movement of an object that is launched into the air and is influenced only by gravity. In the video, this concept is central as it describes the path of the ball being dropped and its motion through the air before landing in the bucket. The problem-solving process involves analyzing the separate components of motion in the horizontal (x) and vertical (y) directions, which are essential for understanding the final velocity of the ball.
๐Ÿ’กInitial Velocity
Initial velocity is the speed at which an object starts moving. In the context of the video, the ball has an initial velocity that is entirely horizontal. This is a critical piece of information for the physics problem as it sets the stage for the subsequent calculations of the ball's motion through the air.
๐Ÿ’กAcceleration
Acceleration is the rate at which an object's velocity changes over time. In the video, the only acceleration acting on the ball is the acceleration due to gravity, which is consistently downward and has a value of approximately 9.81 meters per second squared. This acceleration affects the ball's velocity in the vertical direction as it falls towards the bucket.
๐Ÿ’กFinal Velocity
Final velocity is the speed of an object at the end of a specific time interval or at a particular point in its motion. In the video, the students are trying to determine the final velocity of the ball just before it lands in the bucket. This involves calculating the velocity in both the horizontal and vertical directions and then using vector addition to find the resultant or hypotenuse of the velocity triangle.
๐Ÿ’กVector
A vector is a quantity that has both magnitude and direction. In the context of the video, velocity is a vector quantity because it describes not only how fast the ball is moving but also the direction in which it is moving. The final velocity of the ball is a vector that is found by combining the horizontal and vertical components of velocity.
๐Ÿ’กComponents
In physics, components refer to the individual parts of a vector that are measured along specific axes. In the video, the final velocity in the x and y directions are the components of the resultant vector, which is the overall velocity of the ball. Understanding these components is crucial for solving projectile motion problems.
๐Ÿ’กResultant Vector
A resultant vector is the single vector that represents the combined effect of two or more vectors acting in different directions. In the video, the final velocity of the ball is the resultant vector, which is found by combining the horizontal and vertical components of velocity using the Pythagorean theorem.
๐Ÿ’กPythagorean Theorem
The Pythagorean theorem is a mathematical principle that states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. In the video, this theorem is used to find the magnitude of the final velocity of the ball by considering the horizontal and vertical components of velocity as sides of a right triangle.
๐Ÿ’กInverse Sine
The inverse sine, also known as arcsine, is a mathematical function that gives the angle whose sine is a given value. In the video, the inverse sine is used to find the angle theta, which represents the direction of the final velocity vector relative to the horizontal axis.
๐Ÿ’กDisplacement
Displacement is the change in position of an object and is a vector quantity that includes both magnitude and direction. In the video, displacement is discussed in the context of the ball's horizontal and vertical movement. The ball's horizontal displacement is constant because of its constant horizontal velocity, while its vertical displacement increases due to gravity.
๐Ÿ’กUniformly Accelerated Motion
Uniformly accelerated motion is a type of motion where an object's acceleration remains constant throughout the motion. In the video, the ball experiences uniformly accelerated motion in the vertical direction due to the constant acceleration of gravity. This is in contrast to the horizontal motion, which is at a constant velocity.
Highlights

The problem involves calculating the final velocity of a ball in projectile motion with an initial horizontal velocity.

The final velocity is determined by using the UAM (Velocity, Acceleration, and Mass) equation for the y direction.

The initial velocity in the y direction is zero, and the acceleration is the constant gravitational acceleration (-9.81 m/s^2).

The displacement in the y direction is given as -0.7 meters, indicating a downward motion.

The final velocity in the y direction is calculated to be 3.7 m/s (rounded to two significant figures).

The ball's final velocity in the y direction is negative, indicating it is moving downward.

The final velocity calculation must consider both the x and y components of the motion.

The ball maintains a constant velocity in the x direction of 4.47 m/s.

To find the resultant final velocity, the Pythagorean theorem is applied to the x and y components.

The magnitude of the final velocity is calculated to be 5.80602 m/s, which is rounded to 5.8 m/s with two significant figures.

The final velocity has a direction that needs to be determined, which is done by calculating the angle theta.

The angle theta is found using the inverse sine of the x component velocity divided by the resultant velocity.

The final velocity vector is directed at an angle of approximately 50.3 degrees in front of the negative y axis.

Velocity is a vector quantity, and the calculated magnitude must be considered with its direction.

The ball's velocity vector increases in length as it falls due to the increasing magnitude of its velocity.

The hand remains directly above the ball because both the car and the ball move at the same constant horizontal velocity.

The ball travels farther than the hand because it moves in both x and y directions, while the hand only moves in the x direction.

Projectile motion requires separate analysis for the x and y directions due to different motion characteristics in each.

Transcripts

Browse More Related Video

The Classic Bullet Projectile Motion Experiment

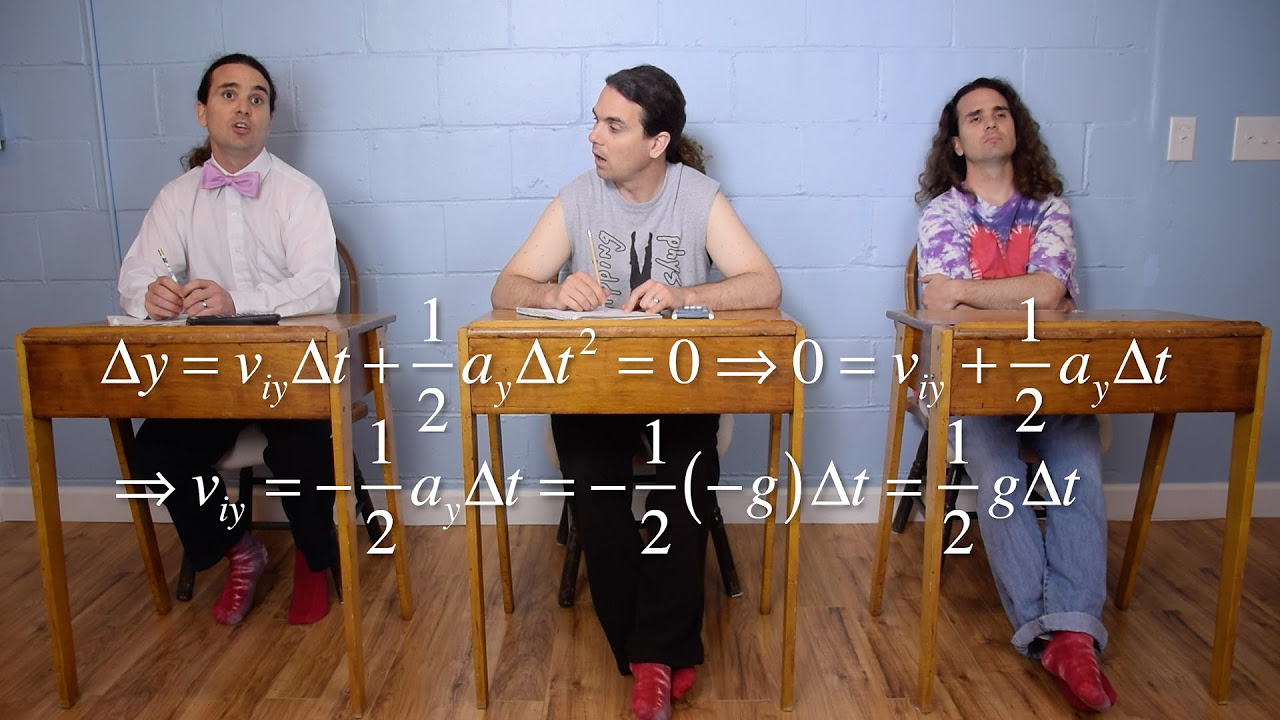
Deriving the Range Equation of Projectile Motion

Introduction to Projectile Motion

(Part 1 of 2) An Introductory Projectile Motion Problem with an Initial Horizontal Velocity

Two Dimensional Motion Problems - Physics

Time of Flight in Projectile Motion | Physics

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics EducationProjectile MotionVelocity CalculationVector AnalysisInteractive LearningTeaching MethodKinematicsClassroom DynamicsMathematics ApplicationScience Experiment