How to Find The Point Where The Graph has a Horizontal Tangent Lines Using Derivatives

The Organic Chemistry Tutor
24 Feb 201808:05
EducationalLearning
32 Likes 10 Comments

TLDRThe video script explains the process of finding points on a graph where the tangent line is horizontal. It emphasizes the importance of understanding that the slope of a horizontal line is zero and demonstrates how to find such points by setting the first derivative of a given function equal to zero and solving for x. The script provides a step-by-step solution for two different functions, showing how to calculate the x-values where the tangent lines are horizontal and how to find corresponding y-values to get the points. This is a comprehensive guide for anyone looking to understand the concept of horizontal tangent lines in the context of calculus.

Takeaways
  • 📈 To find a horizontal tangent line on a graph, the function's first derivative must be set to zero, as horizontal lines have a slope of zero.
  • 🧮 The first step in the process is to calculate the first derivative of the given function.
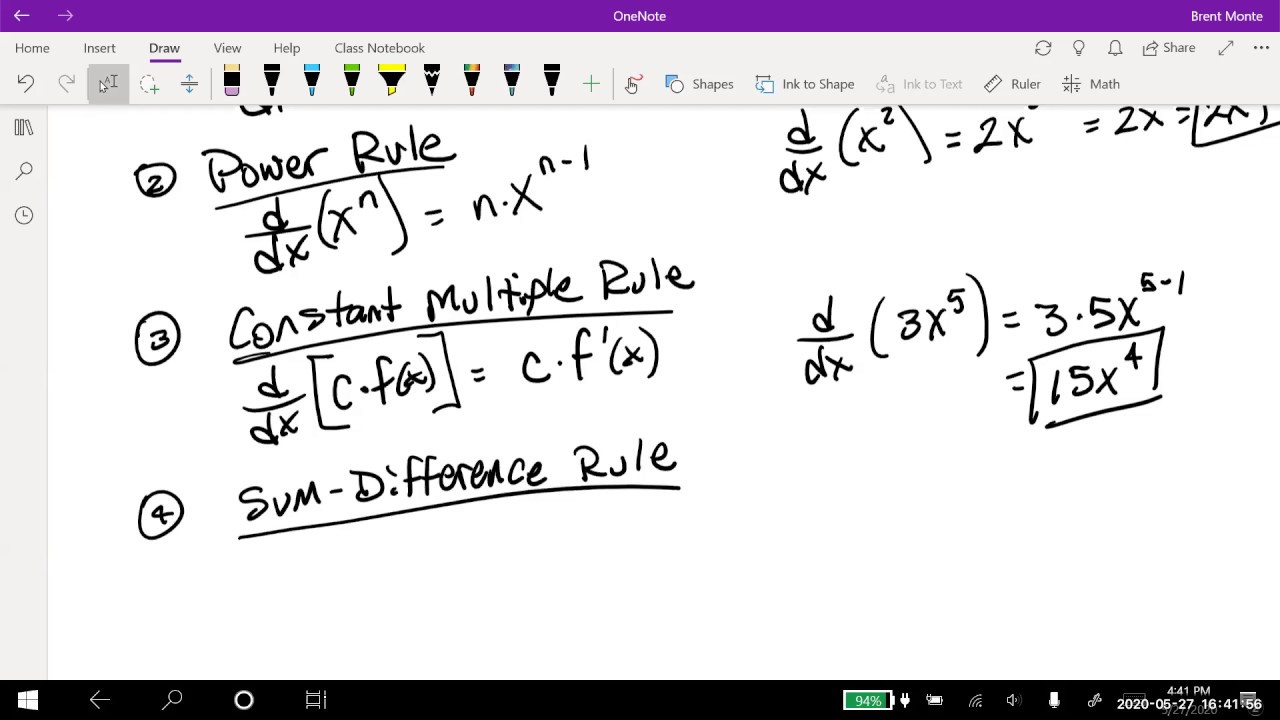
  • 🌟 For the function f(x) = x^3 - 6x^2 + 15, the first derivative is f'(x) = 3x^2 - 12x.
  • 🎯 Setting the first derivative equal to zero helps identify the x-values where the graph has a horizontal tangent line.
  • 📊 Factoring out the greatest common factor (GCF) from the derivative is crucial for solving the equation.
  • 🔢 For the example function, setting 3x^2 - 12x = 0 leads to the solutions x = 0 and x = 4, where horizontal tangent lines occur.
  • 🖼️ Evaluating the function at these x-values gives the corresponding y-values, forming ordered pairs that represent the points of the horizontal tangent lines.
  • 🛠️ For another function, f(x) = 4x^3 - 7x^2 - 6x + 4, the process is similar: find the first derivative and set it to zero to solve for x.
  • 📝 The first derivative for the second function is f'(x) = 12x^2 - 14x - 6, which is then factored to solve for x.
  • 🔍 Factoring involves finding two numbers that multiply to the constant term and add up to the middle coefficient, in this case, -7.
  • 📍 The solutions to the factored equation, 2x = 3 and -3x + 1 = 0, give the x-values of 1.5 and -1/3, where the horizontal tangent lines touch the curve.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is determining the points at which a graph has a horizontal tangent line.

  • How does the video start the explanation?

    -The video starts by explaining the concept of a tangent line and how a horizontal tangent line touches the curve at only one point, as opposed to a secant line which touches at two points.

  • What is the first step in finding the point where a graph has a horizontal tangent line?

    -The first step is to find the first derivative of the given function and set it equal to zero because the slope of a horizontal line is zero.

  • What is the first function given in the video?

    -The first function given in the video is x cubed minus six x squared plus fifteen.

  • What are the factors of the first derivative of the given function?

    -The factors of the first derivative (f prime of x) for the first function are 3x squared and negative 12x.

  • How many points are there where the first function has a horizontal tangent line?

    -There are two points where the first function has a horizontal tangent line, at x equals zero and x equals four.

  • What are the y-values corresponding to the x-values where the first function has horizontal tangent lines?

    -The y-values corresponding to the x-values are 15 for x equals zero and negative 17 for x equals four.

  • What is the second function discussed in the video?

    -The second function discussed in the video is four x cubed minus seven x squared minus six x plus four.

  • How does the video approach factoring the first derivative of the second function?

    -The video approaches factoring the first derivative of the second function by first taking out the greatest common factor (GCF), then focusing on factoring the trinomial 6x squared minus x minus three by grouping and using the cross-multiplication method.

  • What are the x-values where the second function has a horizontal tangent line?

    -The x-values where the second function has a horizontal tangent line are three halves (3/2) and negative one third (-1/3).

  • What is the significance of finding the points where a graph has a horizontal tangent line?

    -Finding the points where a graph has a horizontal tangent line is significant because these points represent the local maximum or minimum values of the function, where the slope of the curve changes from positive to negative or vice versa.

Outlines
00:00
📈 Determining Horizontal Tangent Lines on a Graph

This paragraph discusses the process of finding the points on a graph where the tangent line is horizontal. It begins by explaining the concept of a tangent line and how a horizontal tangent line indicates either a maximum or minimum point on the graph. The speaker then illustrates this by sketching a generic function and explaining that to find such points, one must calculate the first derivative of the given function and set it equal to zero (since the slope of a horizontal line is zero). Using the function f(x) = x^3 - 6x^2 + 15 as an example, the speaker calculates its first derivative, f'(x) = 3x^2 - 12x, and sets it equal to zero to find the x-values where the graph has horizontal tangent lines. By factoring and solving the equation, the speaker finds the x-values to be 0 and 4. The paragraph concludes with the speaker calculating the corresponding y-values to form ordered pairs for these points, which are (0, 15) and (4, -17), indicating the locations of the horizontal tangent lines on the graph.

05:02
📊 Factoring and Solving for Horizontal Tangent Points

The second paragraph continues the discussion on finding points where a graph has horizontal tangent lines, using a different function as an example. The function given is f(x) = 4x^3 - 7x^2 - 6x + 4. The speaker explains the process of finding the first derivative and setting it equal to zero to locate the points of interest. The derivative calculated is f'(x) = 12x^2 - 14x - 6. The speaker then moves on to factor the quadratic equation, explaining the steps in detail, including finding the greatest common factor (GCF) and using factoring by grouping. The factored form leads to two linear equations, which when solved, yield the x-values of 3/2 and -1/3. The speaker mentions that one could find the corresponding y-coordinates but decides to stop at this point, concluding the video with these findings.

Mindmap
Keywords
💡Derivative
The derivative is a fundamental concept in calculus that represents the rate of change or the slope of a function at a particular point. In the context of the video, the derivative is used to find the slope of the tangent line to the graph of a function. By setting the derivative equal to zero, we can determine the points where the tangent line is horizontal, as a horizontal line has a slope of zero.
💡Tangent Line
A tangent line is a line that touches a curve at a single point without crossing it. In the video, the focus is on finding the points where the graph of a given function has a horizontal tangent line, which means the slope of the tangent at that point is zero. This is important for understanding the behavior of the function and its graph, such as identifying local maxima or minima.
💡Slope
Slope is a measure of the steepness of a line, indicating the rate of change between the y and x values. A line with a slope of zero is horizontal, which is significant in the video because the goal is to find points where the graph of a function has a horizontal tangent line, indicating a slope of zero at those points.
💡Factoring
Factoring is the process of breaking down a polynomial into its constituent factors, which are expressions that multiply together to give the original polynomial. In the video, factoring is used as a method to solve for x when setting the derivative of a function equal to zero, in order to find the points where the graph has a horizontal tangent line.
💡Graph
A graph is a visual representation of the relationship between variables, typically with a coordinate system where each point represents a pair of values that satisfy the equation of the function. In the video, the graph of a function is analyzed to find the points where it has a horizontal tangent line, which corresponds to the maximum or minimum points on the curve.
💡Horizontal Line
A horizontal line is a straight line on a graph where the y-values are constant, meaning the slope is zero. In the context of the video, identifying horizontal tangent lines is crucial for finding points on a function's graph where the slope is zero, which can indicate important features such as local maxima or minima.
💡Ordered Pair
An ordered pair is a pair of numbers that specifies a point in a coordinate system, with the first number typically representing the x-coordinate and the second number representing the y-coordinate. In the video, ordered pairs are used to describe the points where the graph of a function has a horizontal tangent line, providing both the x and y values for these points.
💡Local Maximum/Minimum
Local maximum or minimum refers to a point on a graph where the function reaches a peak or valley in a small neighborhood, but not necessarily the entire graph. Horizontal tangent lines often occur at these points, as the slope of the function changes from positive to negative (local maximum) or vice versa (local minimum), indicating a change in the function's behavior.
💡Set to Zero
Setting to zero is a common mathematical technique used to solve equations, particularly in calculus when finding critical points or determining the behavior of a function. In the video, setting the derivative of a function to zero is a key step in finding the points where the graph has a horizontal tangent line, as this process reveals the x-values where the function's slope is zero.
💡Greatest Common Factor (GCF)
The greatest common factor (GCF) is the largest factor that two or more numbers share, which can be used to simplify expressions or polynomials by factoring out this common factor. In the video, the GCF is used to simplify the derivative of the function when setting it equal to zero, making it easier to solve for x and find the horizontal tangent lines.
💡Factor by Grouping
Factor by grouping is a technique used in algebra to factor a quadratic trinomial by grouping terms in pairs and factoring out the greatest common factor from each pair. This method is particularly useful when the trinomial does not factor easily or when the GCF is not immediately apparent. In the video, this technique is applied to the derivative of the second function to find the x-values for the horizontal tangent lines.
Highlights

The method to determine the point at which a graph has a horizontal tangent line is discussed.

A horizontal tangent line occurs at a maximum or minimum point on the graph.

The slope of a horizontal line is zero, which is key to finding a horizontal tangent line.

To find a horizontal tangent line, set the first derivative of the function equal to zero.

The first derivative of x cubed is 3x squared, and for x squared is 2x.

For the given function x cubed minus six x squared plus fifteen, the first derivative is 3x squared minus 12x.

Solving the first derivative equation, 3x squared minus 12x, results in x values of zero and four.

The ordered pair for the first point where the horizontal tangent line occurs is (0, 15).

The ordered pair for the second point where the horizontal tangent line occurs is (4, -17).

The process is demonstrated with a second function, f(x) = 4x cubed minus seven x squared minus six x plus four.

The first derivative for the second function is 12x squared plus 14x minus 6.

Factoring the first derivative of the second function leads to the factors (6x plus 3) and (2x minus 1).

The x values for the second function where the horizontal tangent line occurs are three halves and negative one third.

The method explained is useful for understanding the behavior of functions and their graphs.

This mathematical process can be applied to various real-world problems involving optimization.

The video provides a clear and detailed explanation of how to find horizontal tangent lines on a graph.

The use of examples and step-by-step instructions makes the concept accessible to learners.

The video demonstrates the importance of understanding derivatives in calculus.

The method can be used to find points of inflection and other critical points on a curve.

Transcripts

Browse More Related Video

Finding Stationary Points and Determining their Nature

Finding Local Maximum and Minimum Values of a Function - Relative Extrema

Finding Intersections of Functions (Precaluclus - College Algebra 22)

Math 11 - Section 1.5

How To Find The Equation of the Normal Line

Relative Maxima/Minima Examples

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusDerivativesTangent LinesSlope AnalysisMath EducationGraph SketchingZero Slopex-coordinatesTrigonometry