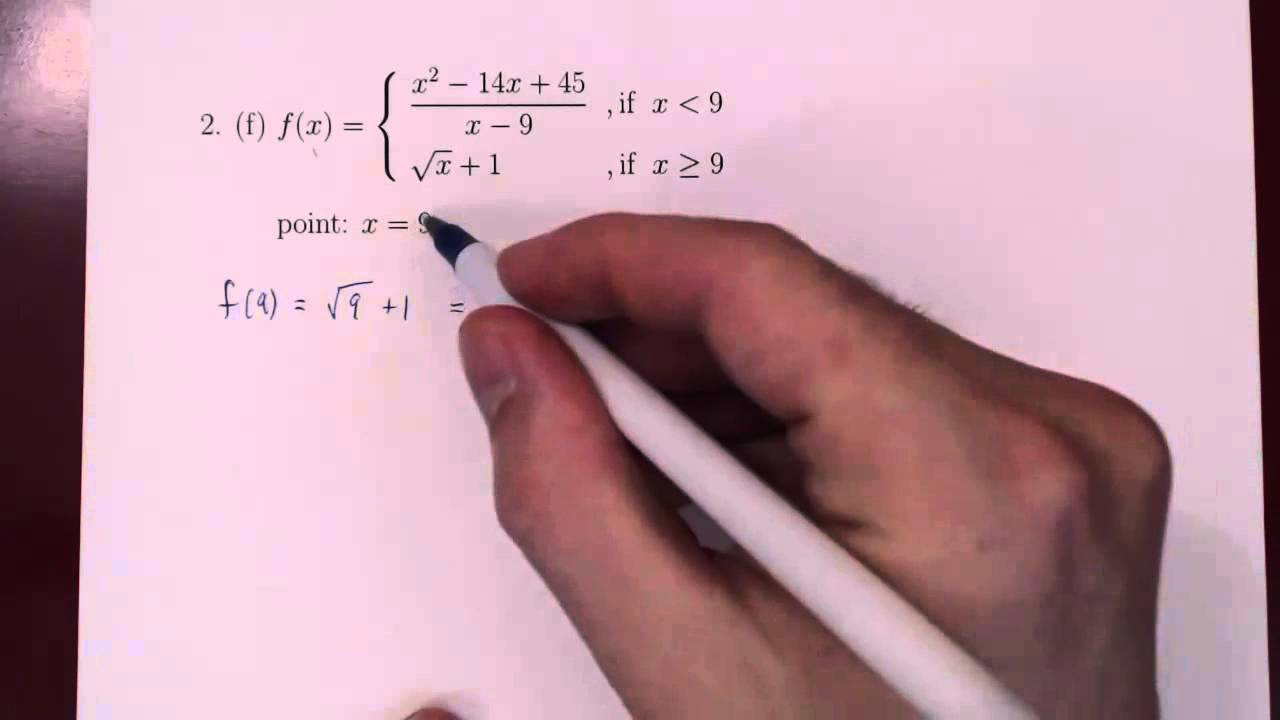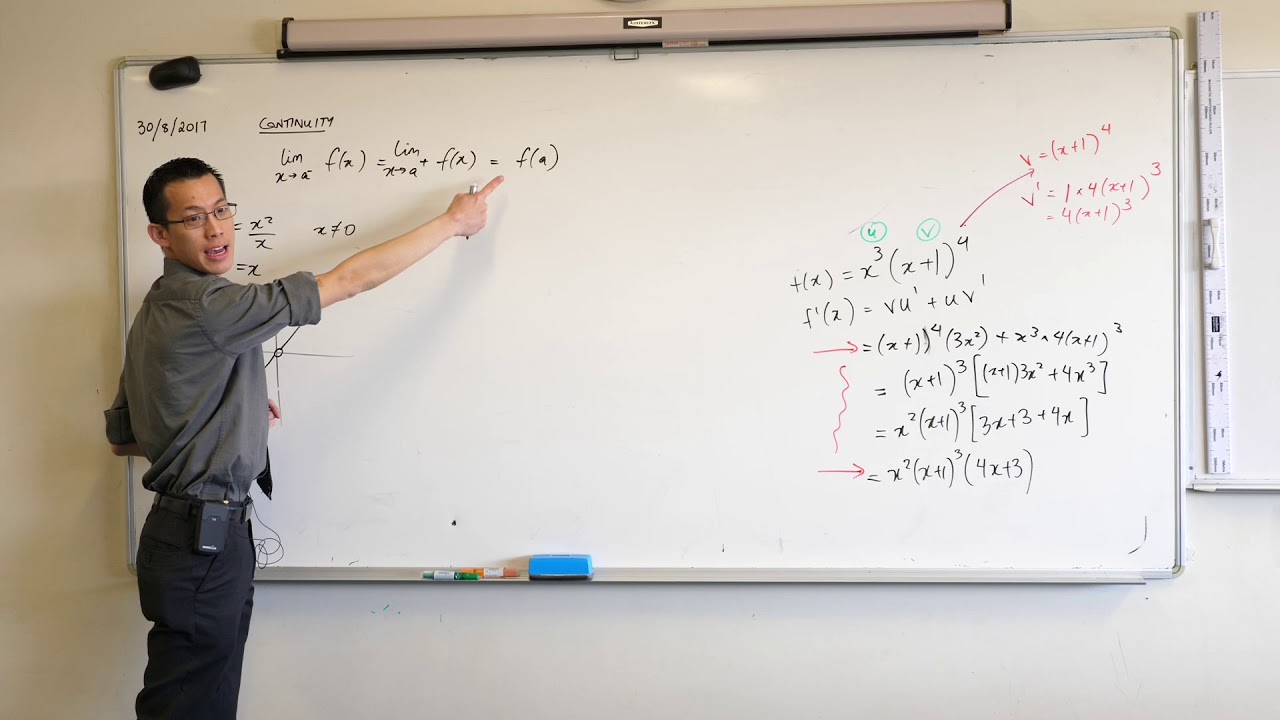Continuity at a point | Limits and continuity | AP Calculus AB | Khan Academy
TLDRThe video script delves into the concept of continuity in functions, transitioning from an intuitive understanding where a function appears connected without lifting the pen to a formal definition. It explains that a function f is continuous at a point x=c if the limit of f(x) from both directions equals f(c). The script uses examples to illustrate scenarios where functions are continuous and where there are points of discontinuity, reinforcing the concept with visual and intuitive analogies.
Takeaways
- 📌 The concept of continuity in functions is formally defined as a function being continuous at a point if the two-sided limit of the function as x approaches that point is equal to the function's value at that point.
- 🖋️ The informal or intuitive definition of continuity is that you can draw the graph of the function at a point without lifting your pen.
- 📈 For a function to be considered continuous at a point c, the limit from both the left and the right must equal the value of the function at c.
- 🚫 A function with a jump or discontinuity at a point c, where the limit from the left and right do not equal the function's value at c, is not continuous at that point.
- 🔄 The formal definition of continuity requires a two-sided limit, meaning the limit as x approaches c from both the left and the right.
- 📊 Examples in the script illustrate that even if the limit exists, if it does not match the function's value at c, the function is discontinuous at that point.
- 🤔 The script encourages critical thinking by comparing the intuitive 'pick up the pencil' test with the more rigorous mathematical definition of continuity.
- 🌐 The concept of continuity is fundamental in calculus and mathematical analysis, as it helps in understanding the behavior of functions and their graphs.
- 🔢 The formal definition of continuity is essential for mathematical rigor and is used to prove theorems and solve problems in calculus.
- 📚 The script serves as an educational resource for understanding the concept of continuity, providing both the intuitive understanding and the formal mathematical definition.
- 🎓 The instructor's explanation aims to clarify the transition from an intuitive understanding to a formal mathematical definition, which is crucial for advanced study in mathematics.
Q & A
What is the intuitive idea of continuity in a function?
-The intuitive idea of continuity in a function is that you can draw the graph of the function at a certain point without lifting your pencil, indicating a smooth and connected graph without any jumps or breaks.
What does it mean to have a function that is continuous at a point?
-A function is said to be continuous at a point if the two-sided limit of the function as the independent variable approaches that point is equal to the value of the function at that point.
What is the formal definition of continuity for a function at a point x=c?
-The function f is continuous at x=c if, and only if, the two-sided limit of f(x) as x approaches c is equal to f(c). This means that the limit from the left and the limit from the right both converge to the same value as the function's value at c.
How can we determine if a function is continuous at a point using the intuitive method?
-Using the intuitive method, we can determine if a function is continuous at a point by observing if we can draw the graph of the function at that point without lifting our pencil. If the graph is unbroken and connected, the function is considered continuous at that point.
What is a point discontinuity?
-A point discontinuity occurs when there is a sudden jump or break in the graph of a function at a certain point. In this case, the function is not continuous at that point because the two-sided limit as x approaches the point of discontinuity does not equal the function's value at that point.
How does the formal definition of continuity help us understand point discontinuities?
-The formal definition of continuity helps us understand point discontinuities by focusing on whether the two-sided limit as x approaches the point of interest equals the function's value at that point. If the two-sided limit exists but is different from the function's value, or if the two-sided limit does not exist, we have a point discontinuity.
What happens when the two-sided limit at a point does not exist?
-When the two-sided limit at a point does not exist, the function is not continuous at that point. This situation indicates that the function's graph would require lifting the pencil to continue drawing, as the function's behavior from both the left and the right approaches the point is not consistent.
What is the relationship between the intuitive method and the formal definition of continuity?
-The intuitive method provides a visual way to understand continuity by observing the graph of a function, while the formal definition provides a mathematical framework to precisely determine continuity. Both methods aim to assess whether the function's value and its limits from all directions at a point are consistent and connected.
How can we use the concept of continuity to analyze the behavior of a function at a specific point?
-By applying the concept of continuity, we can analyze the behavior of a function at a specific point by checking if the two-sided limit as x approaches that point equals the function's value at that point. If they are equal, the function is continuous and behaves smoothly at that point; if not, the function has a discontinuity.
What is the significance of a function being continuous over an interval?
-The significance of a function being continuous over an interval is that the function's graph is unbroken and connected throughout that interval, which allows for reliable predictions and analysis of the function's behavior without worrying about abrupt changes or breaks in the graph.
Outlines
📚 Introduction to Continuity in Functions
This paragraph introduces the concept of continuity in functions, starting with an intuitive understanding that a function is continuous at a point if its graph can be drawn without lifting the pencil. The instructor explains that this idea is not rigorous and proposes a more formal definition of continuity. The formal definition states that a function f is continuous at a point x=c if and only if the two-sided limit of f(x) as x approaches c is equal to f(c). The paragraph also discusses the importance of this definition in understanding the behavior of functions at specific points and sets the stage for examining examples that illustrate different types of continuity.
🔍 Analyzing Continuity with Examples
In this paragraph, the instructor delves into examples that demonstrate the concept of continuity. The first example shows a function that appears to be continuous at a point x=c, as there are no jumps or discontinuities. The two-sided limit from both the left and the right approaches the value of the function at c, confirming its continuity. The paragraph then explores a scenario with a point discontinuity, where the limit as x approaches c from the left and right does not match the value of the function at c, indicating a discontinuity. Another example is given where the two-sided limit does not exist, further illustrating a lack of continuity. The discussion reinforces the importance of the formal definition of continuity and how it aligns with the intuitive 'pick-up-the-pencil' test.
Mindmap
Keywords
💡Continuity
💡Function
💡Graph
💡Limit
💡Two-sided limit
💡Point discontinuity
💡Pencil test
💡Rigorous definition
💡Value of the function
💡Existence of the limit
💡Formal terminology
Highlights
The video aims to provide a rigorous definition for continuity in functions.
The intuitive idea of continuity is that a function can be drawn without lifting the pen from the paper.
Continuity at a point is defined by the two-sided limit of the function being equal to the function's value at that point.
The formal definition of continuity involves the limit from both the left and the right approaching the function's value at a specific point.
An example is provided where the function appears continuous as there are no jumps or discontinuities.
The limit from the left approaches the function's value at a point c, which seems to indicate continuity.
A point discontinuity is introduced as a scenario where the function is not continuous.
In a point discontinuity, the two-sided limit exists but is different from the function's value at the point of discontinuity.
A scenario is discussed where the two-sided limit does not exist, indicating a lack of continuity.
The video compares the intuitive 'pick up the pencil' test with the rigorous definition of continuity.
The 'pick up the pencil' test aligns with the rigorous definition when the two-sided limit does not exist.
Even when the two-sided limit exists, if it differs from the function's value, the function is not continuous.
Continuity is achieved only when the two-sided limit matches the function's value at a given point.
The video emphasizes the importance of the two-sided limit for the continuity of a function.
The discussion includes practical applications of the continuity definition in analyzing function graphs.
The video concludes by reinforcing that continuity is confirmed when the two-sided limit equals the function's value.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: