Connecting limits and graphical behavior | Limits and continuity | AP Calculus AB | Khan Academy
TLDRThe video script discusses the concept of limits in calculus, emphasizing that limits describe the behavior of a function as it approaches a certain point, but do not reveal the exact value of the function at that point. It illustrates this with the example of a function g(x) approaching negative six as x approaches five, highlighting that different functions can share the same limit at a point but have entirely different forms. The script also mentions that limits can be taken at numerous points, not just where discontinuities occur, offering a broader perspective on the application of limits in understanding function behavior.
Takeaways
- 📈 The concept of a limit is introduced as a way to understand the behavior of a function as it approaches a certain value of x.
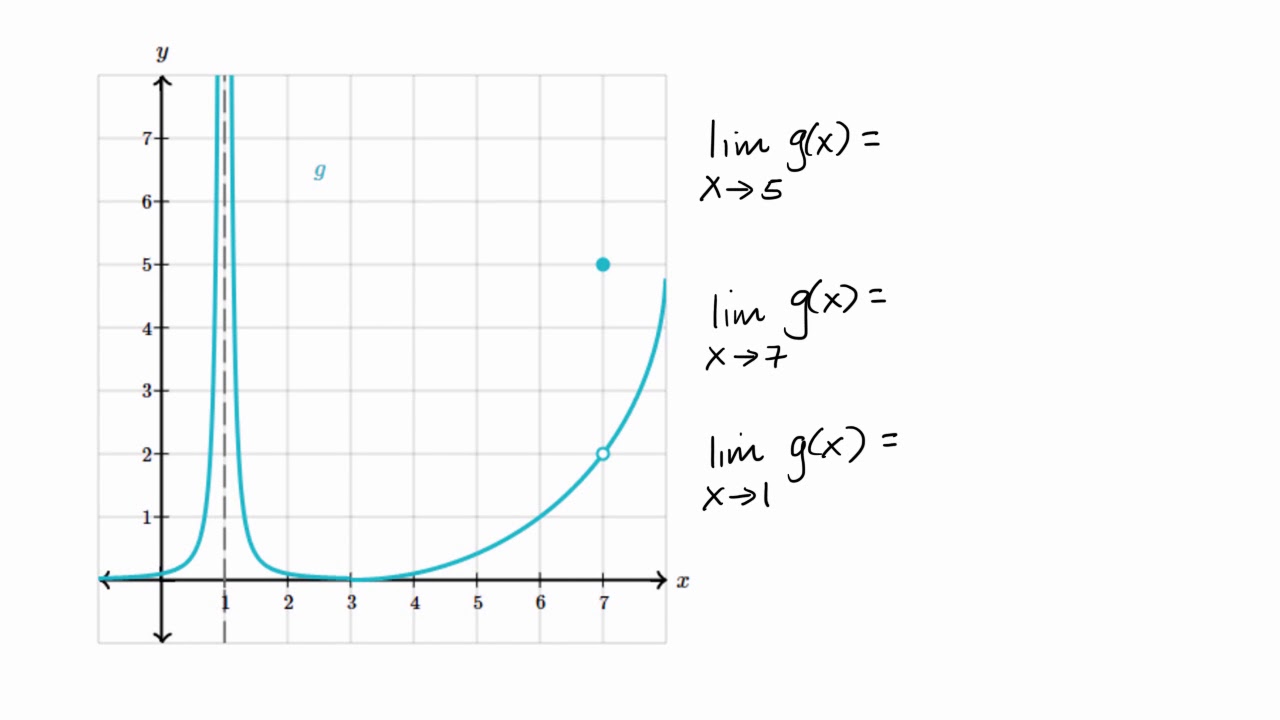
- 🔍 For the function g(x), as x approaches 5, the value of g(x) approaches -6 from both the left and the right.
- 🚫 It's clarified that the limit does not equal g(5), but rather describes the behavior of the function near that point.
- 🌟 The video emphasizes that a limit describes the behavior of a function, not the exact value at the point of interest.
- 🤔 The idea of constructing different functions with the same limit at a point is presented, highlighting the variety of functions that can have the limit of -6 as x approaches 5.
- 🎨 An example is given where the function f(x) has the same limit as g(x) at x=5, but could look very different from g(x).
- 🤝 The video encourages the viewer to pause and attempt to sketch their own functions with the same limit at a point.
- 📌 The concept of limits at different points of a function is discussed, using x=1 and x=π as examples.
- 🔄 The video shows that as x approaches 1, the limit is equal to g(1), and similarly for x=π, the limit is g(π).
- 📈 The importance of understanding that limits can be taken at many points, not just where discontinuities or 'strange' behavior occurs, is emphasized.
Q & A
What is the main concept being discussed in the video?
-The main concept discussed in the video is the idea of limits in mathematics, specifically how they describe the behavior of a function as it approaches a certain point, without necessarily providing information about the function's value at that point.
What is the limit of the function g(x) as x approaches 5, according to the video?
-The limit of the function g(x) as x approaches 5 is negative six, both from the left and from the right.
What is the difference between the limit of a function and the value of the function at a specific point?
-The limit of a function describes how the function behaves as it gets closer to a certain point, while the value of the function at a specific point is the actual output of the function when you plug that point into the function.
Can multiple functions have the same limit at a point?
-Yes, multiple functions can have the same limit at a point. The video provides examples of different functions that all have a limit of negative six as x approaches 5, but look very different from each other.
How does the video illustrate the concept of limits with different functions?
-The video illustrates the concept of limits by showing that different functions, such as f(x) and h(x), can have the same limit of negative six as x approaches 5, despite their different appearances and definitions.
What is the limit of g(x) as x approaches 1 according to the video?
-The limit of g(x) as x approaches 1 is equal to g(1), which is approximately negative 5.1 based on the graph shown in the video.
What is the limit of g(x) as x approaches pi as shown in the video?
-The limit of g(x) as x approaches pi is equal to g(pi), since there are no discontinuities or other interesting features at that point.
What are the two key takeaways from the video?
-The two key takeaways are that many different functions can have the same limit at a point, and for a given function, you can take the limit at many different points, even an infinite number of them.
Why is it important to understand the difference between a function's limit and its value at a point?
-Understanding the difference is important because it helps to appreciate the behavior of a function near certain points without assuming the function's exact value at those points. This is crucial for accurate analysis and prediction of the function's behavior.
How does the video demonstrate the concept of limits at points where there are no discontinuities?
-The video demonstrates this concept by showing that even at points where there are no discontinuities, such as pi in the example, the limit can still be taken and it will be equal to the function's value at that point.
What is the significance of discussing limits at 'interesting' points in a function?
-Discussing limits at 'interesting' points, such as points of discontinuity or where the function behaves unusually, helps to understand the function's behavior and properties more deeply, and can reveal important characteristics of the function that might not be evident from looking at the function's overall graph.
Outlines
📊 Understanding Limits and Function Behavior
This paragraph discusses the concept of limits in the context of a function, specifically focusing on the behavior of the function g(x) as x approaches the value of 5. The instructor explains that the limit describes the function's behavior as it nears a certain point, but does not provide information about the function's value at that point. The video emphasizes that different functions can have the same limit at a point, as demonstrated by the hypothetical functions f(x) and h(x), which both approach a limit of negative six as x approaches five. The key takeaway is that limits can be taken at many different points and that limits are about the function's approach to a point rather than the point itself.
Mindmap
Keywords
💡limit
💡function
💡graph
💡approaches
💡discontinuity
💡negative six
💡f(x)
💡circle
💡pi
💡behavior
💡value
Highlights
Introduction to the concept of limits using the graph of y = g(x).
Explanation of approaching a limit from the left and the right sides.
Establishing that as x approaches 5, g(x) approaches -6.
Clarification that a limit describes the behavior of a function as it approaches a point, not the function's value at that point.
Differentiation between the limit of g(x) as x approaches 5 and the value of g(5).
Illustration of how different functions can have the same limit at a specific point.
Challenge to create a function with the same limit as g(x) as x approaches 5, showcasing the versatility of limits.
Introduction of function f(x) and its behavior as it approaches the limit from both sides.
Description of another function, h(x), with the same limit approaching from both sides but with a different overall behavior.
Emphasis on the diversity of functions that can share the same limit at a particular point.
Explanation of point discontinuity and its significance in understanding limits.
Demonstration of calculating limits at various points, including points of continuity.
Example of finding the limit of g(x) as x approaches 1 and its practical implication.
Exploration of the limit of g(x) as x approaches pi, illustrating limits at infinite points.
Conclusion highlighting the importance of limits, especially at points where the function behaves unusually.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: