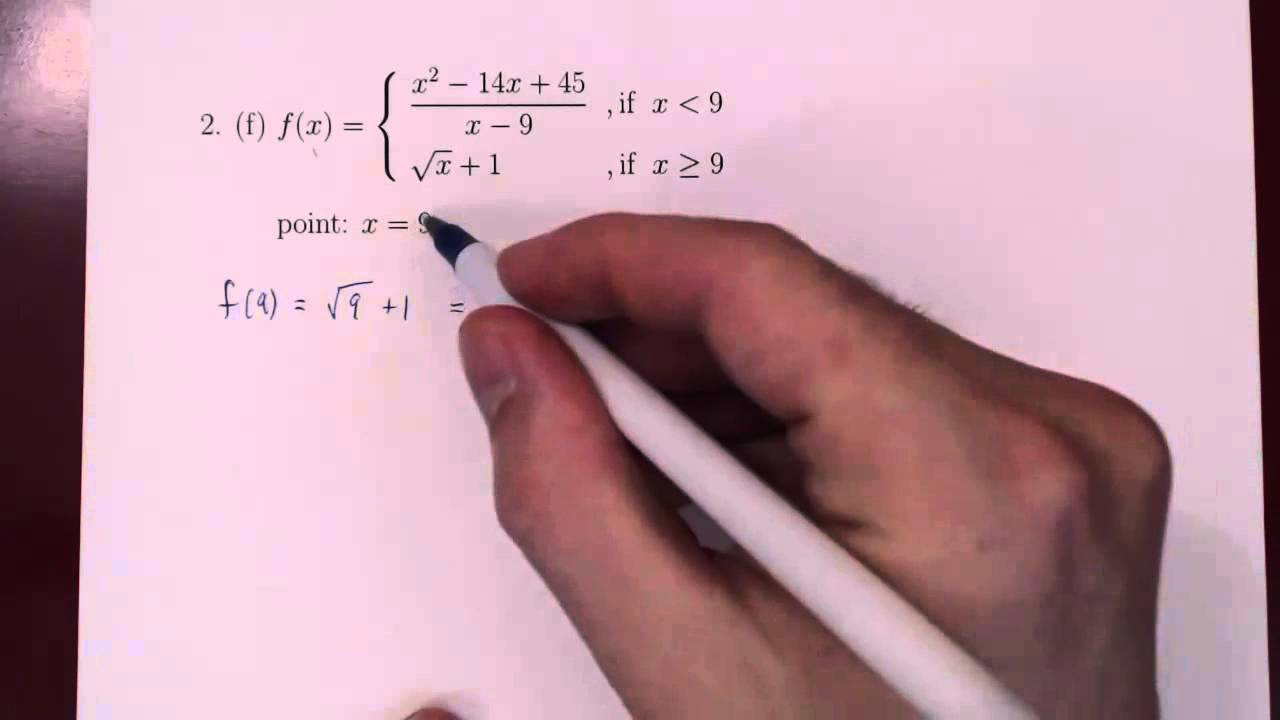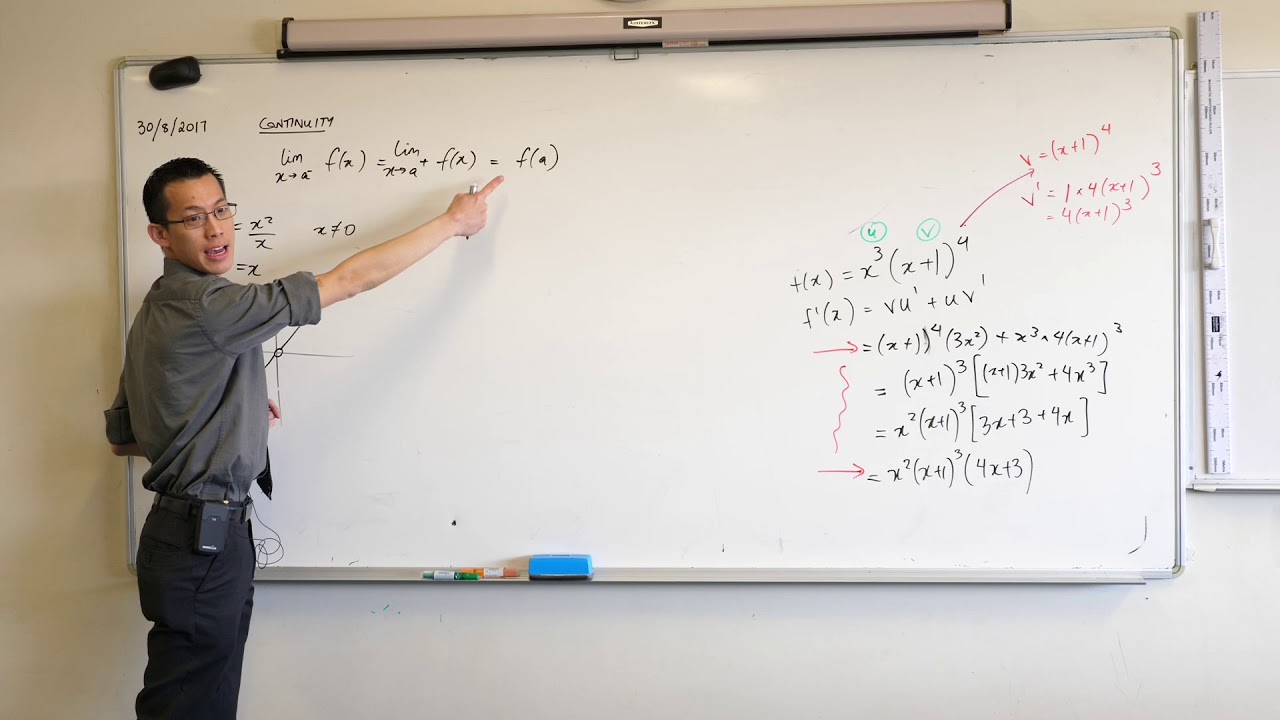2011 Calculus AB free response #6a | AP Calculus AB | Khan Academy
TLDRThe video script discusses the continuity of a piecewise function, f(x), at x=0. It explains that for a function to be continuous, the limit from the left and the right as x approaches 0 must equal the function's value at 0. By evaluating the function at x=0 and calculating the limits from both sides, the script demonstrates that f(x) is indeed continuous at x=0, as all values are found to be equal to 1.
Takeaways
- 📌 The function f(x) is defined with two distinct cases based on the value of x.
- 🔍 For x ≤ 0, f(x) = 1 - 2sin(x), and for x > 0, f(x) = e^(-4x).
- 🌟 The continuity of f(x) at x = 0 is the focus of the problem.
- 🤔 Continuity requires that the limit from the left equals the limit from the right, and both equal the function's value at that point.
- 📈 The sine function is used in the definition of f(x) for x ≤ 0.
- 📊 The limit of f(x) as x approaches 0 from the left is evaluated using the properties of the sine function.
- 📂 The limit from the left is found to be 1, as sin(0) = 0 and e^(-4*0) = 1.
- 🧠 For x > 0, the function f(x) utilizes the exponential function e^(-4x).
- 📈 The limit of f(x) as x approaches 0 from the right is also evaluated, resulting in the same value of 1.
- 🔗 The value of f(0) is calculated to be 1, using the definition of f(x) for x ≤ 0.
- 🎯 All calculated values (f(0), limit from left, and limit from right) are equal to 1, confirming the continuity of f(x) at x = 0.
Q & A
What is the definition of function f(x) for x ≤ 0?
-For x less than or equal to 0, the function f(x) is defined as 1 minus 2 times the sine of x.
How is function f(x) defined for x > 0?
-For x greater than 0, f(x) is defined as e to the power of negative 4x.
What does it mean for a function to be continuous at a certain point?
-A function is continuous at a certain point if the limit of the function as x approaches that point from the left is equal to the function's value at that point and also equal to the limit as x approaches from the right.
What is the value of f(0) according to the given definition?
-The value of f(0) is 1, since sine of 0 is 0, and thus 1 minus 2 times 0 equals 1.
How do we determine the limit of f(x) as x approaches 0 from the left?
-The limit of f(x) as x approaches 0 from the left is the same as the value of f(0) because the function's definition for x ≤ 0 applies, which we've determined to be 1.
What is the limit of e to the negative 4x as x approaches 0 from the right?
-The limit of e to the negative 4x as x approaches 0 from the right is 1, since any number to the power of 0 is 1.
How does the continuity of the sine function and the exponential function play a role in this problem?
-Both the sine function and the exponential function are continuous, which ensures that the limits as x approaches 0 from the left and from the right exist and can be equated to the function's value at 0.
What would happen if the function's value at a point was not equal to the limits approaching that point from the left and right?
-If the function's value at a point was not equal to the limits approaching that point, the function would not be continuous at that point, potentially creating a gap in the graph.
How can we verify the continuity of f(x) at x = 0 using the given information?
-By showing that the value of f(0), the limit of f(x) as x approaches 0 from the left, and the limit as x approaches 0 from the right are all equal to 1, we can verify that f(x) is continuous at x = 0.
What is the significance of a function being continuous over an interval?
-A function being continuous over an interval means that there are no gaps, jumps, or breaks in the graph of the function within that interval, which is important for many mathematical and practical applications.
What other properties or characteristics of functions might be relevant when studying continuity?
-Other relevant properties when studying continuity include differentiability, integrability, and the existence of limits at every point within the interval, all of which contribute to a thorough understanding of the function's behavior.
Outlines
📚 Continuity of Function f at x=0
This paragraph discusses the continuity of a function, f, at x=0. The function is defined with two cases: when x ≤ 0, f(x) = 1 - 2sin(x), and when x > 0, f(x) = e^(-4x). The main objective is to demonstrate that f is continuous at x=0. This requires showing that the left-hand limit and the right-hand limit of f(x) as x approaches 0 are equal to the value of f(0). The explanation includes a visual representation of the function and its behavior around x=0, emphasizing the importance of the function's value and the limits matching for continuity. The sine function's continuity is utilized to evaluate the left-hand limit, which is found to be 1. Similarly, the right-hand limit is evaluated using the exponential function's properties, also resulting in 1. Since both limits and the function's value at x=0 are equal, it is concluded that the function f is continuous at x=0.
Mindmap
Keywords
💡Continuous Function
💡Piecewise Function
💡Limit
💡Sine Function
💡Exponential Function
💡Approaching from the Left
💡Approaching from the Right
💡Function Value at a Point
💡Gap
💡Continuous at x = 0
Highlights
The function f(x) is defined with two cases based on the value of x.
For x ≤ 0, f(x) = 1 - 2sin(x).
For x > 0, f(x) = e^(-4x).
The task is to demonstrate the continuity of f(x) at x = 0.
Continuity at x = 0 requires the left and right limits to equal the function's value at that point.
The limit from the left for f(x) when x approaches 0 is 1 - 2sin(0), which equals 1.
The sine function is continuous, which helps in determining the limit from the left.
The limit from the right for f(x) as x approaches 0 is e^(-4*0), which equals 1.
The exponential function used in the second case is also continuous.
The value of f(0) is calculated as 1 - 2sin(0), resulting in 1.
The function's value at x = 0 matches the limits from both the left and the right.
The continuity of f(x) at x = 0 is confirmed by the equality of the function's value and its limits.
A gap in the function's value and its limits would indicate discontinuity.
The concept of limits is crucial for determining continuity.
The transcript provides a step-by-step analysis of the function's continuity at a specific point.
The mathematical concepts of continuity, limits, and the properties of sine and exponential functions are central to the discussion.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: