Watch me solve this 4th degree polynomial equation
TLDRIn this educational video, math instructor John explains how to solve a fourth-degree polynomial equation, a^4 + a^2 - 6 = 0, without revealing its type initially. He emphasizes the importance of recognizing the equation's nature and applying the fundamental theorem of algebra to determine the number of solutions. John demonstrates the process of solving the equation using substitution and factoring techniques, leading to four unique solutions, including complex numbers. He also discusses the necessity of mastering basic algebraic concepts to succeed in more advanced math courses.
Takeaways
- 📚 The video is a tutorial on solving a specific equation without revealing its type, aiming to engage viewers in problem-solving.
- 🧐 The equation given is a fourth-degree polynomial equation: a^4 + a^2 - 6 = 0.
- 🤔 The video challenges viewers to solve the equation before revealing the answer and explanation.
- 🎓 The instructor, John, has decades of experience teaching middle and high school math and aims to simplify math learning.
- 🏫 The video is particularly relevant for students taking advanced math courses like Algebra 2, college algebra, or pre-algebra.
- 📈 The solution to the equation is a = ±√3i and a = ±√2, involving both real and complex (imaginary) solutions.
- 🌟 The video emphasizes the importance of understanding the type of equation and the fundamental theorem of algebra in solving polynomial equations.
- 📝 Polynomial equations can be of any degree and require different techniques based on the degree and nature of the equation.
- 🔍 The video introduces the concept of substitution as a method for solving polynomial equations by transforming them into simpler forms.
- 🛠️ Factoring is highlighted as a crucial skill for solving polynomial equations, and the video suggests strengthening this skill for better problem-solving.
- 📚 The instructor offers further assistance through his math program at TCM Academy for those needing more help in mathematics.
Q & A
What is the main topic of the video?
-The main topic of the video is solving a fourth-degree polynomial equation.
What is the equation that needs to be solved?
-The equation that needs to be solved is a^4 + a^2 - 6 = 0.
How many unique solutions does the equation have?
-The equation has four unique solutions, two real and two complex or imaginary.
What is the significance of the Fundamental Theorem of Algebra mentioned in the video?
-The Fundamental Theorem of Algebra states that the number of solutions to a polynomial equation is equal to the degree of the polynomial. In this case, since it's a fourth-degree polynomial, there will be four solutions.
What method is used to solve the given polynomial equation?
-The method used to solve the given polynomial equation is factoring by substitution.
What are the two complex or imaginary solutions of the equation?
-The two complex or imaginary solutions are ±√3i.
What are the two real solutions of the equation?
-The two real solutions are ±√2.
Why does the instructor emphasize the importance of understanding factoring?
-The instructor emphasizes the importance of understanding factoring because it is a fundamental skill that makes solving polynomial equations much easier and is essential for success in higher levels of mathematics.
What advice does the instructor give to students who are struggling with the material?
-The instructor advises students to go back and strengthen their foundational skills, such as factoring and understanding complex numbers, as there are no shortcuts in advanced mathematics.
How can students access more comprehensive instruction on the topics covered in the video?
-Students can access more comprehensive instruction by checking out the instructor's courses on his website, TCM Academy.com, which cover a range of math topics from basic math to calculus.
Outlines
🔍 Introduction to Solving an Unknown Equation
The speaker, John, introduces the video by stating the intention to solve an unspecified equation without revealing its type. He encourages viewers to attempt solving the equation first and shares the correct answer later. John also briefly discusses his background in teaching math and promotes his math program at TCM academy. The equation given is a fourth-degree polynomial equation, and the correct solutions include both real and imaginary numbers.
📚 Understanding Polynomial Equations
John explains what a polynomial equation is, emphasizing the importance of understanding the type of equation being dealt with. He describes the components of a polynomial, including the variable, coefficients, and powers. The speaker also introduces the fundamental theorem of algebra, which states that the number of solutions to a polynomial equation is equal to its highest power. He uses examples to illustrate different types of equations and their solutions.
🧠 Factoring and Substitution for Solving Equations
The speaker discusses the concept of factoring as a primary method for solving polynomial equations. He introduces the technique of substitution to simplify the given fourth-degree polynomial equation. John demonstrates how to rewrite the equation using substitution and factor it into a quadratic trinomial, which can then be solved more easily. He emphasizes the importance of recognizing patterns in equations to apply the correct methods.
🔢 Solving the Substituted Equation
John continues by solving the substituted quadratic trinomial equation. He factors it into two binomials and applies the zero product property to find the solutions for the substituted variable U. The speaker then explains that these solutions for U are not the final answers but are necessary steps to solve the original equation. He also addresses the importance of subscribing to his YouTube channel for further math assistance.
🎓 Returning to the Original Equation and Final Thoughts
The speaker substitutes back the original variable 'a' for 'U' to find the solutions to the original fourth-degree polynomial equation. He explains how to handle the complex solutions and emphasizes the importance of understanding complex numbers. John concludes by offering advice on overcoming math challenges, suggesting that viewers strengthen their foundational math skills and consider his courses for further learning. He ends the video by wishing viewers well in their mathematical endeavors.
Mindmap
Keywords
💡Equation
💡Variable
💡Polynomial
💡Algebra
💡Solving
💡Substitution
💡Factoring
💡Fundamental Theorem of Algebra
💡Complex Numbers
💡Educational Content
Highlights
The video aims to teach viewers how to solve a specific equation without revealing its type, allowing the audience to attempt solving it first.
The equation being solved is \(a^4 + a^2 - 6 = 0\), where the goal is to solve for the variable \(a\).
The correct answer to the equation reveals four unique solutions, including both real and complex numbers.
The video introduces the concept of higher-order polynomial equations, which are more challenging than quadratic equations.
The Fundamental Theorem of Algebra is mentioned, stating that the degree of a polynomial equation determines the number of its solutions.
The video discusses the importance of understanding different types of equations, such as linear, quadratic, radical, rational, and exponential equations.
A detailed explanation of what a polynomial is, including its components of coefficients and powers, is provided.
The video emphasizes the necessity of mastering factoring skills for solving polynomial equations.
A method called factoring by substitution is introduced to solve the given polynomial equation.
The process of solving the equation using substitution and factoring is demonstrated step by step.
The video addresses the importance of understanding complex numbers when dealing with higher-order polynomials.
The presenter shares his experience as a math teacher and his passion for making math learning as easy as possible.
The video encourages viewers to subscribe to the channel and utilize the provided resources for learning math concepts.
The presenter offers advice for students struggling with math, emphasizing the need to strengthen foundational skills and understand instruction.
The video concludes with a call to action for viewers to engage with the content, subscribe, and apply the learned math skills.
Transcripts
Browse More Related Video
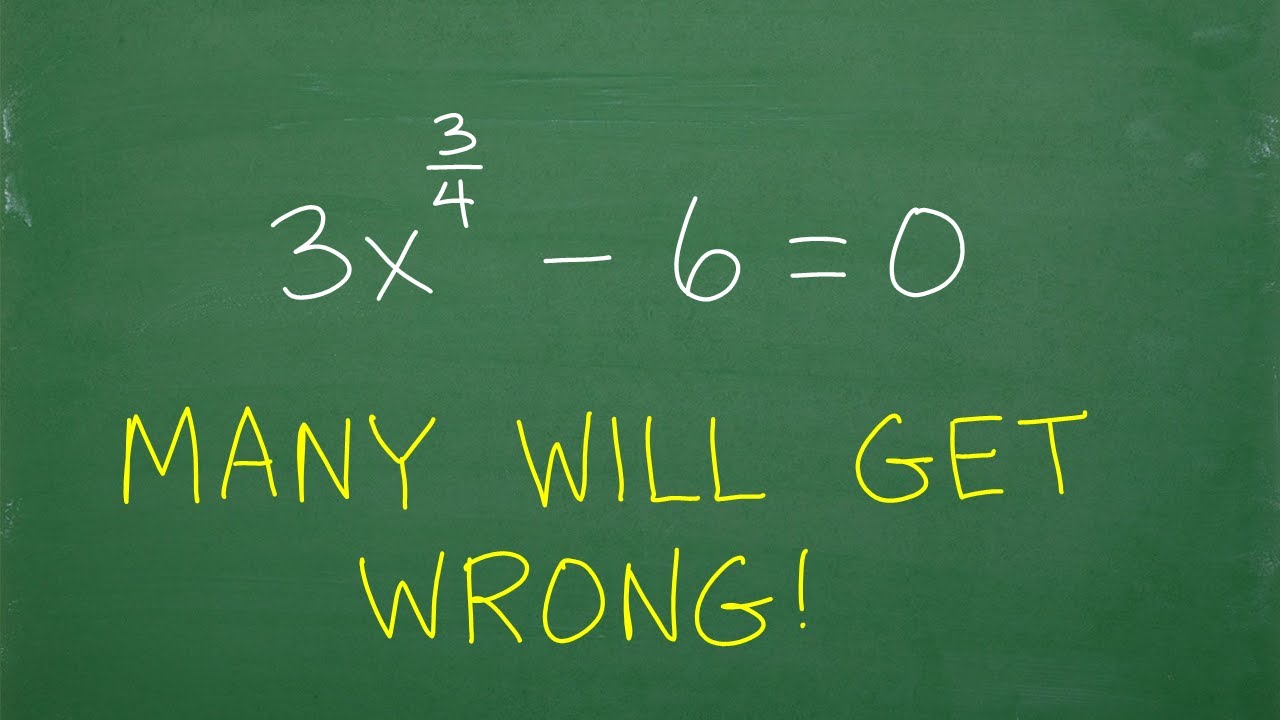
3x to the (3/4) power – 6 = 0, Many don’t know where to start…

NOT EASY to Solve this polynomial equation - USE This! (Rational Root Theorem)

Quadratic Formula – MOST COMMON MISTAKES!
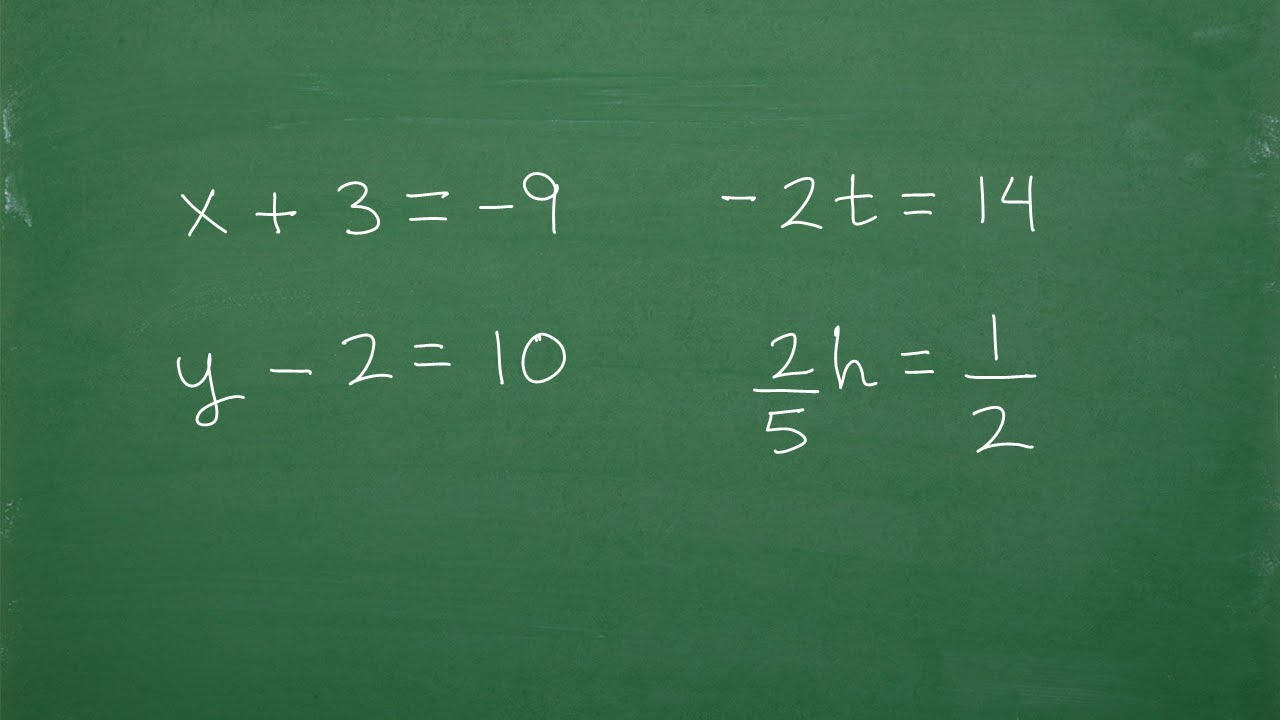
Let’s Solve These Basic Algebra Equations- Step-by-Step…….

The Algebra Step that EVERYONE Gets WRONG!
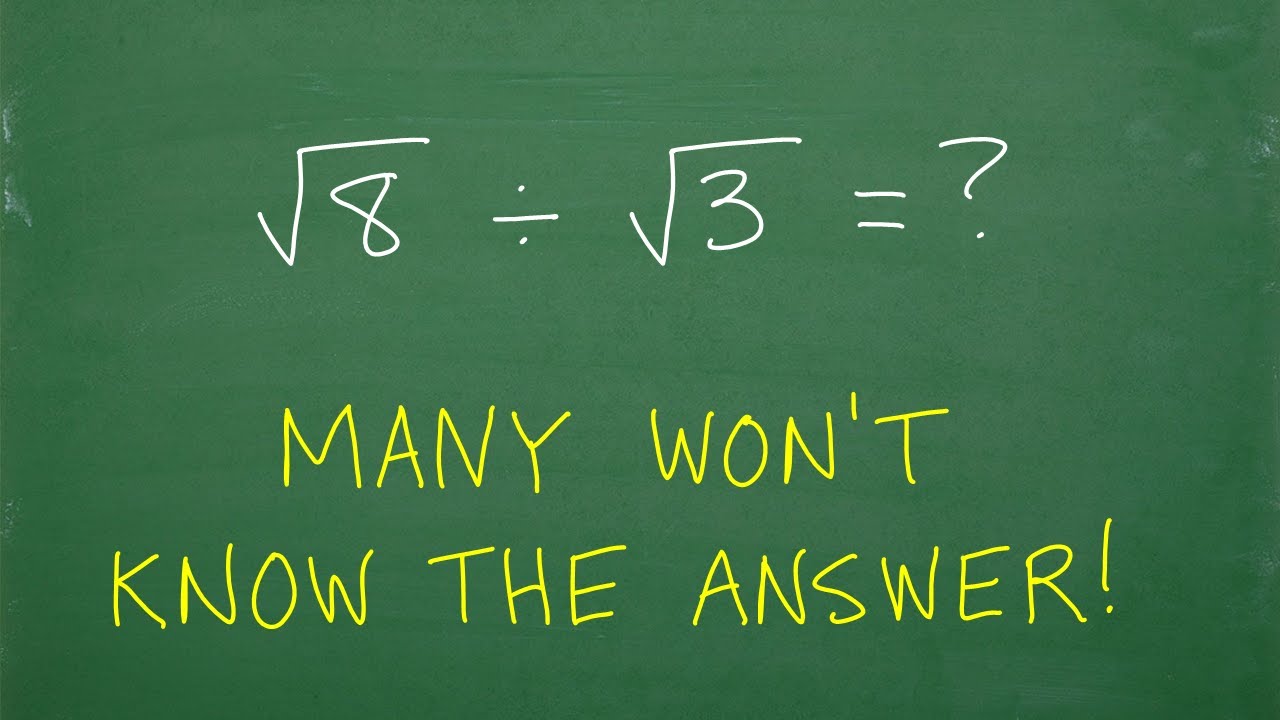
The square root of 8 divided by the square root of 3 =? Many won’t know the ANSWER!
5.0 / 5 (0 votes)
Thanks for rating: