Learn The Quadratic Formula in 10 min

TabletClass Math
12 Jun 201819:55
EducationalLearning
32 Likes 10 Comments

TLDRThis video tutorial offers a concise explanation of the quadratic formula, a fundamental tool in algebra for solving quadratic equations. The presenter provides context, emphasizing its importance in algebra and pre-algebra, and then demonstrates the formula's application with a sample polynomial equation. The focus is on correctly identifying coefficients and carefully plugging them into the formula, highlighting common mistakes students make. The step-by-step process is designed to help viewers master the quadratic formula and understand the concept of two solutions for every quadratic equation.

Takeaways
  • 📚 The video aims to teach the quadratic formula within ten minutes, emphasizing its importance in Algebra One.
  • 🔍 The quadratic formula is specifically for solving quadratic equations, which are second-degree polynomials.
  • 📐 Before applying the quadratic formula, it's recommended to attempt factoring the polynomial equation, if possible.
  • 🔑 The quadratic formula is used when polynomials cannot be factored and is essential for finding the two solutions of a quadratic equation.
  • 📉 The script introduces the concept of 'zeros' and 'roots' as interchangeable terms for the solutions to a quadratic equation.
  • 📈 Understanding the general form of a polynomial and the characteristics of quadratic equations is crucial for applying the quadratic formula correctly.
  • 📝 The standard form of a quadratic equation is required before using the quadratic formula, which is written from the highest to the lowest power.
  • 🔢 The coefficients of the quadratic equation are labeled as 'a', 'b', and 'c', and must be correctly identified and plugged into the formula.
  • 🚫 Common mistakes made by students include incorrect plugging in of values, confusion with negative signs, and errors in calculating the 'b squared minus 4ac' part.
  • 🔄 The 'plus or minus' in the quadratic formula indicates that there are always two solutions to a quadratic equation, which should be calculated separately.
  • 📉 The script provides a step-by-step guide to applying the quadratic formula, highlighting the importance of checking each step for accuracy.
  • 🔍 The video concludes with a reminder of the importance of understanding the quadratic formula and its application in solving quadratic equations.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is to understand and apply the quadratic formula in the context of algebra.

  • Why is the quadratic formula considered critical to know in algebra?

    -The quadratic formula is critical in algebra because it is essential for solving quadratic equations, which are second-degree polynomial equations.

  • What is a quadratic equation?

    -A quadratic equation is a polynomial equation with the highest power of the variable being two, making it a second-degree polynomial.

  • What is the standard form of a quadratic equation?

    -The standard form of a quadratic equation is when it is arranged from the highest power to the lowest power, typically written as ax^2 + bx + c = 0.

  • Why is it important to write the quadratic equation in standard form before applying the quadratic formula?

    -Writing the quadratic equation in standard form ensures that the equation is properly set up for the application of the quadratic formula, with the highest power term first, followed by the linear term and constant term.

  • What are the common mistakes students make when applying the quadratic formula?

    -Common mistakes include plugging in the wrong values for a, b, and c, confusing the signs, especially with negative numbers, and making errors with the b^2 - 4ac part of the formula.

  • What does the plus or minus (±) in the quadratic formula signify?

    -The plus or minus in the quadratic formula signifies that there will always be two solutions to a quadratic equation, one being the positive root and the other being the negative root.

  • Why is it necessary to double-check the values plugged into the quadratic formula before proceeding with calculations?

    -Double-checking ensures accuracy and helps prevent errors that could lead to incorrect solutions. It's crucial to confirm that the correct values for a, b, and c have been substituted into the formula.

  • What is the significance of the term 'b^2 - 4ac' in the quadratic formula?

    -The term 'b^2 - 4ac' is significant as it represents the discriminant of the quadratic equation, which determines the nature of the roots (real and distinct, real and equal, or complex).

  • How does the video script suggest handling the 'b^2 - 4ac' part to avoid common mistakes?

    -The script suggests turning the 'b^2 - 4ac' into 'b^2 + (-4ac)' to avoid confusion with signs, making it clear that it's a sum of b squared and negative four times the product of a and c.

  • What is the final outcome of applying the quadratic formula to a quadratic equation?

    -The final outcome is two solutions for the variable x, which are derived from the plus and minus parts of the quadratic formula, representing the two roots of the equation.

Outlines
00:00
📘 Introduction to the Quadratic Formula

This paragraph sets the context for the video, which aims to explain the quadratic formula within ten minutes. It highlights the importance of the quadratic formula in Algebra 1, mentioning that it's a critical tool for solving quadratic equations, particularly those that can't be factored. The paragraph also introduces the concept of polynomials and their characteristics, specifically focusing on second-degree polynomials, also known as quadratic equations.

05:02
🧮 Identifying Coefficients in a Quadratic Equation

This paragraph explains how to identify the coefficients in a quadratic equation written in standard form (ax² + bx + c = 0). It details the process of assigning the values of a, b, and c based on the given quadratic equation x² - 2x - 15 = 0. The paragraph also emphasizes the importance of correctly identifying and using these coefficients in the quadratic formula to avoid common mistakes.

10:02
🔍 Plugging Values into the Quadratic Formula

Here, the video script details the process of substituting the coefficients into the quadratic formula x = [-b ± √(b² - 4ac)] / 2a. It stresses the importance of using parentheses when substituting negative values to avoid errors. The paragraph also mentions common mistakes students make, particularly with the signs of the coefficients, and advises double-checking the values before simplifying.

15:03
➗ Simplifying the Quadratic Formula

This paragraph guides viewers through the steps of simplifying the quadratic formula after substituting the values. It emphasizes the importance of following the order of operations and working step-by-step to avoid mistakes. The script explains how to handle the square root and the plus/minus sign, which gives the two solutions to the quadratic equation. The paragraph concludes by solving the example quadratic equation, demonstrating how to arrive at the two solutions, x = 5 and x = -3.

🏁 Conclusion and Key Takeaways

In the final paragraph, the video script reviews the entire process of solving a quadratic equation using the quadratic formula. It reiterates the importance of correctly identifying and substituting coefficients, avoiding common mistakes, and understanding the theory behind quadratic equations. The paragraph encourages viewers to practice more problems to master the quadratic formula and hints at more advanced topics related to polynomials and quadratic equations available on the channel.

Mindmap
Keywords
💡Quadratic Formula
The quadratic formula is a fundamental algebraic tool used to solve quadratic equations, which are polynomial equations of the second degree. It is represented as x = ( -b ± sqrt(b^2 - 4ac) ) / 2a . In the video, the formula is the central theme, with the script focusing on how to apply it correctly to find the solutions to a given quadratic equation.
💡Algebra
Algebra is a branch of mathematics that deals with symbols and the rules for manipulating those symbols. It is often introduced to students in middle school and is foundational for higher-level mathematics. In the context of the video, algebra is the subject where the quadratic formula is studied, and it is essential for understanding how to solve quadratic equations.
💡Polynomial Equation
A polynomial equation is an equation in which the variable appears to a power, and the highest power in the equation determines its degree. In the script, the focus is on second-degree polynomial equations, also known as quadratic equations, which the quadratic formula is specifically designed to solve.
💡Factoring
Factoring is a method of solving polynomial equations by breaking them down into simpler components, or factors, that when multiplied together give the original polynomial. The script mentions factoring as the first approach to solving a polynomial equation, before introducing the quadratic formula for cases where factoring is not possible.
💡Quadratic
Quadratic refers to a term, equation, or expression that involves variables raised to the second power. In the video, the term is used to describe a specific type of polynomial equation that the quadratic formula is designed to solve, as indicated by the highest power of the variable being squared.
💡Standard Form
Standard form in the context of polynomial equations is the arrangement of terms from the highest degree to the lowest, typically set equal to zero. The script emphasizes the importance of writing the quadratic equation in standard form before applying the quadratic formula to ensure correct application.
💡Coefficients
In a polynomial equation, coefficients are the numerical factors that multiply the variables. In the script, the coefficients a, b, and c are identified as part of the quadratic equation ax^2 + bx + c = 0 , and they are crucial for correctly applying the quadratic formula.
💡Solutions
Solutions, also referred to as zeros or roots in the script, are the values of the variable that make the equation true, i.e., the values that result in the equation equaling zero. The quadratic formula is used to find these solutions for quadratic equations, and the script explains that there are always two solutions.
💡Plus or Minus
The 'plus or minus' aspect of the quadratic formula indicates that there are two potential solutions to consider, one by adding and one by subtracting the value under the square root. The script explains that this is how the formula yields two solutions, which is a key concept in understanding the nature of quadratic equations.
💡Order of Operations
The order of operations, often remembered by the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction), is a set of rules for performing calculations in a correct sequence. In the script, the order of operations is essential when simplifying the quadratic formula to find the solutions.
Highlights

The video aims to teach the quadratic formula within ten minutes, emphasizing its importance in Algebra One.

Quadratic formula is essential for solving quadratic equations, which are second-degree polynomials.

The presenter introduces an example polynomial equation and explains the characteristics of quadratic polynomials.

Factoring is the first approach to solving a polynomial equation, but not all can be factored, hence the need for the quadratic formula.

The theory of polynomials states that the number of solutions is equal to the highest power of the polynomial.

Quadratic equations have two solutions, referred to as zeros, roots, or solutions.

Understanding polynomials is crucial for successfully applying the quadratic formula.

The quadratic formula should only be used for quadratic equations written in standard form.

Identifying coefficients a, b, and c from the standard form equation is necessary before applying the quadratic formula.

Common mistakes made by students when plugging values into the quadratic formula are highlighted.

The importance of using parentheses and double-checking values before simplifying is emphasized.

The presenter provides a step-by-step guide on correctly applying the quadratic formula.

Students often confuse the signs in the 'b squared minus 4ac' part of the formula, leading to errors.

A technique for avoiding sign confusion is suggested, such as rewriting the expression with a plus-negative sign.

The 'plus or minus' in the quadratic formula is key to obtaining the two separate solutions.

The video concludes with a review of the process and a reminder that the quadratic formula always yields two solutions.

The presenter encourages viewers to subscribe for more content on quadratic equations and polynomials.

The video aims to make viewers proficient with the quadratic formula through a detailed and careful explanation.

Transcripts

Browse More Related Video

Quadratic Formula – MOST COMMON MISTAKES!

Solving Quadratics by Using the Quadratic Formula

Proving the Quadratic Formula - Twice (Precalculus - College Algebra 20)

How To Find The Real & Imaginary Solutions of Polynomial Equations

How to solve a quadratic equation with Casio fx-991MS edition 2 scientific calculator

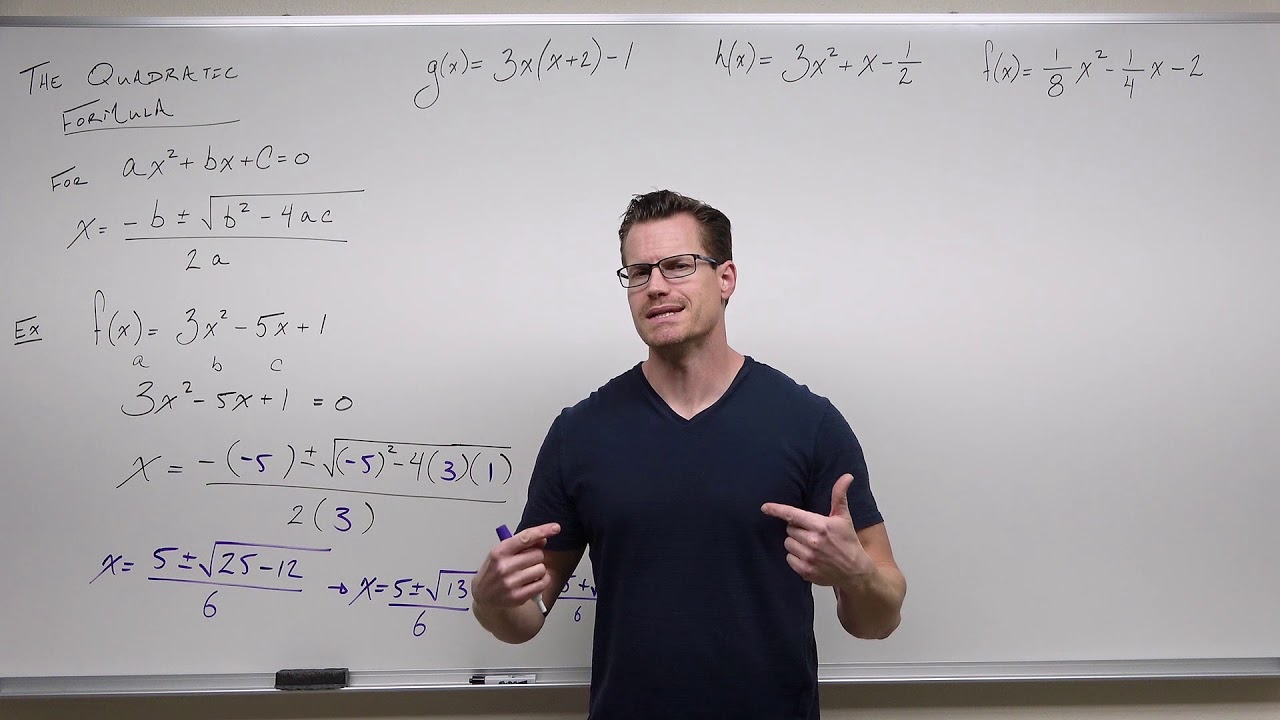
Using the Quadratic Formula (Precalculus - College Algebra 21)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Quadratic FormulaAlgebra OnePolynomial EquationMath EducationFactoring TechniqueRoots and ZerosMathematics TutorialSolving EquationsAlgebraic TechniquesEducational Content