Gravity, Universal Gravitation Constant - Gravitational Force Between Earth, Moon & Sun, Physics
TLDRThe transcript details the calculations of gravitational forces between various objects, such as people, the Earth, and celestial bodies like the Moon and the Sun. It explains how to use the universal law of gravitation, which states that the force is proportional to the product of the masses and inversely proportional to the square of the distance between them. The calculations involve converting units, applying the gravitational constant, and using equations to find the net force in different scenarios, including during a solar eclipse.
Takeaways
- 📝 The force of gravity between two objects can be calculated using the equation F = G * (m1 * m2) / r^2, where G is the gravitational constant, m1 and m2 are the masses of the objects, and r is the distance between them.
- 👥 The gravitational force between a 60 kg person and an 80 kg person 50 cm apart is approximately 1.28 × 10^-6 newtons.
- 🌍 The force of gravity on a 25 kg block on Earth is equivalent to its weight, calculated as mass times the acceleration due to gravity (9.8 m/s^2), resulting in approximately 245 newtons.
- 🌞 The gravitational force exerted by the Sun on the Earth is 3.5 × 10^22 newtons, which is also the force exerted by the Earth on the Sun due to Newton's third law.
- 🌌 To find the distance between two planets, rearrange the gravitational force equation to solve for r, the distance, using the known masses and gravitational force.
- 🚀 The distance between two planets is calculated to be about 5 billion meters using the provided masses and gravitational force.
- 🌕 During a solar eclipse, the Sun's gravitational force on the Moon is greater than the Earth's by approximately 2.398 × 10^20 newtons, pulling the Moon more towards the Sun.
- 🌟 When the gravitational forces from the Earth and the Sun on the Moon are at right angles, the net force on the Moon is calculated using the Pythagorean theorem, resulting in a net force of 4.812 × 10^20 newtons.
- 🔢 Gravitational force calculations are essential for understanding the dynamics of celestial bodies and their interactions.
- 🌌 The gravitational constant (G) is 6.67 × 10^-11 N(m/kg)^2 and is a fundamental constant in physics.
- 📐 Units are crucial in physics problems; ensure that all measurements are converted to the appropriate units (e.g., meters for distance) before performing calculations.
Q & A
What is the formula to calculate the gravitational force between two objects?
-The gravitational force (F) between two objects can be calculated using the formula F = G * (m1 * m2) / r^2, where G is the gravitational constant (6.67 × 10^-11 N(m/kg)^2), m1 and m2 are the masses of the objects, and r is the distance between their centers.
How does the gravitational force between two people with masses of 60 kg and 80 kg, separated by 50 cm, calculate out?
-Using the formula F = G * (m1 * m2) / r^2, and substituting the given values (m1 = 60 kg, m2 = 80 kg, r = 0.5 m), the gravitational force between the two people is approximately 1.28 × 10^-6 N (newtons).
What is the gravitational force exerted on a 25 kg block resting on Earth?
-The gravitational force on the block is equal to its weight, which can be calculated as W = m * g, where m is the mass (25 kg) and g is the acceleration due to gravity on Earth (approximately 9.8 m/s^2). Thus, the force is W = 25 kg * 9.8 m/s^2 ≈ 245 N.
How can you find the distance between two planets if you know the gravitational force between them and their masses?
-You can rearrange the gravitational force formula to solve for distance (r): r = √(G * (m1 * m2) / F), where G is the gravitational constant, m1 and m2 are the masses of the planets, and F is the gravitational force between them.
What is the net force on the Moon when it is between the Earth and the Sun during a solar eclipse?
-The net force on the Moon during a solar eclipse is the difference between the Sun's gravitational force on the Moon (Fs) and the Earth's gravitational force on the Moon (Fe). Since the Sun's mass is much greater than the Earth's, Fs is greater than Fe, resulting in a net force that pulls the Moon towards the Sun.
How does the net force on the Moon change when the gravitational forces from the Earth and the Sun act at right angles to each other?
-The net force on the Moon when the forces are perpendicular can be found using vector addition. It is the hypotenuse of the right triangle formed by the individual forces (Fe and Fs). The net force is calculated as F_net = √(Fs^2 + Fe^2), which results in approximately 4.812 × 10^20 N.
What is the significance of the universal gravitational constant (G) in the force calculation?
-The universal gravitational constant (G) is a key factor in calculating the gravitational force between two objects. It ensures that the force is proportional to the product of the masses and inversely proportional to the square of the distance between them.
How does the mass of the Sun affect the gravitational force it exerts on the Earth?
-The mass of the Sun significantly affects the gravitational force it exerts on the Earth because it is much larger than the mass of the Earth. This large mass results in a strong gravitational pull, which is essential for maintaining the Earth's orbit around the Sun.
What is the role of distance in determining the strength of the gravitational force?
-The distance between two objects plays a crucial role in determining the strength of the gravitational force. The force is inversely proportional to the square of the distance, meaning that as the distance increases, the force decreases rapidly.
How does the gravitational force between two objects compare to the weight of an object on Earth?
-The gravitational force between two objects is calculated using the universal gravitational constant and the masses of the objects divided by the square of the distance between them. In contrast, the weight of an object on Earth is simply the product of its mass and the acceleration due to gravity on Earth (approximately 9.8 m/s^2).
What would be the effect on the gravitational force if the distance between the Earth and the Moon was halved?
-If the distance between the Earth and the Moon was halved, the gravitational force would increase by four times, because the force is inversely proportional to the square of the distance. Halving the distance (2/1 = 2) would result in the force increasing by 2^2 = 4 times.
How does the gravitational force between two planets depend on their masses?
-The gravitational force between two planets is directly proportional to the product of their masses. If one planet's mass is tripled and the other's mass is increased by a factor of 1.5, the gravitational force between them would increase by a factor of 3 * 1.5 = 4.5 times.
Outlines
📚 Calculating Gravitational Force
This paragraph discusses the calculation of gravitational force between two objects. It begins with an example of finding the force of gravity between a 60 kg and an 80 kg person separated by 50 cm. The universal law of gravitation is used, which is represented by the equation F = G * (m1 * m2) / r^2, where G is the gravitational constant, m1 and m2 are the masses of the objects, and r is the distance between them. The calculation involves converting centimeters to meters and squaring the distance. The result is a very small force of 1.2 to 1.28 x 10^-6 newtons. The paragraph then moves on to calculate the gravitational force exerted by the Earth on a 25 kg block, using the Earth's radius and mass, resulting in a force of 244.6 newtons. The concept that weight is the gravitational force on an object is also highlighted, calculated as mass times gravitational acceleration (9.8 m/s^2 on Earth), yielding a similar result to the gravitational force calculation.
🌞 Gravitational Force Between Celestial Bodies
This section focuses on the gravitational force between celestial bodies, specifically the Earth and the Sun. The calculation involves the masses of the Sun and the Earth, as well as the distance between their centers. Using the same gravitational constant G and plugging in the given values, the gravitational force exerted by the Sun on the Earth is calculated to be 3.5 x 10^22 newtons, which is also the force exerted by the Earth on the Sun due to Newton's third law. The problem then extends to finding the distance between two hypothetical planets, X and Y, given their masses and the gravitational force between them. By rearranging the gravitational equation and solving for the distance, the result is approximately five billion meters.
🌕 Net Force on the Moon During Solar Eclipse
This paragraph examines the net force exerted on the Moon when it is positioned between the Earth and the Sun during a solar eclipse. The gravitational forces exerted by both the Sun and the Earth on the Moon are calculated individually, with the Sun's force being greater due to its larger mass. The net force is then determined by subtracting the Earth's gravitational force from the Sun's, resulting in a negative value indicating the direction of the net force towards the Sun. The Moon is pulled more towards the Sun than the Earth in this scenario because of the Sun's significantly larger mass, despite the shorter distance between the Earth and the Moon.
🌟 Net Force on the Moon with Perpendicular Gravitational Forces
The final paragraph explores the net force on the Moon when the gravitational forces from the Earth and the Sun act at right angles to each other. A visual representation is used to illustrate the scenario, with the Sun's gravitational force being greater than the Earth's. The net force is calculated using the Pythagorean theorem, as the forces form the sides of a right-angled triangle. By squaring the individual forces and adding them together, then taking the square root of the sum, the net force acting on the Moon is found to be 4.812 x 10^20 newtons. This calculation demonstrates the combined effect of the gravitational forces from both the Earth and the Sun on the Moon's motion.
Mindmap
Keywords
💡Gravity
💡Universal Gravitation Constant (g)
💡Mass
💡Distance
💡Newton
💡Gravitational Force
💡Earth
💡Sun
💡Moon
💡Celestial Bodies
💡Net Force
Highlights
Calculating the gravitational force between a 60 kg person and an 80 kg person 50 cm apart.
Using the gravitational force equation: g * (m1 * m2) / r^2.
Converting 50 cm to meters for distance calculation.
The universal gravitational constant (g) is 6.67 * 10^-11 N(m^2/kg^2).
Resulting gravitational force between two individuals is 1.28 * 10^-6 N.
Calculating the gravitational force on a 25 kg block resting on Earth.
Using Earth's radius and mass in the gravitational force equation.
The gravitational force on the block is 244.6 N.
Explaining the weight force as mass times gravitational acceleration.
Calculating the force of gravity the Earth experiences from the Sun.
Using the known distance between the Earth and the Sun in the calculation.
Resulting gravitational force of 3.5 * 10^22 N between the Earth and the Sun.
Solving for the distance between two planets given their masses and the force between them.
Finding the distance to be approximately 5 billion meters.
Calculating the net force on the Moon when it's between the Earth and the Sun.
The Sun's gravitational force on the Moon is greater than the Earth's during a solar eclipse.
The net force on the Moon is directed towards the Sun due to the Sun's greater mass.
Determining the net force on the Moon when Earth and Sun's gravitational forces are at right angles.
The net force on the Moon in this position is 4.812 * 10^20 N.
Transcripts
Browse More Related Video

Gravitation Class 9 Science | CBSE | NCERT | Universal law of Gravitation

Understanding Universal law of Gravitation!
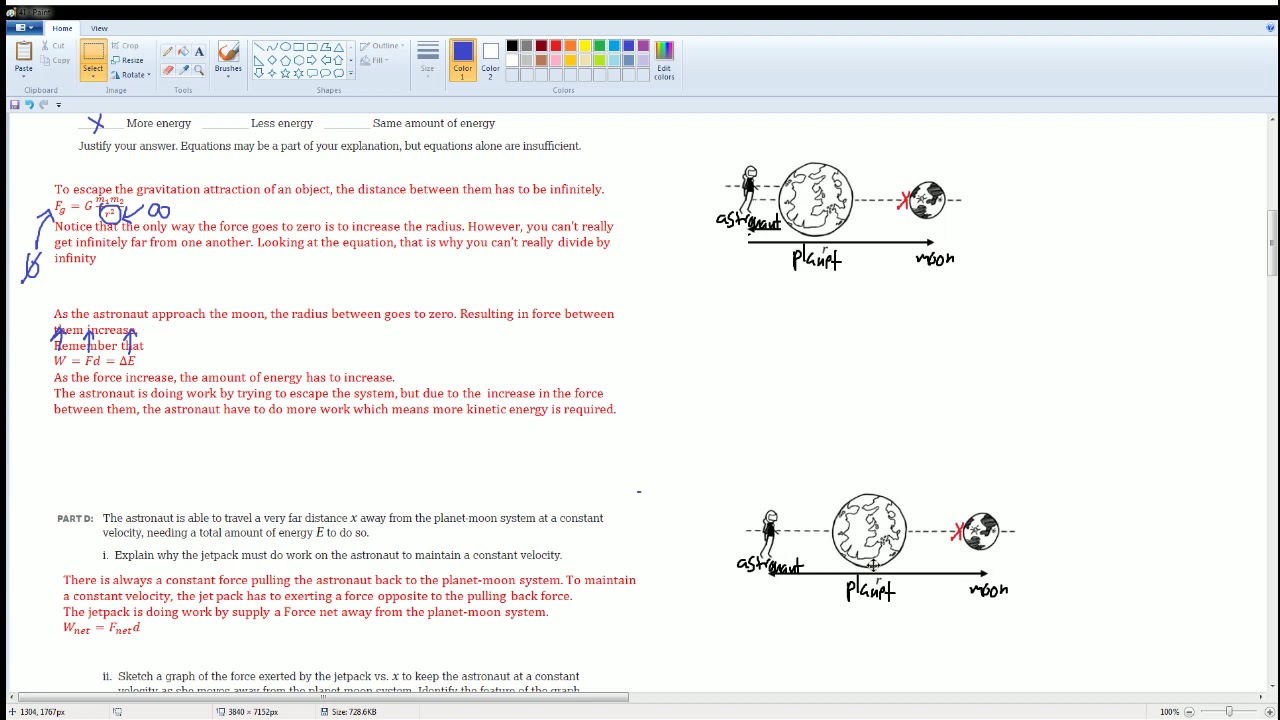
AP Physics Workbook 4.I Gravitational Potential Energy
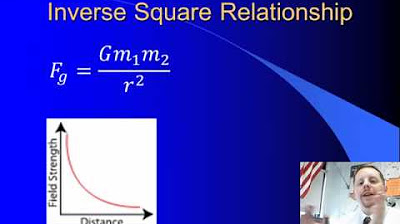
High School Physics - Newton's Law of Universal Gravitation

Newton's Law of Universal Gravitation
Centripetal Acceleration & Force - Circular Motion, Banked Curves, Static Friction, Physics Problems
5.0 / 5 (0 votes)
Thanks for rating: