Newton's 2nd Law of Motion in Physics Explained - [1-5-6]
TLDRIn this lesson, the importance of Newton's second law of motion is emphasized, highlighting its fundamental role in understanding how forces influence motion. The law, expressed as F=ma, is explained in detail, including its vector nature and the relationship between force, mass, and acceleration. Practical insights are provided, such as the conversion factor role of mass and the concept of net force when multiple forces are involved. The lesson also demonstrates how to apply the law to calculate acceleration and displacement, using a space probe example to illustrate the concepts.
Takeaways
- 📚 Newton's Second Law of Motion is fundamental in physics, essential for understanding motion, friction, and forces in space and electromagnetism.
- 🚀 The law states that the force applied to an object is equal to the mass of the object multiplied by its acceleration (F = ma), and highlights the relationship between force, mass, and acceleration.
- 🔢 The units for force are Newtons (N), for mass are kilograms (kg), and for acceleration are meters per second squared (m/s²).
- 🧭 Newton's Second Law helps in calculating the force needed to achieve a certain acceleration when the mass of an object is known, and vice versa.
- 🔄 Forces cause changes in motion, not motion itself. Objects move in a straight line without forces, but forces cause acceleration, which changes the state of motion.
- 🎯 The direction of the force and the acceleration must be the same, as they are vector quantities, and the mass acts as a conversion factor between force and acceleration.
- 📐 Newton's Second Law can be applied to both individual forces and the net force acting on an object, where multiple forces are vectorially summed up to find the resultant force.
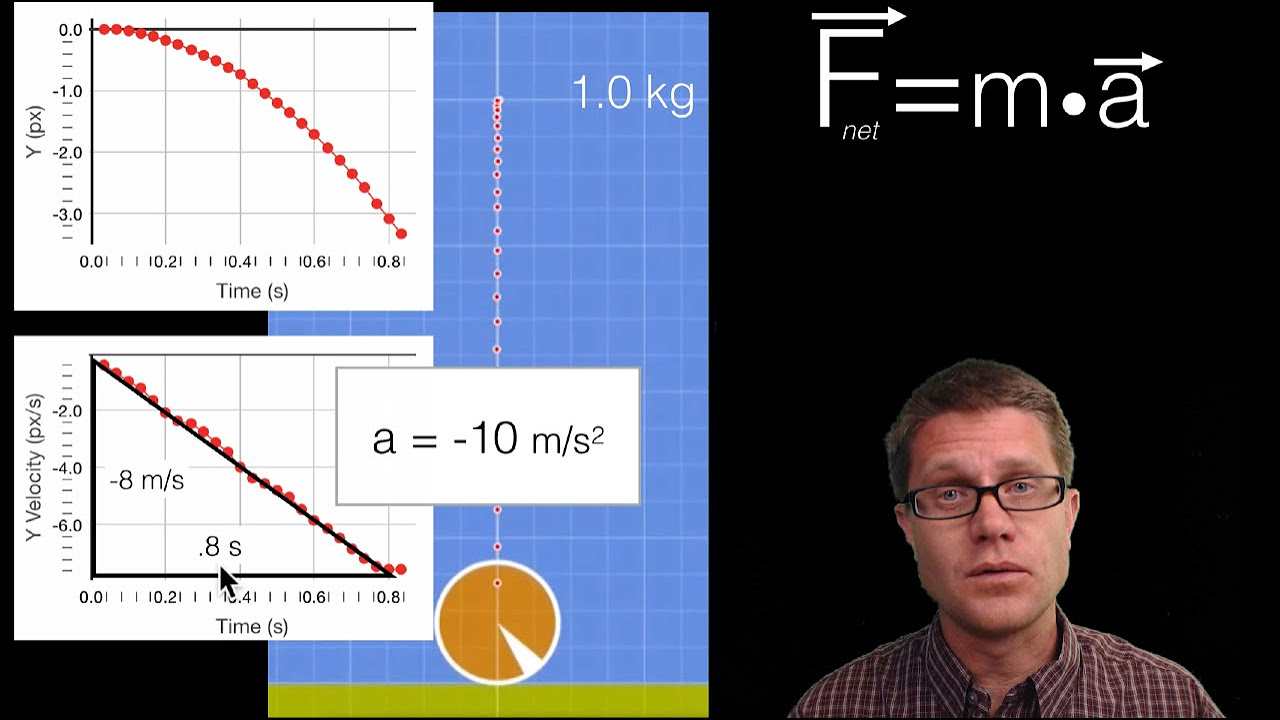
- 🚀📈 The law can be graphically represented to show how force, mass, and acceleration interact over time, resulting in changes in velocity and position.
- 🌌 The concept of inertia is related to mass; more massive objects resist changes in motion more than lighter ones when the same force is applied.
- 📝 Example problem-solving using the law involves calculating the acceleration of a space probe due to a tractor beam force and determining the distance traveled by the probe over a given time.
- 🔍 Understanding Newton's Second Law is crucial for grasping a wide range of physical phenomena and is applicable across various fields of physics.
Q & A
What is the main focus of this lesson?
-The main focus of this lesson is Newton's second law of motion, which states that the force applied to an object is equal to the mass of the object multiplied by its acceleration (F = ma).
Why is Newton's second law of motion considered essential in physics?
-Newton's second law of motion is considered essential because it is fundamental to understanding how forces influence the motion of objects, including frictional forces, motion through space, spacecraft, and even electromagnetic forces.
How does Newton's first law relate to the second law?
-Newton's first law states that an object at rest stays at rest and an object in motion stays in motion with a constant velocity unless acted upon by an external force. The second law builds upon this by explaining that forces cause changes in motion, or accelerations.
What are the units for force, mass, and acceleration in the context of Newton's second law?
-The force is measured in Newtons (N), the mass is measured in kilograms (kg), and the acceleration is measured in meters per second squared (m/s^2).
What does the vector nature of force and acceleration in Newton's second law imply?
-The vector nature implies that force and acceleration both have magnitude and direction, and they must be aligned in the same direction for the equation F = ma to hold true.
How does the mass of an object act in the equation F = ma?
-The mass of an object acts as a conversion factor between force and acceleration. It determines how much acceleration is produced by a given force.
What is the significance of the net force in the context of multiple forces acting on an object?
-The net force is the vector sum of all the individual forces acting on an object. It represents the single force that is equivalent to the combined effect of all the individual forces and is what actually causes the acceleration of the object.
How does the problem of a space probe being subjected to a tractor beam illustrate Newton's second law?
-The problem illustrates that the constant force from the tractor beam (140 N) applied to the space probe (32.50 kg) results in an acceleration (4.31 m/s^2), which can then be used to calculate the distance the probe moves in 10 seconds (215.5 meters).
What is the definition of a Newton?
-A Newton is the amount of force required to accelerate a one-kilogram mass by one meter per second squared.
How does the direction of force affect the velocity of an object?
-If the force is applied in the same direction as the velocity, the object speeds up. If the force is applied in the opposite direction, the object slows down. The force and acceleration always align in direction, but the velocity and acceleration do not necessarily have to align.
What is the relationship between the force applied and the resulting motion of an object?
-The force applied to an object (measured in Newtons) is directly related to the acceleration produced (measured in m/s^2) through the mass of the object (measured in kg). This relationship is fundamental for calculating changes in motion and predicting the behavior of objects under various forces.
Outlines
📚 Introduction to Newton's Second Law of Motion
The video begins with an introduction to Newton's second law of motion, emphasizing its fundamental importance in physics. It mentions a common saying about the law's applicability to solving almost any physics problem. The lesson aims to provide a deep understanding of the law, moving beyond standard textbook explanations. It revisits Newton's first law, which states that forces do not cause motion but rather cause changes in motion, specifically acceleration. The video sets the stage for a detailed exploration of how forces influence motion, particularly in the context of acceleration.
📈 Newton's Second Law: Force as a Vector
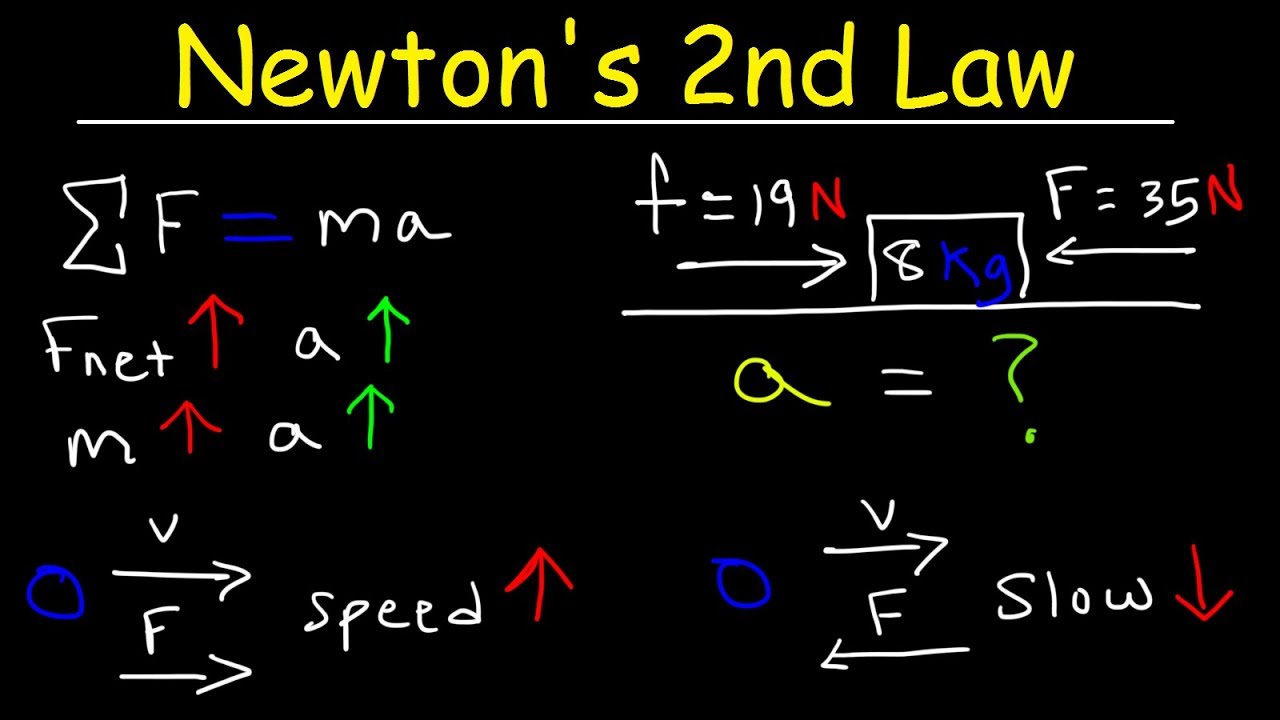
This paragraph delves into the mathematical expression of Newton's second law, which states that the force applied to an object is equal to the mass of the object multiplied by its acceleration (F=ma). It highlights that force and acceleration are vector quantities, meaning they have both magnitude and direction. The explanation includes a discussion on the units of measurement for force (Newtons), mass (kilograms), and acceleration (meters per second squared). The video also emphasizes the importance of direction in vector equations and provides examples of how forces and accelerations align in different scenarios, including when forces are applied at an angle.
🔄 Decomposition of Forces and Acceleration
The video continues by explaining how to decompose forces and acceleration into their component parts along the X and Y axes. It illustrates how a force applied in a specific direction results in an acceleration in the same direction. The concept of net force is introduced, explaining that the combined effect of multiple forces on an object can be represented as a single force, the net force. This net force is then related to the mass and acceleration of the object through Newton's second law. The video uses visual examples to demonstrate how forces and accelerations are resolved into components and how they influence the motion of an object.
🌐 Philosophical Insights on Force and Mass
This section offers philosophical insights into the relationship between force, mass, and acceleration. It describes mass as a conversion factor that determines how much influence a force has on producing acceleration. The video likens mass to a conversion factor between units of measurement, such as meters to centimeters. It explains that the force and acceleration are essentially the same thing, differing only in the scale factor provided by the mass. This understanding helps to clarify the role of mass in the equation F=ma and its impact on the motion of objects.
🚀 Graphical Representation of Force and Acceleration
The video provides a graphical representation of how force and acceleration interact over time. It uses the example of a magnet to demonstrate that constant force leads to constant acceleration, resulting in a continuous increase in velocity. The video then contrasts this with a scenario where the force is removed, leading to coasting at a constant velocity. It also explores what happens when a force is applied in the opposite direction to the motion of an object, resulting in deceleration. The graphical examples aim to clarify the relationship between force, acceleration, and velocity, and how they contribute to the overall motion of an object.
📌 Solving a Physics Problem: Space Probe and Newton's Second Law
The video presents a practical problem involving a space probe subjected to a constant force from a ship's tractor beam. It guides the viewer through the process of calculating the probe's acceleration due to the force and then determining the distance the probe moves in 10 seconds. The problem-solving process involves applying Newton's second law to find the acceleration and using the equations of motion to calculate the distance traveled. The video reinforces the concept that force leads to acceleration, which in turn leads to motion, and demonstrates how these principles can be applied to solve real-world physics problems.
🎓 Conclusion and Preview of Future Lessons
The video concludes by reiterating the significance of Newton's second law of motion in understanding the relationship between force and motion. It emphasizes that the law is a vector equation and that the direction of the force and acceleration must align. The video also highlights the importance of understanding the net force when multiple forces are involved. It encourages the viewer to practice the concepts learned and previews future lessons that will further explore problems involving Newton's second law of motion.
Mindmap
Keywords
💡Newton's Second Law of Motion
💡Acceleration
💡Force
💡Mass
💡Vector
💡Tractor Beam
💡Newton
💡Equations of Motion
💡Inertia
💡Space Probe
Highlights
Newton's second law of motion is introduced as one of the most important lessons in physics.
The lesson emphasizes the importance of understanding Newton's second law for solving a wide range of physics problems involving forces.
The fundamental concept that forces cause motion to change, not to initiate motion, is reiterated.
Newton's second law is mathematically expressed as F = ma, where F is the force, m is the mass, and a is the acceleration.
The vector nature of force and acceleration is highlighted, with direction being a crucial component.
The units for force, mass, and acceleration are Newtons, kilograms, and meters per second squared, respectively.
The concept of mass as a conversion factor between force and acceleration is introduced.
The philosophical insight that force and acceleration are related by the mass of the object is discussed.
The net force acting on an object is the vector sum of all individual forces acting on it.
The graphical representation of how force affects velocity and acceleration is provided.
A practical example of a space probe being accelerated by a tractor beam is used to illustrate the application of Newton's second law.
The problem-solving approach involves calculating the acceleration due to a known force and then determining the distance traveled.
The definition of a Newton is explained as the force required to accelerate a one-kilogram mass by one meter per second squared.
The lesson concludes with the application of Newton's second law to solve a problem involving a space probe's acceleration and distance traveled.
The importance of understanding the vector nature of Newton's second law is emphasized for solving physics problems.
The lesson underscores the universal application of Newton's laws across various domains of physics.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: