Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (36 of 92) Finite Potential Well Part 5

Michel van Biezen
26 Mar 201804:38
EducationalLearning
32 Likes 10 Comments

TLDRThis script delves into the behavior of particles within finite wells, contrasting it with those in infinite wells. It explains how the solutions to the SchrΓΆdinger equation differ inside the barriers and in the well, highlighting the presence of decay functions and the role of energy levels. The discussion includes the impact on wavelength and momentum, noting that particles in finite wells have slightly longer wavelengths and lower momenta than those in infinite wells of the same width. The script outlines the conditions for the functions' values and slopes to match at boundaries, leading to specific energy levels and penetration depths within finite wells.

Takeaways
  • 🌟 In a finite well, the solutions to the Schrodinger equation exhibit probability within the barriers, indicating the presence of the particle outside the well's boundaries.
  • πŸ“ˆ The wave functions in regions one and three feature decay functions, while region two (inside the well) has sine and cosine components, depending on the energy level.
  • πŸ”’ Quantum numbers determine the different energy levels (subscripts n, m, etc.) and the corresponding waveforms of the particle within the well.
  • πŸŒ€ As energy increases, the particle exhibits an increasing number of wavelengths, with energy defined by the formula n^2 * Ο€^2 * Hbar^2 / (2m * L^2), where L is the well's length.
  • πŸ”— Boundary conditions require that the function values and their derivatives match at x=0 and x=L, ensuring continuity across the well and barriers.
  • πŸ›‘ The actual wavelength in a finite well is slightly larger than in an infinite well of the same width, affecting the energy levels and momentum.
  • 🌊 For the first energy level, the well length equals half a wavelength, but in a finite well, this half-wavelength is slightly longer than the well's length.
  • πŸš€ The momentum of a particle in a finite well is smaller than in an infinite well at the same energy level due to the longer wavelengths.
  • πŸ“Œ Specific values for energy levels (e_sub_n) and penetration depth can be calculated based on the particle's mass and energy.
  • πŸ“‹ Understanding these constraints allows for the precise definition of wave functions inside and outside the well, and the determination of finite well characteristics.
Q & A

  • What is the main difference in the solutions to the Schrodinger equation for a finite well compared to an infinite well?

    -In a finite well, there is a probability that the particle will be found within the barrier regions, which is not the case in an infinite well where the probability is zero within the barriers.

  • How does the wave function behave in region one and region three of a finite well?

    -In region one and region three, the wave function exhibits a decay function to the left and right, respectively, indicating the probability of the particle's presence in these regions.

  • What are the key components of the wave function in region two of a finite well?

    -In region two, the wave function has both a sine and a cosine component, which are related to the energy levels and the quantum number of the particle.

  • How does the energy of a particle in a finite well relate to the quantum number and the dimensions of the well?

    -The energy of a particle is given by the formula E_n = (n^2 * Ο€^2 * Hbar^2) / (2m * L^2), where n is the quantum number, m is the mass of the particle, L is the length of the well, and Hbar is the reduced Planck constant.

  • What is required for the wave functions to match at the boundary of the well?

    -At the boundary, the value of the function and its slope must be equal on both sides of the boundary. This ensures continuity and physical relevance of the solutions.

  • How does the wavelength of a particle in a finite well compare to that in an infinite well?

    -The actual wavelength in a finite well is slightly larger than it would be in an infinite well of the same width. This is because in a finite well, the particle's wave function extends slightly beyond the boundary.

  • What is the relationship between the wavelength and the momentum of a particle in a finite well?

    -The momentum of a particle is inversely proportional to the wavelength (p = H / Ξ»). Since the wavelength in a finite well is slightly larger than in an infinite well for the same energy level, the momentum in a finite well is slightly smaller.

  • What are the constraints on the energy levels in a finite well?

    -The energy levels in a finite well are quantized and depend on the quantum number, the mass of the particle, and the dimensions of the well. These constraints ensure that only specific values of energy can exist.

  • How does the penetration depth in a finite well depend on the mass and energy of the particle?

    -The penetration depth is influenced by the mass of the particle and its energy level. The specific values for the penetration depth are determined by the solutions to the Schrodinger equation that satisfy the boundary conditions.

  • What is the significance of the boundary conditions in solving the Schrodinger equation for a finite well?

    -The boundary conditions are crucial for finding the exact solutions to the Schrodinger equation. They ensure that the wave functions and their slopes are continuous at the boundaries, which is necessary for physically meaningful solutions.

  • How does the concept of finite and infinite wells relate to the understanding of quantum confinement?

    -Finite and infinite wells are fundamental models in quantum mechanics that help in understanding quantum confinement effects. In a finite well, the confinement leads to quantized energy levels and modified wave functions compared to the infinite well, where the confinement is complete and the energy levels are also quantized but without wave function penetration outside the well.

Outlines
00:00
🌟 Introduction to Finite Wells and Quantum States

This paragraph introduces the concept of finite quantum wells and their implications on particle behavior. It explains the difference in the SchrΓΆdinger equation solutions within the barriers of finite wells, highlighting the probability of particle existence in these regions. The discussion also touches on the decay functions in regions one and three, and the sine and cosine components of the equation in region two, where the particle's energy is above the absolute zero floor level. The role of quantum numbers and energy levels in determining the particle's waveform within the well is emphasized, as well as the relationship between energy, wavelength, and the well's length. The paragraph concludes with the necessity of matching function values and slopes at the boundaries for the equations to align correctly.

Mindmap
Keywords
πŸ’‘Finite Wells
Finite Wells refer to a quantum mechanical model where a particle is confined within a potential well of finite depth and width. Unlike infinite wells, where the potential energy is infinitely high at the boundaries, finite wells allow for the possibility of the particle being found outside the well, albeit with lower probability. This concept is central to the video's discussion on the behavior of particles in quantum mechanics.
πŸ’‘Schrodinger Equation
The Schrodinger Equation is a fundamental equation in quantum mechanics that describes how the quantum state of a physical system changes with time. It is used to calculate the probability distribution of particles in various physical scenarios. In the context of the video, the Schrodinger Equation is used to determine the wave function of a particle within a finite well, which helps in understanding its behavior.
πŸ’‘Probability
In quantum mechanics, probability is used to describe the likelihood of finding a particle in a particular state or position. It is a key concept in understanding the behavior of particles within potential wells, as it relates to the wave function's squared amplitude. The video emphasizes the probability of a particle being present inside and outside the finite well, which is determined by the wave function's solutions.
πŸ’‘Wave Function
A wave function is a mathematical function that describes the quantum state of a particle or system in quantum mechanics. It contains all the information about the system and is used to calculate probabilities of various physical quantities. In the video, the wave functions for different regions within the finite well are discussed, which are essential for understanding the particle's energy levels and behavior.
πŸ’‘Energy Levels
Energy levels in quantum mechanics refer to the discrete amounts of energy that a particle can have within a potential well. These levels are determined by the shape of the potential and are quantized, meaning that a particle can only exist with these specific energy values. The video script discusses how energy levels are quantized and depend on the quantum number, which is related to the wave function's form within the well.
πŸ’‘Quantum Number
A quantum number is an integer that describes the unique quantum states of particles in a quantum system. It is used to characterize the energy levels and wave functions of particles within potential wells. In the context of the video, quantum numbers determine the specific waveform and energy levels of a particle within a finite well, influencing its behavior and properties.
πŸ’‘Boundary Conditions
Boundary conditions in the context of the Schrodinger Equation are the constraints that must be satisfied at the edges of the region being studied. They are essential for solving the equation and finding the wave functions that describe the particle's behavior. In the video, boundary conditions are used to ensure that the wave functions and their slopes are continuous at the boundaries of the finite well.
πŸ’‘Wavelength
In physics, the wavelength is the spatial period of a waveβ€”the distance over which a wave's form repeats. In the context of particles in a finite well, the wavelength is related to the particle's momentum and energy level. The video script notes that the actual wavelength inside a finite well is slightly larger than what would be expected in an infinite well of the same width, affecting the particle's momentum.
πŸ’‘Momentum
Momentum in physics is the product of a particle's mass and its velocity. In quantum mechanics, momentum is related to the wavelength of a particle through the de Broglie hypothesis, which states that the wavelength is inversely proportional to the momentum. The video explains that in a finite well, the momentum of a particle is slightly smaller than in an infinite well due to the longer wavelength.
πŸ’‘Potential Energy
Potential energy is the stored energy an object has due to its position in a force field, such as a gravitational or electric field. In quantum mechanics, potential energy is associated with the energy states of particles within a potential well. The video discusses finite and infinite wells, where the potential energy is zero within the well and increases at the boundaries, affecting the particle's energy levels and behavior.
πŸ’‘Fenestration Depth
Fenestration depth, while not explicitly defined in the script, can be inferred as the depth or extent to which a particle's wave function penetrates the barriers of a finite well. This concept is crucial in understanding the probability distribution of the particle's presence outside the well. The depth of penetration is influenced by the energy levels and the properties of the well.
Highlights

Finite wells and particles exhibit solutions to the Schrodinger equation that differ inside the barriers.

There is a probability for a particle to be found inside the barriers, which will be discussed later.

The solution for region one shows a decay function to the left, and region three shows a decay function to the right.

In region two, where the particle's energy is above the absolute floor zero energy level, the equation includes a sine and cosine portion.

Different energy levels are associated with different wave forms for the particle within the well, determined by quantum numbers.

The energy of the particle is defined as n^2 * Ο€^2 * H_bar^2 / (2m * L^2), with L being the length of the well.

For the equations to match, the function values and slopes at x=0 and x=L must be equal.

The actual wavelength inside a finite well is slightly larger than in an infinite well of the same width.

In a finite well, the particle extends slightly beyond the boundary, requiring a longer wavelength for the functions to align.

The momentum of a particle in a finite well is smaller than in an infinite well for the same energy level due to the longer wavelength.

The specific values for energy levels (e_sub_n) and penetration depth depend on the mass and energy of the particle.

Strict rules can be defined to find the exact equations that match inside and outside the well, and to determine the fenestration depth.

Understanding these constraints is key to working with potential finite wells.

The decay functions in regions one and three are crucial for understanding the behavior of particles within finite wells.

The sine and cosine components in region two are indicative of the particle's wave-like behavior within the well.

Matching function values and slopes at the boundaries is essential for solving the Schrodinger equation for finite wells.

The wavelength and momentum differences between finite and infinite wells of the same width are significant for quantum mechanics.

Transcripts

Browse More Related Video

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (17 of 92) How to Use Schrod. Eqn: 2

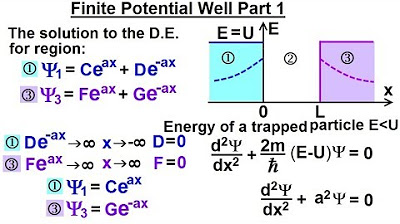
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (32 of 92) Finite Potential Well Part 1

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (18 of 92) Particle in 1-D Box: Gen. Appr.

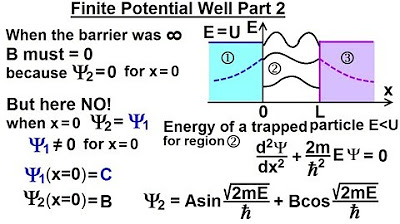
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (33 of 92) Finite Potential Well Part 2

Lecture 11: Dispersion of the Gaussian and the Finite Well

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (61 of 92) Reflection & Transmission

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Quantum MechanicsFinite WellsSchrodinger EquationParticle BehaviorProbability WavesEnergy LevelsWave FunctionsQuantum BarriersWavelength AnalysisMomentum Comparison