Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (1 of 92) The Wave Equation

Michel van Biezen
16 Nov 201607:41
EducationalLearning
32 Likes 10 Comments

TLDRThis video delves into the origins and significance of Schrödinger's equation, the fundamental equation in quantum mechanics that describes the behavior of small particles with wave-like properties. It highlights the challenges in deriving the equation and the process of making analogies between particles and photons. The video also explains the concept of wave functions and probability density functions, which are essential for understanding the probabilistic nature of quantum mechanics. The accuracy of Schrödinger's equation is confirmed through its consistent agreement with experimental data, and the video promises further exploration of the equation and its applications in future installments.

Takeaways
  • 🌟 Schrodinger's equation is used to describe the motion and energy of small particles, which exhibit wave-like properties similar to photons.
  • 🤔 The derivation of Schrodinger's equation was based on assumptions and analogies rather than a direct physical law, due to the lack of a clear derivation method.
  • 🌊 Small particles' behavior is analogous to photons, blurring the line between their particle and wave characteristics.
  • 📈 The equation was developed by drawing parallels between the behavior of particles and the known properties of photons.
  • 🔄 The wave function, central to quantum mechanics, is complex with real and imaginary parts, unlike physical waves which have a direct physical interpretation.
  • 🎲 The probability density function is derived from the wave function by squaring it and removing the imaginary part through complex conjugation.
  • 📊 The probability of finding a particle is represented by the area under the probability density curve, with higher probabilities in regions where the wave function is larger.
  • 🌐 The wave function incorporates position and time through the wave number (k) and angular frequency (ω), represented as 𝑘𝑥 - 𝜔𝑡.
  • 🌈 The wave function can be expanded into sines and cosines, similar to classical wave functions, but with no direct physical meaning until squared for probability.
  • 🧪 Experimental data has largely confirmed the predictions of Schrodinger's equation, providing confidence in its accuracy for describing the motion of small particles.
  • 📚 Further videos will delve into the nuances of Schrodinger's equation, including its application to quantum phenomena like wells and barriers.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is the Schrödinger equation, which describes the motion, energy, and position of small particles with wave-like properties.

  • Why was the Schrödinger equation developed?

    -The Schrödinger equation was developed because small particles, like electrons, exhibit wave-like properties similar to photons, and there was a need for an equation to describe their behavior and reaction to forces.

  • How did Schrödinger approach the creation of his equation?

    -Schrödinger made some assumptions based on the knowledge available at the time, drawing analogies between particles and photons, and developed the equation without a direct derivation method.

  • What is the significance of wave functions in quantum mechanics?

    -Wave functions are crucial in quantum mechanics as they describe the probability density function of finding a particle in a particular location, with the square of the wave function representing this probability.

  • How is the physical meaning derived from a wave function?

    -The physical meaning is derived by squaring the wave function to obtain the probability density function, which removes the imaginary part and leaves a real quantity representing a feature of particles.

  • What does the wave number (K) represent in the context of wave functions?

    -The wave number (K) is equal to 2π over the wavelength (λ) and is a part of the wave function that describes the particle's wave-like properties in terms of position.

  • How does the time dependency get incorporated into the wave function?

    -The time dependency is incorporated by including a term with the angular frequency (Ω) and time (t), often represented as -Ωt, which is combined with the KX term to describe the wave function over time.

  • What is the role of the Hamiltonian in the context of the Schrödinger equation?

    -The Hamiltonian is used to describe the motion and energy of particles in the Schrödinger equation, providing a way to analyze the system's behavior and energy states.

  • How was the correctness of the Schrödinger equation verified?

    -The correctness of the Schrödinger equation was verified by comparing the theoretical predictions with experimental outcomes, which consistently matched, thus confirming the equation's accuracy in describing the motion of small particles.

  • What is the purpose of further analyzing the Schrödinger equation in upcoming videos?

    -The purpose is to provide a deeper understanding of the equation, explore its derivation, and learn how to apply it to various quantum mechanical systems, such as wells and barriers.

  • Why is there a thin line between photons and particles as discussed in the video?

    -The thin line between photons and particles is due to the wave-particle duality concept, where both exhibit properties of waves and particles, making it difficult to distinguish their exact nature based solely on their behavior.

Outlines
00:00
🌪️ Introduction to Schrödinger's Equation and Wave-Particle Duality

This paragraph introduces the concept of Schrödinger's equation, which is used to describe the motion and energy of small particles that exhibit wave-like properties. It explains that particles behave similarly to photons, and there is a fine line between their behaviors. The development of the equation is discussed, highlighting that it was based on assumptions and analogies rather than a direct derivation. The importance of wave functions and probability density functions in representing the likelihood of finding a particle at a particular location is emphasized, as well as the process of squaring the wave function to eliminate imaginary parts and obtain a real quantity.

05:01
📶 Wave Functions and Time Dependency in Quantum Mechanics

The second paragraph delves into the specifics of wave functions in quantum mechanics, including the time dependency of these functions. It explains how the wave function can be represented by a sine or cosine with amplitude and wave number, and how the time factor is incorporated through the term minus Omega T. The paragraph also discusses the verification of Schrödinger's equation through experimental outcomes, which have largely matched the theoretical predictions. This has led to a strong confidence in the equation's ability to accurately describe the motion of small particles. The paragraph concludes by mentioning that future videos will explore the equation further and its applications in various quantum phenomena.

Mindmap
Keywords
💡Schrodinger's Equation
Schrodinger's Equation is a fundamental equation in quantum mechanics that describes how quantum systems evolve over time. It was developed by Erwin Schrodinger and is central to understanding the behavior of particles at a quantum level. In the video, it is mentioned that this equation was derived from assumptions and analogies rather than a direct derivation, as was the case with classical mechanics equations. It is used to calculate the probability of finding a particle in a particular state and is essential for describing the wave-like properties of particles.
💡Wave-like Properties
Wave-like properties refer to the behavior of particles that exhibit characteristics of waves, such as interference and diffraction. In quantum mechanics, particles like electrons display both particle and wave characteristics, which is a concept known as wave-particle duality. The video explains that this dual nature led to the creation of a wave equation to describe the behavior of particles, highlighting the thin line between particles and photons in terms of their wave-like nature.
💡Wave Function
A wave function is a mathematical function used in quantum mechanics to calculate the probability amplitude of a particle's location. It is a complex function with both real and imaginary parts, and its square gives the probability density function. The wave function is essential for understanding the probabilistic nature of quantum mechanics and predicting where particles are likely to be found.
💡Probability Density Function
The probability density function is the square of the wave function, which represents the likelihood of finding a particle in a particular position. It is a real-valued function that integrates to one over all space, ensuring that the total probability of finding the particle somewhere is 100%. This function is crucial for making predictions in quantum mechanics about the distribution of particles.
💡Complex Conjugate
The complex conjugate of a complex number is the number with the same real part but the opposite sign for the imaginary part. In the context of wave functions, multiplying by the complex conjugate eliminates the imaginary part, leaving a real-valued function that can be squared to obtain the probability density function.
💡Wave Number (K)
The wave number, denoted by K, is a measure of the spatial frequency of a wave, defined as the number of radians in one wavelength (2π over the wavelength, λ). It is a key parameter in wave equations and describes how rapidly the wave function oscillates with respect to position.
💡Amplitude
Amplitude in the context of waves refers to the maximum displacement of a point on the wave from its equilibrium position. In the wave function, amplitude is the coefficient that multiplies the sine or cosine function, representing the relative strength or intensity of the wave.
💡Energy and Momentum
In quantum mechanics, energy and momentum are key quantities that describe the state of a particle. Energy is related to the frequency of the wave function, while momentum is related to the wave number. These quantities are essential for understanding the behavior of particles, especially in the context of quantum mechanics where particles exhibit wave-particle duality.
💡Quantization
Quantization is the process of restricting physical quantities to discrete values, which is a fundamental concept in quantum mechanics. It implies that properties like energy, momentum, and angular momentum can only take on certain discrete values rather than any continuous range.
💡Hamiltonian
The Hamiltonian is a function used in classical and quantum mechanics that represents the total energy of a system. In quantum mechanics, it is used to describe the energy of a system in terms of operators and is central to the formulation of time-dependent and time-independent Schrodinger's equations.
💡Wave-Particle Duality
Wave-particle duality is the concept in quantum mechanics that particles can exhibit both wave-like and particle-like properties. This duality is a core principle that helps explain phenomena such as interference and diffraction patterns observed with particles like electrons in experiments like the double-slit experiment.
Highlights

The video discusses the Schrödinger equation, a fundamental equation in quantum mechanics that describes the motion and energy of small particles.

Small particles, such as electrons, exhibit wave-like properties, behaving more like photons than traditional particles.

Schrödinger's equation was developed without a direct derivation, relying on assumptions and the best knowledge available at the time.

The distinction between photons and particles is often blurry, with both exhibiting similar behaviors.

The equation is used to make analogies between the behavior of photons and particles to predict their motion.

A wave equation was necessary to describe the wave-like properties of particles, despite the thin line between photons and particles.

The wave equation initially had no physical meaning until it was interpreted as a probability density function.

The probability density function is obtained by squaring the wave function, which must be complex with real and imaginary parts.

The squared wave function represents the probability of finding a particle at a certain location, with higher probabilities indicated by higher function values.

The wave function's physical meaning comes from its ability to represent the probability density, not its raw form.

The wave function can be expressed in terms of position and time, incorporating the wave number and frequency.

The wave function takes the form of an amplitude times e to the power of ikx, with k being the wave number and x the position.

The time dependency is introduced with the term minus Omega T, common in classical mechanics for describing waves.

The Schrödinger equation has been verified through experimental outcomes, matching theoretical predictions.

The confidence in the Schrödinger equation is high, as experimental data consistently aligns with the equation's predictions.

Future videos will delve into the Schrödinger equation's derivation, development, and application in various quantum mechanical scenarios.

The Schrödinger equation is essential for understanding the behavior of small, quantized particles like electrons and protons.

The video series aims to provide a comprehensive understanding of the Schrödinger equation and its practical applications.

Transcripts

Browse More Related Video

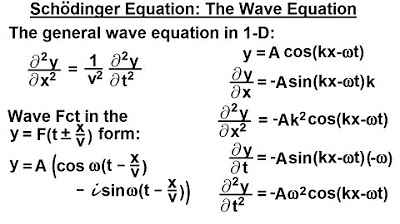
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (3 of 92) The Wave Equation

what is the radius of the hydrogen atom?

Quantum Mechanics and the Schrödinger Equation

Lecture 5: Operators and the Schrödinger Equation

Lec-13 I Schrodinger wave question I Applied Chemistry I Chemical Engineering

What is the Schrödinger Equation? A basic introduction to Quantum Mechanics

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
QuantumMechanicsSchrodingerEquationWaveParticleDualityPhysicsEducationPhotonBehaviorProbabilityDensityWaveFunctionQuantizationHistoricalPerspectiveScientificAnalogiesEducationalVideo