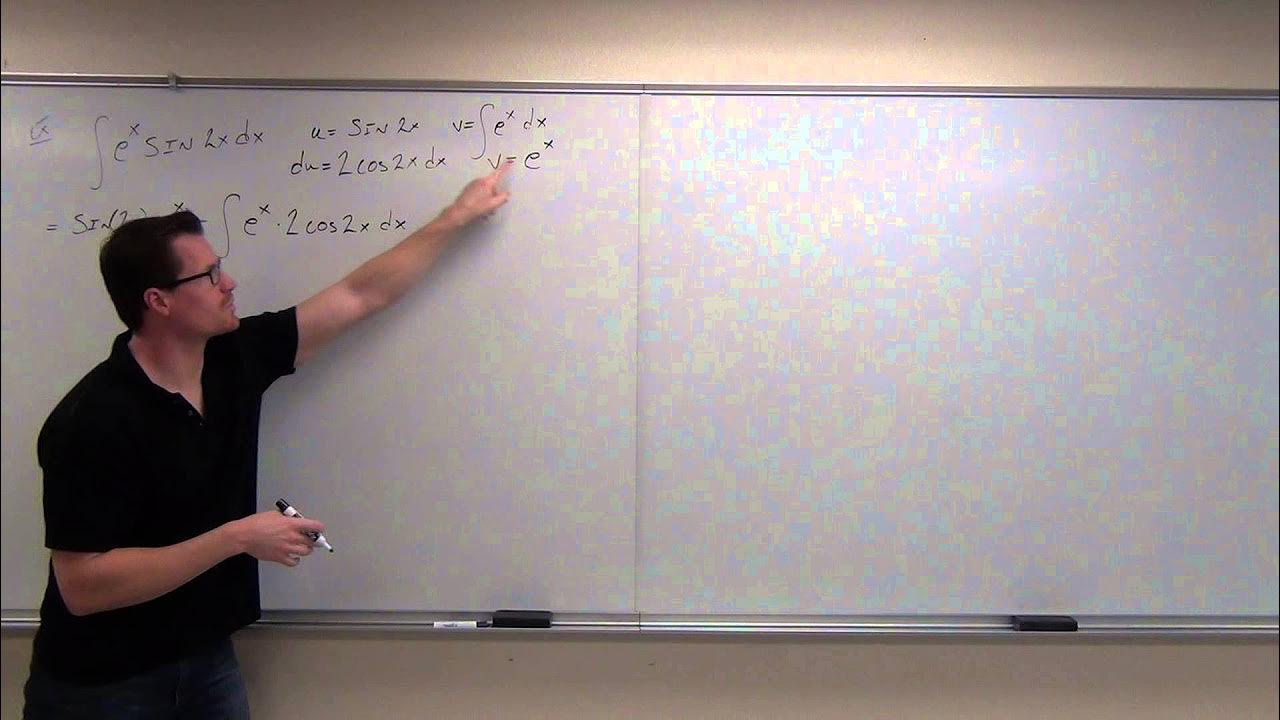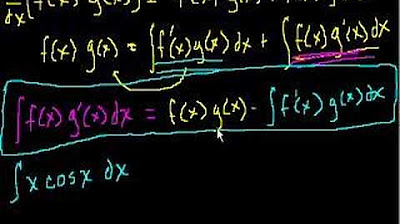Calculus BC – 6.11 Integrating Using Integration by Parts

The Algebros
4 Aug 202112:30
EducationalLearning
32 Likes 10 Comments

TLDRIn this engaging calculus lesson, Mr. Bean introduces integration by parts, a technique akin to the product rule for derivatives. He emphasizes the importance of correctly identifying the functions f and g' to apply this method effectively. Through examples, he demonstrates how to integrate complex functions and highlights the use of tabular integration for multiple steps, offering strategies for simplifying the process and saving time. The lesson concludes with a reminder to be mindful of potential shortcuts on AP exams.

Takeaways
  • 📘 Integration by parts is introduced as a calculus technique, analogous to the product rule for derivatives.
  • 🎓 The formula for integration by parts is ∫fg' = fg - ∫f'g, where f' and g' represent the derivatives of f and g, respectively.
  • 🔍 The choice of f and g' in integration by parts is crucial; f should become simpler upon differentiation, and g' should be easily integrable.
  • 🌟 The video provides a strategy for selecting f and g': choose f to be a function that simplifies when differentiated and g' to be a function that is easily integrated.
  • 📚 The product rule is referenced as the basis for deriving the integration by parts formula, linking back to an earlier lesson (2.8).
  • 📝 An example is worked through using integration by parts, integrating ∫x * sin(x)dx by choosing x as f and sin(x) as g'.
  • 🌐 The concept of tabular integration is introduced as a method to speed up the process when multiple integration by parts steps are required.
  • 🔗 Tabular integration involves creating a table with f's derivatives leading to zero and integrating g' in a diagonal pattern, alternating signs.
  • 📊 The video concludes with an example of tabular integration, integrating ∫x^4 * sin(x)dx and breaking down the process into a series of steps that fill out the table.
  • 💡 A tip is given for AP exam takers: be aware of intermediary steps in multiple-choice answers, as they may indicate the correct stopping point for the integration process.
  • 🎓 The lesson emphasizes the importance of practice and problem-solving to master integration by parts and tabular integration techniques.
Q & A

  • What is the main topic of this calculus lesson?

    -The main topic of this lesson is integration by parts, a technique used in calculus to integrate the product of two functions.

  • How does Mr. Bean relate integration by parts to a previously learned concept?

    -Mr. Bean relates integration by parts to the product rule for derivatives, which was taught in an earlier lesson (lesson 2.8), highlighting the similarity in their application.

  • What are the general steps involved in the integration by parts process?

    -The general steps involve choosing functions f and g', where f becomes simpler when differentiated, and g' can be easily integrated. The integral of the product of f and g' is then expressed as f times g minus the integral of the derivative of f times g.

  • Why does Mr. Bean prefer using f and g instead of u and v in his explanation?

    -Mr. Bean prefers using f and g because they are more distinct from each other, reducing the chance of confusion that might arise if u and v were used, especially when students are not careful with their notation.

  • What is the significance of identifying the correct f and g' in integration by parts?

    -Identifying the correct f and g' is crucial because it determines the success of the integration process. The choice affects how easily the integral and derivative can be calculated, which in turn affects the efficiency and accuracy of the integration by parts method.

  • How does the process of tabular integration help simplify complex integration problems?

    -Tabular integration organizes the integration process into a table format, which helps to streamline the repetitive steps involved in multiple integration by parts calculations. It saves time by reducing the need to write out each step individually and helps to maintain a clear overview of the process.

  • What is the pattern for the signs in the tabular integration method?

    -The pattern for the signs in tabular integration alternates between positive and negative, following a plus-minus-plus-minus pattern as you move across the rows of the table.

  • How does Mr. Bean derive the formula for integration by parts from the product rule?

    -Mr. Bean derives the formula by starting with the product rule for derivatives, which gives him f'g + fg'. He then solves for fg', rearranges the terms, and integrates both sides to arrive at the integration by parts formula: ∫fg'dx = fg - ∫f'gdx.

  • What is an example of when tabular integration might not be the most efficient method?

    -Tabular integration might not be the most efficient when there are intermediary steps provided in a multiple-choice question on an AP exam. In such cases, it might be faster to stop at the provided step and not calculate the full, lengthy result.

  • What is the final result of the first example given in the lesson?

    -The final result of the first example is -x*cos(x) + sin(x) + C, where C is the constant of integration.

  • What strategy does Mr. Bean suggest for choosing f in integration by parts?

    -Mr. Bean suggests choosing f to be the function that becomes simpler when its derivative is taken. This makes the process of integration more efficient and manageable.

Outlines
00:00
📚 Introduction to Integration by Parts

This paragraph introduces the concept of integration by parts, a method for integrating the product of two functions. It is likened to the product rule for derivatives but with a twist: the integral of function f times the derivative of function g (not g itself). The explanation includes a derivation from the product rule and emphasizes the importance of correctly identifying the functions f and g prime for the integration process. The paragraph also provides a strategy for choosing f, which should become simpler upon differentiation, and mentions the potential confusion with using u and v instead of f and g in textbooks.

05:02
🔍 Applying Integration by Parts

In this paragraph, the speaker walks through the application of integration by parts using a specific example. The process involves identifying the functions f and g prime, and then applying the formula for integration by parts. The example demonstrates how to integrate the product of x and sine x, showing the steps to find the anti-derivative of g prime and the derivative of f. The paragraph concludes with the final answer, negative x cosine x plus the integral of cosine x, which simplifies to positive sine x plus a constant.

10:04
📈 Tabular Integration for Complex Cases

This paragraph discusses a technique called tabular integration, which is useful when dealing with complex integrals that may require multiple steps of integration by parts. The speaker uses the example of integrating x to the fourth power times sine x and explains how to identify f and g prime for this more complicated scenario. The process involves differentiating f until it reaches zero and integrating g prime repeatedly. The paragraph then introduces the tabular format, which organizes the integration process into a table and uses a pattern of plus and minus signs to simplify the calculation. The final answer is a combination of terms involving x to various powers and the trigonometric functions cosine and sine, all simplified and organized from the tabular integration method.

Mindmap
Keywords
💡Integration by Parts
Integration by Parts is a technique used in calculus to integrate the product of two functions. It is analogous to the product rule for derivatives but involves the integral of one function times the derivative of another. In the video, Mr. Bean illustrates this concept by showing that the integral of f*g' is equal to f*g - the integral of f'*g. This method is crucial for solving more complex integrals, especially those not directly solvable by basic integration techniques.
💡AB and BC Exams
The AB and BC exams refer to two different versions of the AP Calculus exam. The AB exam covers a subset of the BC curriculum, and the BC exam is more comprehensive. In the video, Mr. Bean mentions that the topic of Integration by Parts is specific to the BC exam, implying that AB students can choose to skip this lesson if they are not required to learn this for their exam.
💡Product Rule
The Product Rule is a fundamental rule in calculus for finding the derivative of a product of two functions. It states that the derivative of f(x)g(x) is f(x)g'(x) + f'(x)g(x). In the context of the video, Mr. Bean draws a parallel between the Product Rule and Integration by Parts, using the Product Rule to derive the formula for Integration by Parts.
💡u and v
In the context of Integration by Parts, u and v are commonly used as placeholders for the two functions being integrated. The formula is often written as ∫u dv = uv - ∫v du. Mr. Bean, however, prefers to use f and g (or f and g') to avoid confusion, as u and v can look too similar and cause mistakes in understanding the functions' roles.
💡Derivative
A derivative is a fundamental concept in calculus that represents the rate of change of a function with respect to its independent variable. In the video, derivatives are used to find the 'prime' or differentiated form of a function, which is essential for applying Integration by Parts and understanding the Product Rule.
💡Anti-Derivative
An anti-derivative, also known as an indefinite integral, is the reverse process of differentiation. It is used to find the original function whose derivative is given, by reversing the process of taking the derivative. In the video, Mr. Bean uses anti-derivatives to find the integral of functions like sine and cosine, which are essential steps in solving integration problems.
💡Tabular Integration
Tabular Integration is a method used to simplify the process of repeated integration by parts. It organizes the integration process in a table format, which helps in keeping track of the steps and the alternating signs of the terms. This technique speeds up the calculation when dealing with complex integrals that would otherwise require multiple steps of Integration by Parts.
💡Differentiation
Differentiation is the process of finding the derivative of a function, which gives the rate at which a quantity changes with respect to another. It is a fundamental operation in calculus and is used to analyze functions' behavior, such as their slope, maximums, and minimums. In the video, differentiation is used to find the 'f' part in Integration by Parts.
💡Mastery Check
A Mastery Check is a method used in educational settings to assess a student's understanding and proficiency in a particular subject or topic. In the context of the video, Mr. Bean likely refers to a practice problem or quiz that students can complete to test their grasp of the Integration by Parts concept.
💡AP Exam
The AP Exam, or Advanced Placement Exam, is a standardized test in the United States that high school students can take to demonstrate their knowledge and skills in a variety of subjects, including calculus. In the video, Mr. Bean tailors his lesson to both AB and BC calculus students, who are preparing for different versions of the AP Calculus Exam.
💡Sine and Cosine Functions
Sine and cosine are trigonometric functions that describe periodic changes in right-angled triangles and are widely used in mathematics, physics, and engineering. In the video, Mr. Bean uses sine and cosine functions to demonstrate the process of Integration by Parts and to find the anti-derivatives of these functions.
Highlights

Introduction to Integration by Parts for BC Calculus students.

Integration by Parts is analogous to the Product Rule for derivatives.

The formula for Integration by Parts: ∫fg' = fg - ∫f'g.

Deriving Integration by Parts from the Product Rule, which was taught in Lesson 2.8.

Preferring f and g over u and v to avoid confusion in notation.

Strategy for choosing f: select a function that simplifies upon differentiation.

Strategy for choosing g': select a function that can be easily integrated.

Example of integrating x * sin(x) using Integration by Parts.

Demonstration of solving the integral by identifying f and g' correctly.

Explanation of the anti-derivative of sine x and its application in the example.

Final answer for the example: -x*cos(x) + sin(x) + C.

Introduction to Tabular Integration as a method to speed up the process.

Tabular Integration is particularly useful for multiple steps of Integration by Parts.

Step-by-step demonstration of Tabular Integration using x^4 * sin(x) as an example.

Explanation of the pattern for plus and minus signs in Tabular Integration.

Final complex answer using Tabular Integration: x^4*(-cos(x)) + 4x^3*(sin(x)) - 12x^2*cos(x) + 24x*(sin(x)) - 24*cos(x) + C.

Note on the AP Exam: sometimes an intermediary step is provided in multiple-choice questions, so students should be aware and not always go for the most expanded answer.

Conclusion and encouragement for students to practice and master Integration by Parts and Tabular Integration.

Transcripts

Browse More Related Video

AP Calculus BC Lesson 6.11

Calculus 2 Lecture 7.1: Integration By Parts

Indefinite Integration (part V)

Calculus AB/BC – 7.2 Verifying Solutions for Differential Equations

Calculus AB/BC – 5.8 Sketching Graphs of Functions and Their Derivatives

Calculus AB/BC – 6.9 Integrating Using Substitution

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusIntegration by PartsBC CurriculumMath EducationMr. BeanProduct RuleTabular IntegrationAP ExamMath StrategiesOnline Learning