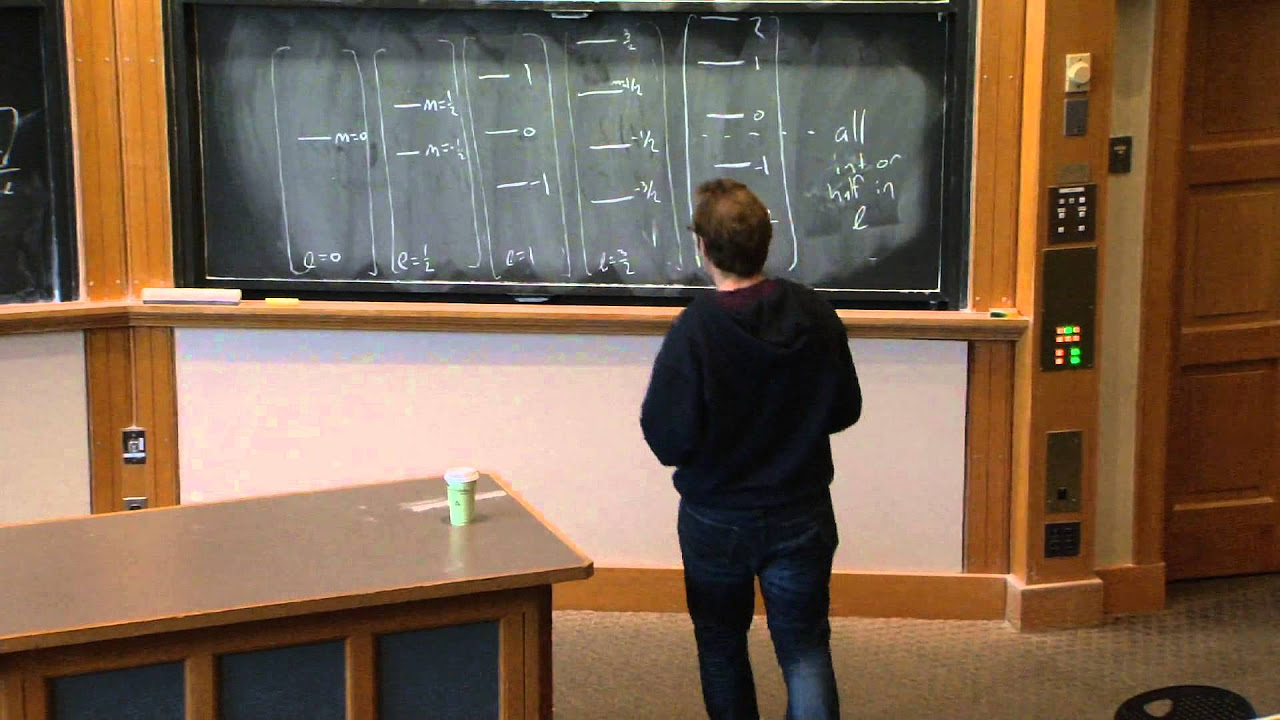12. Atoms in External Fields IV and Atom-light Interactions I
TLDRThis lecture delves into the ac Stark effect, exploring its impact on the absorption coefficient and the oscillator strength's role in parametrizing matrix elements. The professor discusses the relationship between quantum mechanics and classical physics in the context of the ac Stark effect, addressing misconceptions about matrix elements and oscillator strengths. The lecture also covers the coupling mechanisms between atoms and electromagnetic fields, including electric dipole, magnetic dipole, and electric quadrupole transitions, highlighting the importance of understanding higher-order processes and selection rules in atomic physics.
Takeaways
- 📚 The lecture discusses the ac Stark effect and its relation to perturbation theory, highlighting the importance of matrix elements in quantum mechanics.
- 🔗 The professor explains how the oscillator strength is a way to parametrize the matrix element, connecting quantum mechanical treatments of atoms to classical harmonic oscillators.
- 🌐 The dipole approximation is a key concept for understanding atomic transitions, and the script explores its limitations and the conditions under which it applies.
- 🤔 A question is raised about reconciling large matrix elements in Rydberg atoms with the sum rules of oscillator strengths, emphasizing the need for careful consideration of quantum states.
- 🔍 The lecture delves into the relationship between the index of refraction, polarizability, and the response of atoms to electromagnetic radiation, including the effects of dissipation.
- 🌟 The script introduces the concept of parametrizing the matrix element with a correlated gamma to understand the interaction of a laser beam with an atomic medium.
- 📈 The importance of the imaginary part of the index of refraction for absorption and the real part for dispersion is explained, showing how these lead to exponential absorption of light.
- 🧲 The discussion moves to higher-order radiation processes, such as magnetic dipole and electric quadrupole transitions, which become relevant when dipole transitions are forbidden.
- 💡 The professor illustrates how the magnetic moment operator and the electric quadrupole operator arise from the interaction Hamiltonian in the presence of electromagnetic fields.
- 🚫 Forbidden transitions are explained as those that are suppressed in leading order but become allowed at higher orders, often associated with weak matrix elements.
- 🔄 The lecture concludes with an introduction to selection rules, which classify possible transitions based on symmetry and angular momentum considerations.
Q & A
What is the main topic of the lecture?
-The main topic of the lecture is the interaction of atoms with electric and magnetic fields, specifically focusing on the ac Stark effect and its implications on atomic transitions and the absorption coefficient.
What is the ac Stark effect?
-The ac Stark effect refers to the shift in the energy levels of an atom due to the interaction with an external alternating electric field, which is different from the perturbation theory.
What is the role of the oscillator strength in the context of the lecture?
-The oscillator strength is a parameter that connects the quantum mechanical treatment of an atom to the response of a classical harmonic oscillator through the charge of an external field. It is used to describe the probability of an electronic transition and is related to the matrix element of the transition.
What is the significance of the matrix element in atomic transitions?
-The matrix element is crucial in describing the interaction between different states of an atom. It is involved in the calculation of transition probabilities and is directly related to the strength of transitions, such as electric dipole, magnetic dipole, and electric quadrupole transitions.
How does the lecture relate the concept of the matrix element to the index of refraction?
-The lecture connects the matrix element to the index of refraction by discussing how the polarizability of an atom, which depends on the matrix element, affects the index of refraction. This relationship is important for understanding how light interacts with and propagates through a medium.
What is the dipole approximation and why is it used?
-The dipole approximation is an assumption made when the wavelength of the electromagnetic field is much larger than the size of the atom, allowing the vector potential to be approximated as being position-independent. It simplifies calculations and is valid for most atomic transitions involving low-frequency fields.
What are the conditions for the sum rule of oscillator strengths?
-The sum rule for oscillator strengths states that the sum of all oscillator strengths for an atom must equal 1. This rule is particularly useful for the ground state, where all transitions are to higher energy levels, and thus all oscillator strengths are positive.
How does the lecture address the issue of 'forbidden' transitions?
-The lecture explains that 'forbidden' transitions are not strictly forbidden but are transitions that are weak and do not appear at the leading order of approximation. They become allowed when higher-order terms or relativistic effects are considered.
What is the relationship between the matrix element and the absorption coefficient?
-The matrix element is related to the absorption coefficient through the oscillator strength and the transition probability. A larger matrix element generally leads to a higher probability of transition and, consequently, a larger absorption coefficient for the corresponding transition.
How does the lecture discuss the higher-order radiation processes?
-The lecture discusses higher-order radiation processes by examining the terms beyond the dipole approximation, such as the magnetic dipole and electric quadrupole transitions. These higher-order terms become significant when the dipole transition is forbidden or weak.
What is the significance of the Bohr magneton in the context of magnetic dipole transitions?
-The Bohr magneton is a physical constant that expresses the magnetic moment of an electron due to its orbital motion. In the context of magnetic dipole transitions, the interaction matrix element is proportional to the Bohr magneton, indicating the strength of the coupling between the atom's magnetic moment and the magnetic field of the electromagnetic wave.
What is the difference between electric dipole and magnetic dipole transitions?
-Electric dipole transitions are caused by the interaction of an atom with the electric field of an electromagnetic wave, while magnetic dipole transitions involve the interaction with the magnetic field component of the wave. Electric dipole transitions are generally stronger and allowed, whereas magnetic dipole transitions are weaker and often 'forbidden' at the leading order.
How are selection rules related to the concept of spherical tensors?
-Selection rules are used to determine whether a transition between two states is allowed or forbidden based on symmetry considerations. Spherical tensors are used to decompose operators into components that transform under rotations like spherical harmonics. The selection rules for transitions can be determined by whether the sum of angular momenta of the initial and final states and the operator (spherical tensor) satisfies the triangle rule.
Outlines
📚 Introduction to MIT OpenCourseWare and Class Topic
The script begins with an introduction to the MIT OpenCourseWare initiative, which offers free educational resources under a Creative Commons license. The professor then promptly starts the class, revisiting the topic of the ac Stark effect discussed in the previous session and outlines the agenda for the day, which includes a deeper dive into the matrix element and its relation to the ac Stark effect and absorption coefficient. The professor also hints at the oscillator strength and its connection to the quantum mechanical treatment of an atom and the response of a classical harmonic oscillator.
🔬 Matrix Elements and Oscillator Strengths
This paragraph delves into the concept of matrix elements and oscillator strengths. The professor explains how the matrix element is a key parameter in quantum mechanics, particularly in the context of transitions between atomic states. The discussion includes the parametrization of matrix elements and their relation to semi-classical physics. The professor also addresses the misconception about the limits of matrix elements based on oscillator strengths, especially in the context of Rydberg atoms, which can have large matrix elements despite the sum rule for oscillator strengths.
🔍 The Relationship Between Polarizability and Index of Refraction
The professor explores the relationship between polarizability and the index of refraction, explaining how polarizability influences the index of refraction and how this relationship is derived from perturbation theory. The discussion also touches on the concept of dissipation and its impact on the polarizability of an atomic medium, leading to an understanding of how a laser beam interacts with such a medium, including the absorption and phase shift effects.
🌌 The Impact of Atomic Interactions with Light
This section discusses the impact of atomic interactions with light, focusing on the coupling matrix in an atom and the off-diagonal matrix elements that cause transitions. The professor explains the Hamiltonian between states and how the off-diagonal matrix element leads to the ac Stark effect. The discussion also introduces the concept of Rabi oscillations and transitions, highlighting the importance of the matrix element in understanding these phenomena.
🔧 Derivation of the Interaction Hamiltonian
The professor provides a detailed derivation of the interaction Hamiltonian, starting from the canonical coupling between electromagnetic fields and atoms. The derivation involves modifying the momentum operator with the vector potential and considering the kinetic energy in the Hamiltonian. The Coulomb gauge is used to simplify the calculations, and the interaction Hamiltonian is obtained by considering the coupling of momentum to the vector potential.
🌐 Expansion of the Plane Wave and Dipole Approximation
The script moves on to discuss the expansion of the plane wave and the concept of the dipole approximation. The professor explains how the leading term in this expansion results in the dipole approximation, which is valid when the atom is smaller than the wavelength of the electromagnetic field. The discussion also touches on higher-order terms that can lead to magnetic dipole and electric quadrupole transitions.
📐 Transitions Between Atomic States and Selection Rules
The final paragraph introduces the concept of selection rules in quantum mechanics, which are used to classify possible transitions between atomic states based on symmetry. The professor discusses how angular momentum is a key quantum number for classifying atomic states and how operators can be expanded into spherical tensors to analyze matrix elements. The importance of the triangle rule and the conservation of angular momentum in determining the validity of transitions is highlighted.
Mindmap
Keywords
💡ac Stark effect
💡oscillator strength
💡matrix element
💡Rydberg atoms
💡sum rule
💡index of refraction
💡polarizability
💡damping
💡dipole approximation
💡magnetic dipole and electric quadrupole transitions
Highlights
The ac Stark effect and its impact on the absorption coefficient were discussed, which is crucial for understanding how light interacts with atoms.
Oscillator strength was explained as a way to parametrize the matrix element, connecting quantum mechanical treatment of an atom to classical physics.
The relationship between the matrix element and the Bohr radius was explored, emphasizing the role of the dipole approximation in atomic transitions.
A detailed discussion on the sum rule for oscillator strengths and its implications for strong transitions in atoms was provided.
The distinction between the matrix elements of Rydberg atoms and the sum rules of oscillator strengths was clarified.
The index of refraction and its connection to polarizability were discussed, highlighting the impact of atomic density on light propagation.
A demonstration of how to derive the full expression for a laser beam crossing an atomic medium was presented.
The concept of parametrizing the matrix element by gamma and its role in the index of refraction was introduced.
The significance of the imaginary part of the index of refraction in causing absorption of light was explained.
The relationship between the optical density, phase shift, and the thickness of the medium was discussed in the context of laser beam propagation.
The coupling matrix in an atom and its role in state transitions were explored, moving beyond the semi-classical electromagnetic field formulation.
A brief derivation of the canonical coupling between electromagnetic fields and atoms was provided, emphasizing the role of the vector potential.
The dipole approximation was derived, showing its equivalence to the electric field times position operator.
The higher order radiation processes, such as magnetic dipole and electric quadrupole transitions, were introduced and differentiated from the dipole approximation.
The concept of selection rules in atomic transitions was introduced, providing a framework for classifying possible transitions based on symmetry.
The impact of relativistic effects on allowing certain transitions, such as the singlet to triplet transition in helium, was discussed.
The lecture concluded with an overview of how angular momentum conservation rules apply to the selection rules of atomic transitions.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: