Mirror Formula and Magnification | Sign Convention
TLDRThis educational video script explores the principles of image formation by spherical mirrors, contrasting the traditional ray diagram method with a formulaic approach using sign conventions. It explains the mirror formula and magnification, providing clear examples for concave and convex mirrors. The script aims to clarify the concepts and empowers viewers to calculate unknown parameters, emphasizing practice for better understanding.
Takeaways
- 🔍 The video discusses two methods for predicting the position and properties of an image formed by a spherical mirror: ray diagrams and formulae.
- 📚 The formula method is highlighted as more powerful because it allows for easy calculation of the third unknown when two variables are known.
- 📏 Sign conventions for spherical mirrors are crucial and dictate the positive or negative values of object and image distances, heights, and focal lengths.
- 📐 The mirror formula \( \frac{1}{v} + \frac{1}{u} = \frac{1}{f} \) is introduced, where \( v \) is the image distance, \( u \) is the object distance, and \( f \) is the focal length.
- 🔄 Magnification is defined as the ratio of the image height to the object height and can be calculated using the formula \( m = -\frac{v}{u} \).
- 🖼️ The script provides examples to illustrate how to apply the sign convention and formulae to concave and convex mirrors.
- 🤔 The video emphasizes the importance of understanding sign conventions for accurate calculations in mirror imaging.
- 📉 The magnification formula helps determine whether an image is real, virtual, inverted, or diminished.
- 📈 The script includes step-by-step problem-solving using the mirror formula and magnification to find unknown variables.
- 📝 Practice is recommended for mastering the concepts of sign convention and mirror formulae application.
- 🌐 The video concludes by directing viewers to Manoj Academy for further learning resources in various subjects.
Q & A
What is the principal axis in the context of a concave mirror?
-The principal axis is an imaginary line that passes through the center of the mirror and is used as a reference for the positions of the object and the image.
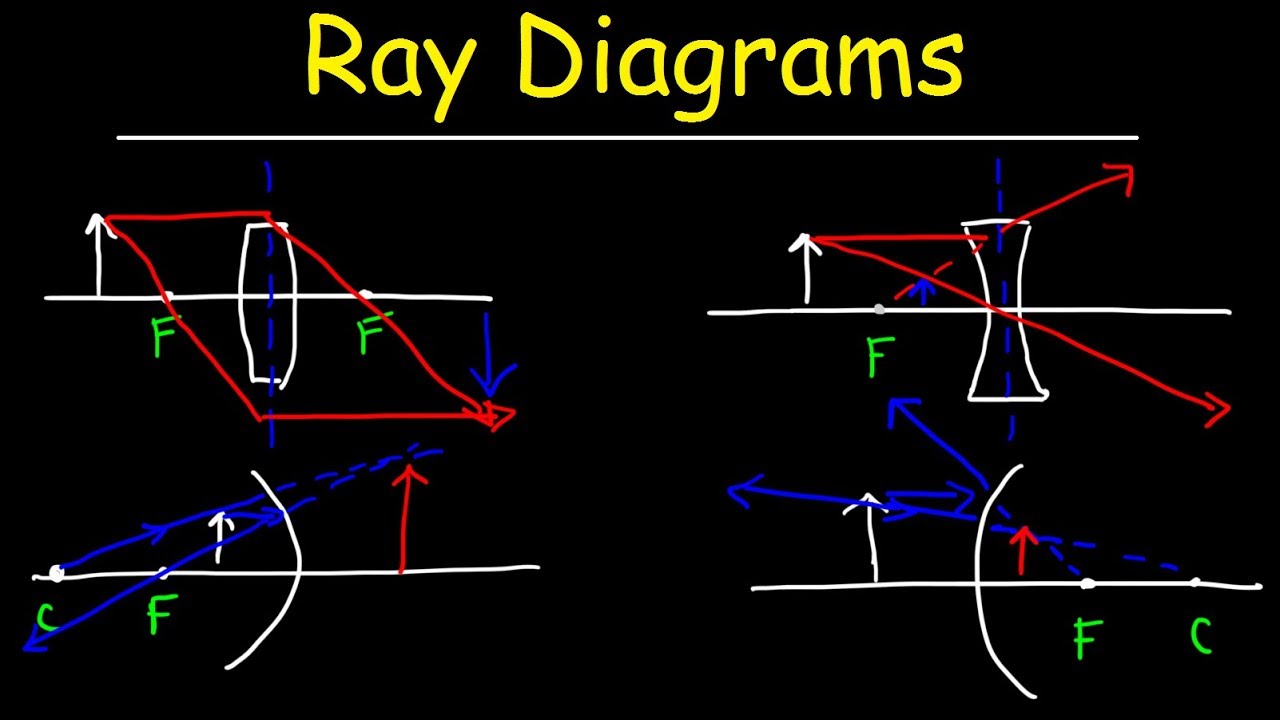
What are the two methods discussed in the script for predicting the nature and position of an image formed by a mirror?
-The two methods discussed are using ray diagrams and applying sign conventions along with mathematical formulae.
What is the significance of the sign convention in spherical mirrors?
-The sign convention helps in determining whether the distances, object, image heights, and focal length are positive or negative, which is crucial for accurately calculating the position and nature of the image using formulae.
What is the mirror formula, and how is it used?
-The mirror formula is \( \frac{1}{v} + \frac{1}{u} = \frac{1}{f} \), where \( v \) is the image distance, \( u \) is the object distance, and \( f \) is the focal length. It is used to calculate the unknown distances when two of these are known.
How is magnification defined in the context of mirror imaging?
-Magnification (m) is the ratio of the image height (\( h' \)) to the object height (h), and it indicates how much larger or smaller the image is compared to the object.
What does a negative magnification value signify in the context of mirror imaging?
-A negative magnification value indicates that the image is inverted compared to the object.
What is the relationship between the object distance, image distance, and focal length for a concave mirror?
-For a concave mirror, the object distance is typically negative (since it's on the left side of the mirror), the image distance can be positive (real image) or negative (virtual image), and the focal length is negative (focus in front of the mirror).
How can you determine the position and nature of the image formed by a convex mirror?
-By using the mirror formula and magnification formulae, you can determine if the image is virtual, real, its position relative to the mirror, and whether it is magnified, diminished, or the same size as the object.
What is the formula that relates magnification to the image and object distances?
-The formula that relates magnification to the image and object distances is \( m = -\frac{v}{u} \), where \( m \) is the magnification, \( v \) is the image distance, and \( u \) is the object distance.
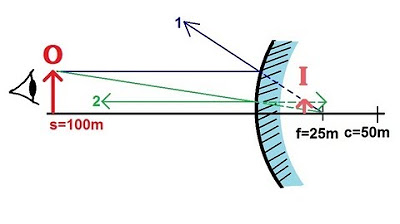
Can you provide an example of how to use the sign convention and formulae to find the image properties for a concave mirror?
-Sure. If an object is placed 15 cm from a concave mirror with a focal length of 10 cm, using the mirror formula, you would find the image distance to be 30 cm in front of the mirror (real image). The magnification formula would then tell you the size and orientation of the image.
Outlines
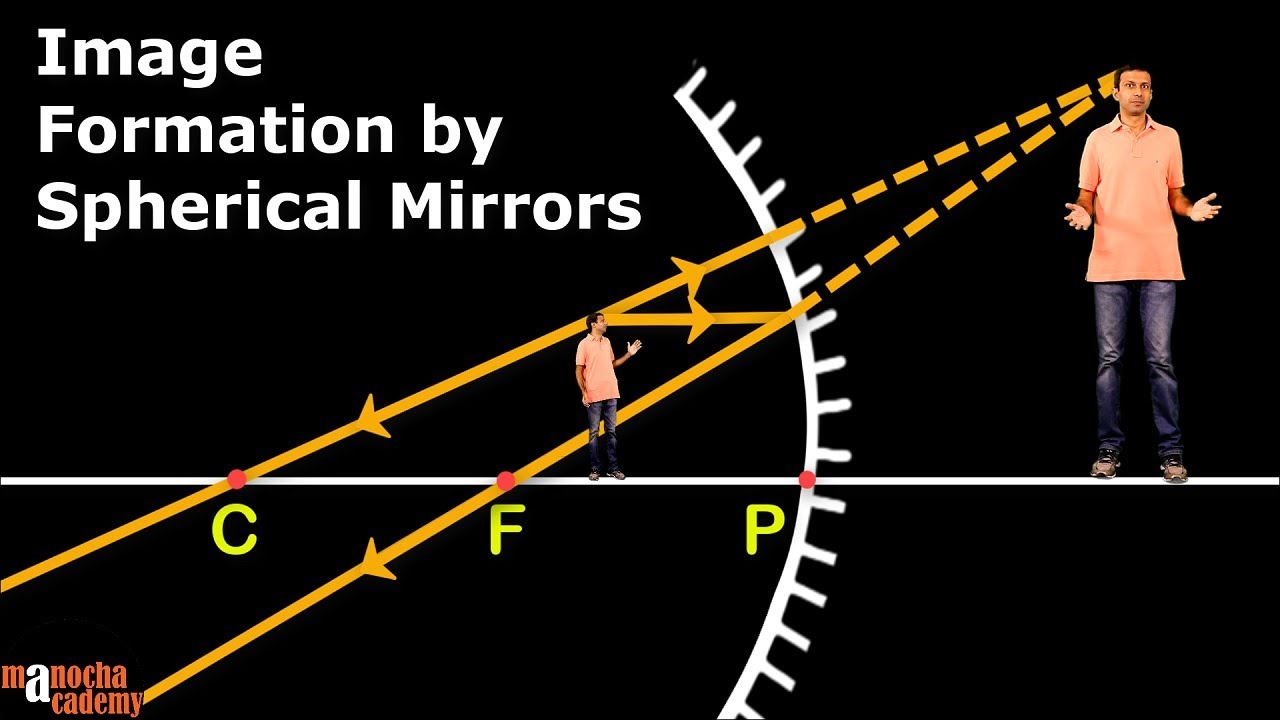
🔍 Introduction to Spherical Mirrors and Image Formation
The script introduces the concept of image formation by spherical mirrors, specifically focusing on a concave mirror. It explains the use of light ray rules and ray diagrams to predict the position and properties of the image. The video aims to teach a formula-based approach using sign conventions and mirror formulas, which is more powerful for calculating unknowns when some parameters are known. The script emphasizes the importance of understanding sign conventions for both concave and convex mirrors when using the coordinate system with the origin at the mirror's pole.
📚 Understanding Sign Conventions and Mirror Formulas
This paragraph delves into the specifics of sign conventions for spherical mirrors, detailing how object and image distances, heights, and focal lengths are assigned positive or negative signs based on their position relative to the mirror. The mirror formula \( \frac{1}{v} + \frac{1}{u} = \frac{1}{f} \) is introduced, along with an example using a concave mirror to calculate image distance given the object distance and focal length. The paragraph also explains the concept of magnification, \( m = \frac{h'}{h} \), and provides examples to illustrate how it is calculated for both concave and convex mirrors.
📐 Applying Sign Conventions and Formulas in Examples
The script presents a step-by-step application of the sign conventions and mirror formulas through examples. It demonstrates how to find the image distance and magnification for a concave mirror when the object distance and focal length are given. The explanation includes the process of assigning signs to distances and heights, solving the mirror formula to find the image distance, and using magnification to determine the image size and orientation. The paragraph also introduces a formula relating magnification to image and object distances, providing a comprehensive understanding of spherical mirror calculations.
🎯 Solving Problems with Convex Mirrors and Final Thoughts
The final paragraph addresses a problem involving a convex mirror, where the object distance, object height, and image height are given, and the task is to find the focal length and image position. It guides the viewer through calculating magnification, using it to find the image distance, and then employing the mirror formula to determine the focal length. The script concludes by emphasizing the clarity of the concepts of sign conventions and mirror formulas, encouraging practice and offering resources for further learning on manojacademy.com.
Mindmap
Keywords
💡Concave mirror
💡Convex mirror
💡Ray diagram
💡Sign convention
💡Mirror formula
💡Focal length
💡Image distance (v)
💡Object distance (u)
💡Magnification
💡Real and virtual images
💡Principal axis
Highlights
Introduction to predicting image formation on the principal axis of a concave mirror using light ray rules and ray diagrams.
Exploration of a different approach to image formation using sign conventions and mirror formulae.
Explanation of the two types of spherical mirrors: concave and convex, and their image formation methods.
Demonstration of the formula method's power in calculating unknowns when two parameters are known.
Overview of the sign convention for spherical mirrors with a simple coordinate axis example.
Description of the mirror formula \( \frac{1}{v} + \frac{1}{u} = \frac{1}{f} \) and its components.
Application of the mirror formula through an example with given object distance and focal length.
Introduction to magnification formulae and their significance in determining image size and orientation.
Example illustrating how to calculate magnification using object and image heights.
Explanation of how the sign of magnification indicates the image's inversion.
Derivation of a formula relating magnification to image and object distances.
Presentation of four key formulae for spherical mirrors and their applications.
Step-by-step guide to solving for image properties using sign convention and mirror formulae.
Example problem solving for a concave mirror with given object size and distance.
Example problem solving for a convex mirror to find focal length and image position.
Emphasis on practicing problems to solidify understanding of sign conventions and formulae.
Promotion of Manoj Academy's full courses for various subjects and the provided links for further learning.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: