Geometric Series BC Calculus 1-31

Chad Gilliland
30 Jan 201314:23
EducationalLearning
32 Likes 10 Comments

TLDRThis video script delves into the intricacies of series convergence tests, highlighting the N-term test's limitations and introducing alternative methods such as the geometric series test and the telescoping series. The instructor emphasizes that the N-term test can only confirm divergence, not convergence, and proceeds to demonstrate how to apply geometric series tests to determine both convergence and the sum of the series. The script also covers the concept of horizontal asymptotes and their role in series analysis, concluding with an exploration of infinite geometric series and their convergence properties.

Takeaways
  • 📚 The Nth Term Test is a quick method to determine if a series diverges by checking if the limit as \( n \) approaches infinity of \( a_n \) does not equal zero.
  • 🔍 If the Nth Term Test doesn't apply, further tests like the Geometric Series Test and the Telescoping Series Test can be used to determine convergence.
  • 📉 For a series to diverge, the limit of its nth term must not be zero, according to the Nth Term Test.
  • 📈 The Horizontal Asymptote Theorem states that if the degree of the polynomial in the numerator matches the degree in the denominator, the limit as \( n \) approaches infinity is the ratio of the leading coefficients.
  • 🔢 In the script, the series \( e^{1/3} \) was used as an example of a geometric series, showing that if the common ratio \( r \) is between -1 and 1, the series converges to \( \frac{a_1}{1 - r} \).
  • 🌐 The script explains that a series like \( \frac{1}{n^2 + n} \) does not apply to the Nth Term Test and requires further analysis, which will be covered later.
  • 🔬 The Telescoping Series is identified, where terms cancel each other out, leading to a simplified sum, as demonstrated with the series \( \frac{1}{n - 1/(n + 1)} \).
  • 📊 A geometric series with a common ratio greater than one, such as \( 3^n \), is divergent and grows without bound.
  • 🧩 The script also discusses the transformation of a series into a geometric series by factoring out constants and simplifying the terms.
  • 💡 The concept of a repeating decimal being represented as an infinite geometric series is introduced, with the example of 0.999... being equal to 1.
  • 🚫 The script emphasizes that the Nth Term Test cannot be used to argue for convergence, only to determine divergence.
Q & A

  • What is the main purpose of the Nth term test for series?

    -The Nth term test is used to quickly determine if a series diverges. If the limit as n approaches infinity of the nth term of the series does not equal zero, the series diverges.

  • What is the limitation of the Nth term test?

    -The limitation of the Nth term test is that it can only be used to prove divergence. It cannot be used to prove convergence.

  • What are the two additional tests mentioned for determining convergence of a series?

    -The two additional tests mentioned for determining convergence are the Geometric Series Test and the Telescoping Series Test.

  • What is a geometric series and how does it converge?

    -A geometric series is a series where each term is a constant ratio (common ratio) raised to the nth power. It converges if the common ratio is between -1 and 1, and the sum can be found using the formula: first term / (1 - common ratio).

  • What is a telescoping series and how does it behave?

    -A telescoping series is a series where consecutive terms cancel each other out, leaving only the first term and the last term that does not get canceled. It converges to the value of the first term minus the last non-canceled term.

  • How does the horizontal ASM (Archimedes' method) theorem apply to the series in the script?

    -The horizontal ASM theorem states that if the limit as n approaches infinity of the ratio of the leading coefficients of the highest degree terms of two polynomials is not equal to zero, then the series diverges.

  • What is the significance of the limit of a series' nth term approaching zero?

    -If the limit of a series' nth term as n approaches infinity is zero, it suggests that the series could potentially converge, but further tests are needed to confirm convergence.

  • What happens when the common ratio of a geometric series is greater than one?

    -If the common ratio of a geometric series is greater than one, the series diverges because the terms do not approach zero and instead grow larger.

  • How can you determine if a series is a geometric series in disguise?

    -A series can be a geometric series in disguise if it can be rewritten with a common ratio raised to the nth power, even if there are additional factors or terms that can be factored out or simplified.

  • What is the sum of an infinite geometric series with a common ratio of 1/10?

    -The sum of an infinite geometric series with a common ratio of 1/10 is the first term divided by (1 - common ratio), which in this case is 9/10 / (1 - 1/10), simplifying to 1.

  • Why do factorials outgrow exponentials in series?

    -Factorials outgrow exponentials in series because the growth rate of factorials is super-exponential, increasing much faster than exponential functions, leading to divergence.

Outlines
00:00
🔍 Introduction to Series Convergence Tests

This paragraph introduces the basic concept of series convergence and divergence using the nth term test. It explains that if the limit of a sequence as n approaches infinity is not zero, the series diverges. The paragraph also introduces the geometric series test and telescopic series, which will be discussed further if the nth term test does not apply.

05:01
📉 Geometric Series and Their Convergence

This section delves into the geometric series and how to determine if they converge. It explains that a geometric series converges if the common ratio is between -1 and 1. It provides an example where a series converges to a specific sum. The paragraph also covers the concept of the first term and common ratio in determining convergence.

10:03
🔭 Understanding Telescopic Series

This paragraph explains the telescopic series, using partial fractions to demonstrate how terms cancel out in a series, leading to a convergent sum. It provides an example of a telescopic series and shows the step-by-step process of how terms collapse to give the final sum.

🧮 Simplifying Complex Series

This section provides examples of how to simplify and determine the convergence of more complex series. It includes examples of geometric series in disguise and shows how to rewrite terms to identify common ratios. The paragraph also discusses how some series can be identified as divergent by the nth term test and the concept of factorials growing faster than exponentials.

🔢 Infinite Geometric Series

The final paragraph discusses infinite geometric series, using the example of 0.999... repeating. It explains how to rewrite such series, identify the common ratio, and determine their sum. The paragraph concludes by proving that 0.999... repeating equals 1, illustrating the concept of convergence in infinite geometric series.

Mindmap
Keywords
💡Nth Term Test
The Nth Term Test is a fundamental concept in the study of series, used to determine the convergence or divergence of an infinite series. It states that if the limit of the nth term of a series as n approaches infinity is not zero, then the series diverges. In the video, this test is used as a quick method to identify divergence, such as in the series where the limit of 'a sub n' is not zero, indicating divergence.
💡Convergence
Convergence refers to the property of a series where the sum of its terms approaches a finite limit as more terms are added. The video discusses the geometric series test and telescoping series as methods to determine convergence, in cases where the Nth Term Test does not apply.
💡Divergence
Divergence is the opposite of convergence; it describes a series where the sum of its terms grows without bound as more terms are added. The script uses the Nth Term Test to identify divergence, such as in the series where the limit as n approaches infinity of 'a sub n' does not equal zero.
💡Geometric Series
A geometric series is a type of series where each term is a constant multiple of the previous term. The video explains that a geometric series converges if the common ratio (the constant multiple) is between -1 and 1, and provides the formula for the sum of a convergent geometric series.
💡Telescoping Series
A telescoping series is a series where consecutive terms cancel each other out, leaving only a few terms that do not cancel. The script illustrates this with an example where the series collapses to a single term, converging to a specific value.
💡Horizontal Asymptote
A horizontal asymptote is a horizontal line that a function approaches as its input (or the variable) goes to infinity or negative infinity. In the context of the video, the horizontal asymptote is used to determine the behavior of the nth term as n approaches infinity, which helps in applying the Nth Term Test.
💡Common Ratio
The common ratio is the factor by which consecutive terms of a geometric series are multiplied. The video uses the common ratio to determine the convergence of a geometric series, stating that the series converges if the common ratio is between -1 and 1.
💡Factorial
Factorial, denoted by an exclamation mark (e.g., n!), is the product of all positive integers up to a given number n. The script mentions that factorials outgrow exponentials, indicating the rapid growth of terms involving factorials in a series, which often leads to divergence.
💡Partial Fractions
Partial fractions is a technique used to decompose a complex fraction into simpler fractions, which can then be more easily summed or analyzed. The video uses partial fractions to transform a series into a telescoping series, allowing for the determination of its convergence.
💡Exponential Growth
Exponential growth describes a situation where a quantity increases by a constant proportion over equal intervals of time. The video contrasts exponential growth with factorial growth, noting that factorials will always outpace exponential growth in series, leading to divergence.
💡Infinite Geometric Series
An infinite geometric series is a geometric series that continues indefinitely. The video discusses how to determine the sum of such a series if it converges, using the common ratio and the first term of the series as key components in the calculation.
Highlights

The N-term test for divergence: If the limit as n approaches infinity of a_subn does not equal zero, the summation from 1 to infinity of a_subn diverges.

The N-term test cannot be used to argue for convergence.

Introduction of the geometric series test and telescoping series as additional tests for convergence.

The horizontal ASM (Asymptote to the Sum) theorem and its application in determining divergence.

The limit of arctan(n) as n approaches infinity and its divergence based on the N-term test.

Geometric series identification and its convergence criteria based on the common ratio.

The formula for the sum of a convergent geometric series and how to determine its convergence value.

The bottom-heavy fraction concept and its implication on the N-term test's inapplicability.

Telescoping series explanation and demonstration of how it collapses to a single term.

Partial fractions technique in analyzing the convergence of a series.

The divergence of a geometric series with a common ratio greater than one.

The method to determine the convergence of a series by rewriting and factoring out constants.

The concept of infinite geometric series and its convergence to a specific value.

The demonstration that 0.9 repeating equals 1 using the properties of geometric series.

The divergence of series with factorial terms outgrowing exponential terms.

The importance of correctly applying the N-term test and understanding its limitations in series analysis.

Transcripts

Browse More Related Video

A Lot of Series Test Practice Problems

Calculus BC Unit 11 Recap

Calculus 2 - Geometric Series, P-Series, Ratio Test, Root Test, Alternating Series, Integral Test

Infinite Series Multiple Choice Practice for Calc BC (Part 6)

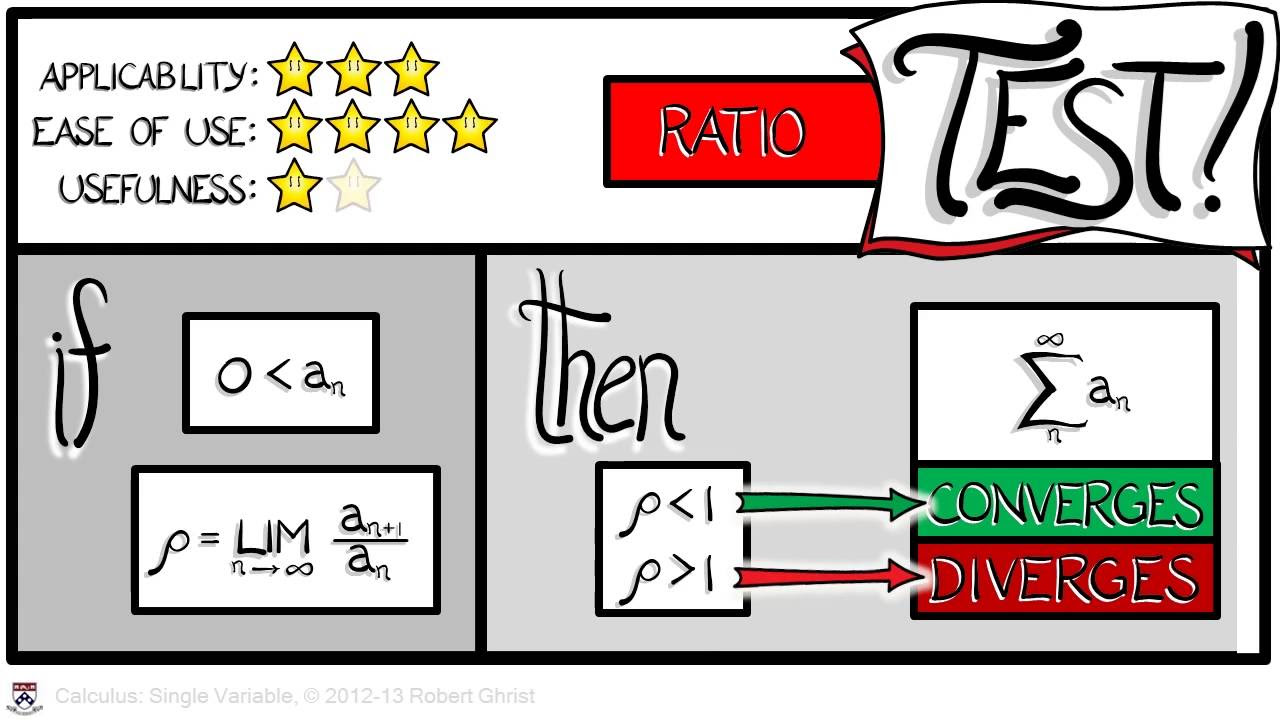
Calculus Chapter 5 Lecture 52 Convergence Tests 2

Unit 10 Study Guide - AP Calculus (BC Only)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Series AnalysisConvergence TestN-term TestGeometric SeriesTelescopic SeriesLimit CalculationMathematics EducationInfinite SeriesDivergence CheckFractional PowersEducational Content