Proving a sequence converges using the formal definition | Series | AP Calculus BC | Khan Academy
TLDRThis video script explores the proof of a sequence's convergence to zero. The sequence is defined as (-1)^{n+1} / n, and the presenter aims to demonstrate that as n approaches infinity, the sequence approaches zero. The proof involves the concept of epsilon-N definition, where for any given positive epsilon, there exists an N such that for all n > N, the sequence's terms are within epsilon of zero. The presenter successfully shows that by setting N = 1/epsilon, the sequence's terms will be less than epsilon, confirming its convergence to zero.
Takeaways
- 📚 The video discusses proving the limit of a specific sequence.
- 🔍 The sequence in question is defined as \( \frac{(-1)^{n+1}}{n} \).
- 🧩 The claim is that the limit of this sequence as \( n \) approaches infinity is 0.
- 🔎 The proof involves showing that for any \( \epsilon > 0 \), there exists an \( M \) such that for all \( n > M \), the sequence is within \( \epsilon \) of 0.
- 📉 As \( n \) increases, the sequence appears to get smaller, despite the numerator oscillating between -1 and 1.
- 📚 The proof strategy is to show that the absolute value of the sequence minus 0 (i.e., the sequence itself) is less than \( \epsilon \).
- 🔄 The sequence's absolute value simplifies to \( \frac{1}{n} \), which must be less than \( \epsilon \).
- 🔢 Taking the reciprocal of both sides of the inequality \( \frac{1}{n} < \epsilon \) gives \( n > \frac{1}{\epsilon} \).
- 📈 By setting \( M = \frac{1}{\epsilon} \), the condition for the sequence being within \( \epsilon \) of 0 is established for all \( n > M \).
- 🏁 The proof concludes that the sequence indeed converges to 0, as demonstrated by the relationship between \( n \), \( \epsilon \), and \( M \).
Q & A
What is the sequence being discussed in the transcript?
-The sequence being discussed is defined explicitly as (-1)^(n+1)/n.
What is the claim about the limit of the sequence?
-The claim is that the limit of the sequence as n approaches infinity is 0.
Why does the sequence appear to converge to 0?
-As n becomes larger, the numerator oscillates between -1 and 1, but the overall fraction gets smaller because it is divided by n, which increases without bound.
What needs to be proven to show the sequence converges to 0?
-To prove the sequence converges to 0, it must be shown that for any epsilon greater than 0, there exists a capital M such that if n is greater than M, the nth term of the sequence is within epsilon of 0.
How is the limit definition applied to prove convergence?
-The definition is applied by showing that the absolute value of the difference between a_n (the sequence term) and the limit (0) is less than epsilon for n greater than a certain M.
What role does epsilon play in proving the sequence's convergence?
-Epsilon represents an arbitrary positive distance from the limit (0). The proof shows that we can always find an M such that the sequence terms are within this distance for n > M.
What is the relationship between n and epsilon in the proof?
-For the sequence to be within epsilon of the limit, n must be greater than 1/epsilon.
How does taking the reciprocal affect the inequality in the proof?
-Taking the reciprocal of both sides of the inequality 1/n < epsilon results in n > 1/epsilon, reversing the inequality sign.
How does the proof demonstrate the sequence's convergence to 0?
-The proof demonstrates convergence by showing that for any epsilon > 0, choosing M = 1/epsilon ensures that for n > M, the sequence term is less than epsilon away from 0.
What is an example of epsilon and how is M determined from it?
-If epsilon is chosen as 0.5, then M would be 1/0.5, which is 2. For n > 2, the sequence terms are within 0.5 of the limit 0.
Outlines
📚 Proving the Limit of a Sequence
In this paragraph, the speaker aims to prove a claim made in a previous video regarding the limit of a specific sequence. The sequence in question is defined as (-1)^(n+1) / n, and the claim is that its limit as n approaches infinity is 0. The speaker explains that to prove this, they must show that for any given positive epsilon, there exists a positive integer M such that when n is greater than M, the absolute value of the nth term of the sequence minus 0 (the proposed limit) is less than epsilon. This is shown by demonstrating that 1/n must be less than epsilon, which leads to the conclusion that n must be greater than 1/epsilon. The proof is completed by setting M to 1/epsilon, ensuring that for any n greater than this value, the sequence's terms will be within epsilon of the limit, thus confirming the convergence to 0.
🔍 Demonstrating Convergence Beyond a Certain Point
Building upon the proof from the previous paragraph, this section illustrates the practical application of the proof by showing that for any chosen epsilon, such as 0.5, the sequence's terms will fall within the defined bounds for n greater than 1/(2*epsilon), which in this case is 2. The speaker demonstrates this by showing that for n equal to 3, 4, 5, and so on, the sequence's terms remain within the specified range, thus confirming the convergence to 0. The proof is not just theoretical; it is visually represented and proven to hold true for any given epsilon, reinforcing the validity of the claim that the sequence converges to 0 as n approaches infinity.
Mindmap
Keywords
💡Limit
💡Sequence
💡Convergence
💡Epsilon
💡M
💡Absolute Value
💡Reciprocal
💡Inequality
💡Oscillate
💡Proof
Highlights
The sequence defined as negative 1 to the power of n plus 1 over n is proven to have a limit of 0 as n approaches infinity.
The proof involves showing that for any given epsilon greater than 0, there exists an M such that the sequence's nth term is within epsilon of 0 for n greater than M.
The concept of epsilon-delta definition of a limit is introduced to formalize the convergence of the sequence to 0.
The graphical representation of epsilon bounds around the limit 0 is used to visualize the convergence.
The sequence's behavior is analyzed by considering the absolute value of the nth term minus 0, which simplifies to the absolute value of 1 over n.
The absolute value of the sequence's nth term is equated to 1 over n, setting the stage for the reciprocal relationship between n and epsilon.
The reciprocal of both sides of the inequality 1/n < epsilon is taken to find the condition for n in terms of epsilon.
The condition n > 1/epsilon is derived, which is a key step in proving the existence of the limit.
The proof concludes by setting M to 1/epsilon, ensuring that for any n greater than M, the sequence's nth term is within epsilon of 0.
The sequence's convergence to 0 is illustrated by choosing a specific epsilon value and demonstrating the sequence's behavior for n greater than M.
The proof is not just an assertion but a rigorous mathematical demonstration of the sequence's convergence.
The video provides a clear explanation of the steps involved in proving the limit of a sequence using the epsilon-delta definition.
The importance of the reciprocal relationship in establishing the limit condition for the sequence is emphasized.
The video demonstrates the practical application of mathematical concepts in proving the convergence of a sequence to a limit.
The proof process is made accessible by using visual aids and step-by-step explanations.
The video concludes with a confirmation of the sequence's convergence to 0, solidifying the proof.
Transcripts
Browse More Related Video

Formal definition for limit of a sequence | Series | AP Calculus BC | Khan Academy

Convergent and divergent sequences | Series | AP Calculus BC | Khan Academy

AP Calculus BC Lesson 10.3

Radius of convergence using Ratio Test

Integral test | Series | AP Calculus BC | Khan Academy
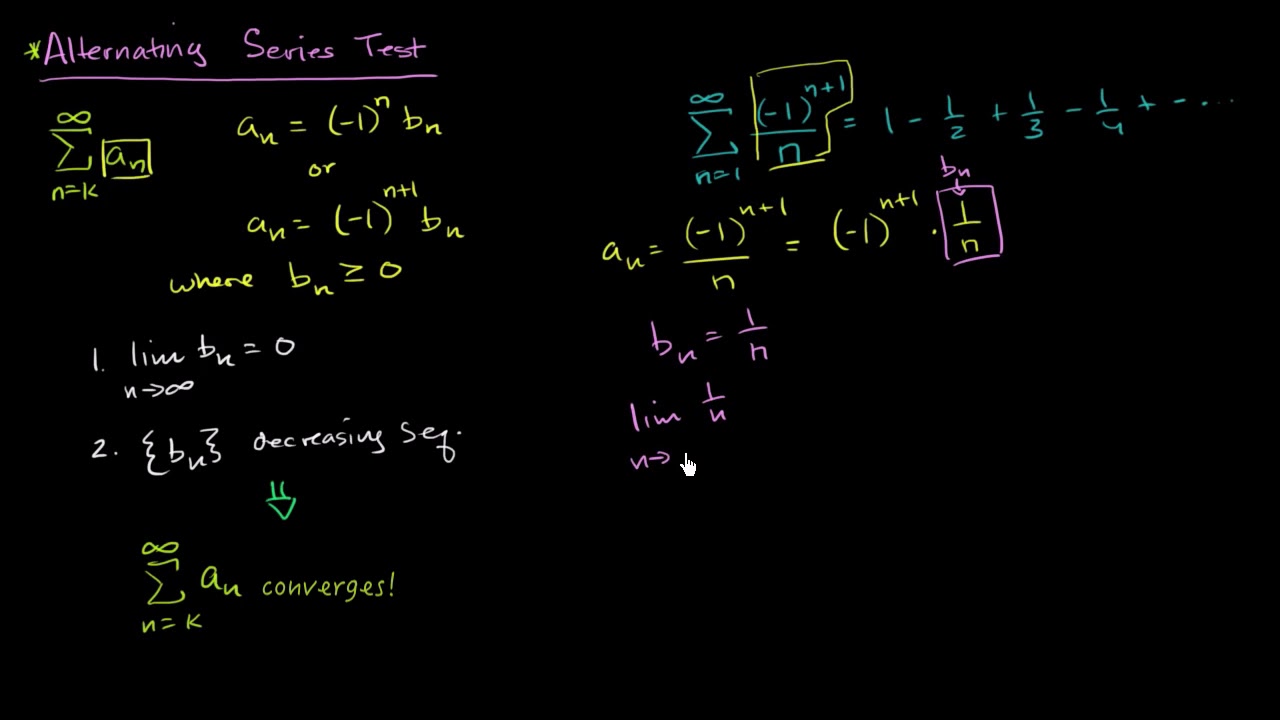
Alternating series test | Series | AP Calculus BC | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: