Distance and Displacement
TLDRThis video script delves into the concepts of distance and displacement through the lens of calculus. It explains how the Fundamental Theorem of Calculus can be applied to find the net change in position by integrating velocity over time, defining displacement. The script also clarifies the difference between speed and velocity, highlighting speed as the absolute value of velocity. It introduces the method to calculate total distance traveled by integrating speed and demonstrates how to use a calculator for definite integrals. The video provides step-by-step examples, including finding acceleration, position, and direction changes of particles, to solidify the understanding of these concepts.
Takeaways
- 📚 The video discusses the concepts of distance and displacement, integrating them with the fundamental theorem of calculus.
- 🔍 The integral of velocity between two time values is defined as the change in position, which is also referred to as displacement.
- 🏃♂️ Speed is defined as the absolute value of velocity, and it remains a key concept even when motion transitions from one-dimensional to two-dimensional space.
- 🚗 The total distance traveled is calculated by integrating speed over time, akin to how an odometer measures distance.
- 🧮 The video demonstrates how to compute definite integrals using a calculator, specifically on TI-83 and TI-84 models, which is crucial for solving problems in the class.
- 📉 The script uses an example from the 2018 Calculus AB free response section to illustrate how to find acceleration and position by integrating velocity.
- 📚 The video explains how to determine when two particles are moving with the same velocity by setting their velocity functions equal and solving for the intersection.
- 🔢 The script includes a detailed example of finding when a particle is moving to the left by analyzing the sign of its velocity.
- 📈 The video demonstrates how to determine if a particle is speeding up or slowing down by analyzing the product of its velocity and acceleration at a given time.
- 📌 The script concludes with an example from the 2016 Calculus AB free response section, showing how to find the position of a particle at a specific time and the total distance traveled.
Q & A
What is the fundamental theorem of calculus and how does it relate to position, velocity, and acceleration?
-The fundamental theorem of calculus states that the integral from a to b of the derivative of a function, f'(x), is equal to the net change in the antiderivative of that function from a to b, which is f(b) - f(a). In terms of physics, this theorem can be applied to find the position by integrating velocity over time, where the change in position is equivalent to the definite integral of velocity.
What is the difference between distance and displacement?
-Distance is a scalar quantity that represents the total length of the path traveled by an object, regardless of direction. Displacement, on the other hand, is a vector quantity that represents the change in position from the starting point to the final position, taking into account direction.
How is speed defined in the context of this video?
-In the video, speed is defined as the absolute value of velocity. It is a scalar quantity that represents the rate at which an object covers distance along a straight line. When considering motion in two-dimensional space, speed remains the absolute value of velocity, but velocity itself becomes a vector.
How do you calculate the total distance traveled by an object?
-The total distance traveled by an object can be calculated by integrating the speed (absolute value of velocity) over the time interval of interest. This integral gives the total distance, similar to what an odometer would measure.
What is the process of finding the acceleration of an object at a specific time?
-To find the acceleration of an object at a specific time, you take the derivative of the velocity function with respect to time and then evaluate it at the given time. This process can be done using calculus or a graphing calculator.
How can you determine if an object is speeding up or slowing down?
-An object is speeding up if the velocity and acceleration have the same sign (both positive or both negative), and it is slowing down if the velocity and acceleration have opposite signs.
What is the significance of the integral of the absolute value of velocity in the context of this video?
-The integral of the absolute value of velocity gives the total distance traveled by an object over a given time interval. This is useful for understanding how far an object has moved, regardless of the direction of motion.
How do you find the position of a particle at a specific time using integration?
-To find the position of a particle at a specific time, you integrate the velocity function over the time interval from the initial time to the time of interest. The result is the change in position, which can be added to the initial position to find the final position.
What is the correct syntax for computing a definite integral on a TI-83 calculator?
-On a TI-83 calculator, you would use the 'math' menu, select '9' for definite integral, and then enter 'f int' followed by the function, the variable of integration (usually 'x'), and the lower and upper bounds of integration separated by commas.
How can you determine the time at which two particles are moving with the same velocity?
-To find the time at which two particles are moving with the same velocity, you set their velocity functions equal to each other and solve for the time variable. This can be done graphically by plotting both velocity functions and finding the intersection points, or algebraically by solving the equation.
What is the process for finding the first time a particle changes direction?
-To find the first time a particle changes direction, you need to determine when its velocity changes sign. This can be done by finding the zeros of the velocity function and identifying the first time instance where the velocity goes from positive to negative or vice versa.
Outlines
📚 Introduction to Distance, Displacement, and Calculus
The video begins with an introduction to the concepts of distance and displacement, linking them to the fundamental theorem of calculus. The instructor explains how the integral of velocity between two time points represents the change in position, or displacement. Speed is introduced as the absolute value of velocity, and the total distance traveled is defined as the integral of speed over time. The video also covers how to calculate definite integrals using a calculator, specifically for a TI-83 or TI-84, with an example of integrating a quadratic function.
🔍 Calculating Particle Motion with Calculus
This paragraph delves into a detailed example of a particle moving along the x-axis with a given velocity function. The instructor demonstrates how to find the acceleration by taking the derivative of the velocity function and how to determine the position of the particle at a specific time using a definite integral. The concept of total distance traveled is also explored, with the integral of the absolute value of velocity providing this measure. The paragraph concludes with a brief mention of an example problem from a 2018 calculus exam.
📈 Analyzing Particle Velocity and Position with Graphs
The instructor discusses how to determine when two particles are moving with the same velocity by comparing their velocity functions. The use of graphing to find the intersection of two velocity functions is introduced, along with the method of solving for the time when the velocities match. The paragraph also covers how to find when a particle is moving in a particular direction based on the sign of its velocity and how to determine when two particles are moving in the same direction by analyzing the signs of their velocities over time.
📘 Deriving Acceleration and Finding Direction Changes
In this section, the focus is on finding the acceleration of a particle and determining when it is speeding up or slowing down. The instructor uses the derivative of the velocity function to find acceleration and then examines the sign of the velocity and acceleration at a specific time to conclude the particle's motion state. Additionally, the process of finding the first time a particle changes direction by integrating its velocity from a known position is explained.
📝 Solving for Position and Distance with Definite Integrals
The paragraph presents an example from a 2016 calculus exam, where the position of a particle at time zero is found by integrating its velocity function from time zero to a given time and then adjusting for the known position at that later time. The total distance traveled by the particle over a specific time interval is also calculated using the integral of the absolute value of its velocity function, demonstrating the application of definite integrals in solving motion problems.
🔢 Concluding with Total Distance Calculation
The final paragraph wraps up the video with a summary of the key learning points, including the calculation of total distance traveled by a particle. The instructor reiterates the method of using the integral of the absolute value of velocity to find this distance, emphasizing the practicality of this approach in solving real-world motion problems.
Mindmap
Keywords
💡Distance
💡Displacement
💡Velocity
💡Acceleration
💡Position
💡Speed
💡Integral
💡Anti-derivative
💡Calculator
💡Free Response
💡Direction
Highlights
Introduction to the fundamental theorem of calculus and its application to position, velocity, and acceleration.
Explanation of how the integral of velocity between two time values equates to displacement.
Definition of speed as the absolute value of velocity, applicable in both one-dimensional and two-dimensional motion.
Total distance traveled is defined as the integral of speed between two time values, analogous to an odometer.
Guidance on how to compute definite integrals using a calculator, specifically for TI-83 and TI-84 models.
Example problem: Calculating the acceleration of a particle given its velocity function using a calculator.
Use of definite integrals to find the position of a particle at a specific time, given its velocity function.
Differentiation between distance traveled and displacement, with examples of calculating each.
Method to determine when two particles are moving with the same velocity by solving an equation.
Explanation of how to interpret the results of an integral to understand the motion of particles.
The importance of showing the equation solved using a calculator for clarity and accuracy in problem-solving.
Determination of when a particle is moving to the left by analyzing the sign of its velocity.
Analysis of when two particles are moving in the same direction by comparing their velocity signs.
Calculation of acceleration to determine if a particle is speeding up or slowing down at a specific time.
Finding the first time a particle changes direction by integrating its velocity from a starting point.
Example problem involving a particle's position and velocity, requiring the use of a calculator for integration.
Total distance traveled by a particle calculated over a specific time interval, using the integral of the absolute value of velocity.
Transcripts
Browse More Related Video
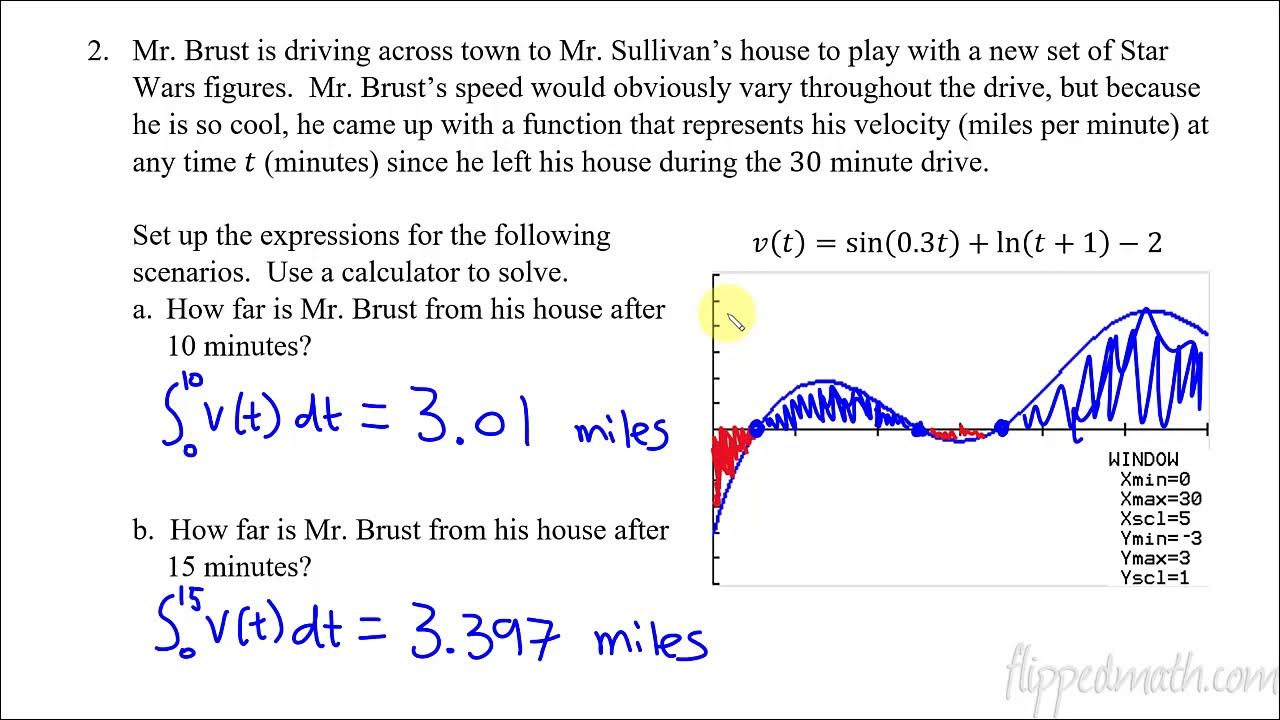
Calculus AB/BC – 8.2 Connecting Position, Velocity, and Acceleration of Functions Using Integrals

AP Calculus AB: Lesson 6.4 Rectilinear Motion

Distance vs. Displacement & Speed vs. Velocity | Kinematics Explained

AP Physics 1 review of 1D motion

Displacement and Velocity - How is it different from Distance and Speed? | Physics

Velocity and speed: Motion in One Dimension
5.0 / 5 (0 votes)
Thanks for rating: