Definition of a Limit
TLDRThis video introduces the concept of limits in calculus, focusing on the definition and notation of one-sided limits. It explains how limits exist when the left and right one-sided limits are equal and introduces common reasons for non-existence, such as disagreement between one-sided limits, unbounded behavior, and oscillation. The video also covers the linearity of limits, demonstrating how limits can be manipulated through addition, subtraction, and multiplication by constants. It concludes with a thought-provoking question about the preservation of limits under function transformations, encouraging further discussion and exploration.
Takeaways
- 📚 The video introduces the concept of limits, a fundamental topic in Calculus BC.
- 🔍 The value of a function at a specific point, like f(1), is determined by the height of the graph at that point, in this case, f(1) = 5.
- 📉 The one-sided limit, denoted as x approaching a value from the left or right, is an intuitive concept without a formal definition in this context.
- 🔄 The limit of a function as x approaches a value exists if the left and right one-sided limits are equal and the same real number.
- 🚫 A limit does not exist if the one-sided limits from the left and right are different, as demonstrated with the example of f(x) as x approaches 1.
- 📈 The video explains that a continuous function naturally has existing limits, whereas a jump discontinuity implies a non-existing limit.
- 📝 The process of finding the limit involves considering the behavior of the function as x approaches a certain value from both sides.
- 🤔 The video poses a question about the preservation of limit statements when a function is transformed, encouraging students to think about it.
- 📉 The example of a rational function, f(x) = (x - 5)(x + 4) / (x - 5), illustrates how to deal with factors that could potentially cancel out, leading to a hole in the graph.
- 📌 The graph of y = |x| / x is introduced, showing how the function behaves differently for positive x, negative x, and undefined at x = 0.
- 🚧 The video outlines reasons for limit non-existence, including disagreement of one-sided limits, unbounded behavior, and oscillation.
- 🔢 The linearity of limits property is presented, stating that the limit of a sum or a scaled function is the sum or scaled version of the individual limits.
Q & A
What is the definition of a limit in calculus?
-A limit in calculus is a value that a function approaches as the input (x) approaches a certain value. It is denoted as \( \lim_{x \to c} f(x) \), where \( c \) is the value that x is approaching, and \( f(x) \) is the function.
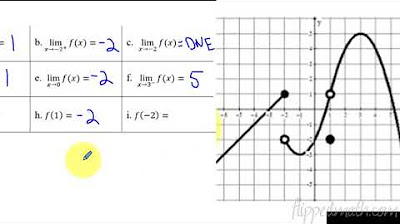
What is the value of f(1) in the given graph?
-In the provided graph, the value of f(1) is 5, as indicated by the filled in circle at x=1 on the graph.
What is the one-sided limit as x approaches 1 from the left?
-The one-sided limit as x approaches 1 from the left is 2, as the function values are getting closer to 2 as x approaches 1 from the negative side.
What is the one-sided limit as x approaches 1 from the right?
-The one-sided limit as x approaches 1 from the right is 5, as the function values are getting closer to 5 as x approaches 1 from the positive side.
Why does the limit as x approaches 1 not exist in the given graph?
-The limit as x approaches 1 does not exist because the one-sided limits from the left and the right are not equal. The left-hand limit is 2, and the right-hand limit is 5, which are different values.
What is the definition of a limit existing for a function?
-A limit exists for a function if the one-sided limits from the left and the right both exist and are equal. If they are the same number, denoted as \( l \), then the limit of \( f(x) \) as \( x \) approaches \( c \) is \( l \).
What is the value of f(4) in the given graph?
-In the provided graph, the value of f(4) is 1, as indicated by the filled in circle at x=4 on the graph.
What is the limit of f(x) as x approaches 4?
-The limit of f(x) as x approaches 4 is -2, as both the left-hand and right-hand limits approach -2.
Why does the limit as x approaches 7 not exist in the given graph?
-The limit as x approaches 7 does not exist because the one-sided limits from the left and the right are not equal. The left-hand limit is 0, and the right-hand limit is 4, which are different values.
What is the function f(x) in the given rational function example?
-The function f(x) in the rational function example is \( \frac{x - 5}{x + 4} \), which simplifies to \( x + 4 \) as long as \( x \neq -5 \).
What is the graph of y = |x| / x?
-The graph of y = \( |x| / x \) has a value of 1 for all positive x, a value of -1 for all negative x, and is undefined at x = 0, where open circles are placed on the graph.
What are the reasons for a limit not to exist?
-A limit may not exist due to one-sided limits disagreeing (jump discontinuity), unbounded behavior (approaching infinity), or oscillation (function wiggling back and forth without settling on a single value).
What is the linearity of limits in calculus?
-The linearity of limits states that if the limits of functions f and g are known, then the limit of a linear combination of these functions, such as \( a f(x) + b g(x) \), is equal to \( a \) times the limit of f plus \( b \) times the limit of g.
Outlines
📚 Introduction to Limits in Calculus
This paragraph introduces the concept of limits within the context of calculus, specifically for a calculus BC course. It explains the basic definition of a limit and uses the graph of a function to illustrate how to determine the value of a function at a specific point, denoted as 'f of one', which is given as five. The instructor then explores the idea of what happens to the function as the input 'x' approaches one from the left and right, introducing the concept of one-sided limits. The left-sided limit is two, while the right-sided limit is five, indicating a discontinuity at 'x equals one'. The paragraph concludes by defining a limit's existence when both one-sided limits exist and are equal.
🔍 Analyzing Function Values and Limits
The second paragraph delves deeper into the analysis of function values and limits. It begins by identifying the value of the function at 'f of 4' as one, based on the graph provided. It then discusses the limit of 'f of x' as 'x' approaches 4, highlighting that the one-sided limits from both sides are equal to negative two, thus the limit exists. In contrast, at 'x equals seven', the function exhibits a break in the graph, indicating a non-existence of the limit due to the disagreement of the one-sided limits. The paragraph also touches on rational functions, emphasizing the importance of factoring and understanding the implications of canceled factors, which can lead to holes in the graph or undefined function values.
📉 Understanding Limit Behaviors and Graphs
This paragraph focuses on the behavior of limits and graphing functions, particularly the function 'y equals absolute value of x divided by x'. It explains that for positive values of 'x', the function simplifies to one, while at 'x equals zero', the function is undefined, resulting in open circles on the graph. For negative values of 'x', the function yields negative one, as dividing a number by its negative counterpart results in a negative outcome. The paragraph also discusses reasons for the non-existence of limits, such as disagreement between one-sided limits, unbounded behavior leading to infinity, and oscillation, which prevents the function from approaching a singular value.
📘 Linearity of Limits and Transforming Functions
The final paragraph discusses the linearity property of limits, which is fundamental in calculus for proving theorems and solving problems. It explains that if the limits of functions 'f' and 'g' are known, the limit of their sum or difference is the sum or difference of their limits, and the same applies to multiplication by a constant. An example is provided to illustrate this concept, showing how to calculate the limit of a transformed function based on known limits. The paragraph concludes with a thought-provoking question about the preservation of limit statements when a function is transformed, inviting students to consider this concept and engage in further discussion.
Mindmap
Keywords
💡Limit
💡Function
💡One-sided Limit
💡Graph
💡Continuity
💡Discontinuity
💡Rational Function
💡Absolute Value
💡Unbounded Behavior
💡Oscillation
💡Linearity of Limits
Highlights
Introduction to limits in calculus BC.
Definition of a limit and its significance in understanding functions.
Explanation of the value of f(1) as seen on a graph.
Discussion on the one-sided limit as x approaches one from the left.
Illustration of the difference between approaching a value from the left and the right.
Definition of a limit existing when one-sided limits are equal.
Visual demonstration of the limit concept using a graph.
Explanation of a function's value at a specific point, f(4).
Analysis of the limit of f(x) as x approaches 4, illustrating one-sided limits.
Introduction to rational functions and their role in calculus.
Graphical representation of y = absolute value(x) / x.
Discussion on reasons for limit non-existence, such as one-sided limits disagreeing.
Explanation of unbounded behavior as a reason for limit non-existence.
Introduction to the concept of oscillation and its impact on limit existence.
Linearity of limits and its application in calculus.
Example of using linearity of limits to find the limit of a function.
Question posed on the preservation of limit statements through function transformations.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: