Divergence and Curl (Vector Fields)

Houston Math Prep
7 May 202013:11
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video delves into the concepts of vector fields, focusing on divergence and curl. It begins with a review of the gradient, explaining how it represents the direction of greatest increase for a scalar function. The script then introduces divergence, which measures the spreading of a vector field, and curl, which indicates the rotation of a vector field. Through examples, it illustrates how to calculate these operations in two and three dimensions, emphasizing the importance of understanding the type of object (scalar or vector) each operation yields.

Takeaways
  • 📚 The gradient of a scalar function is represented by del F and provides the direction of greatest increase of the function.
  • 🔍 The gradient operation involves taking partial derivatives with respect to each variable and assigning them to the components of a vector field.
  • 📈 The gradient is calculated for a function of x and y as ∂F/∂x, ∂F/∂y, and for a three-dimensional function as ∂F/∂x, ∂F/∂y, ∂F/∂z.
  • 🌀 The divergence of a vector field, denoted as div F or del dot F, measures how much the vector field is spreading out at a point and is calculated using partial derivatives.
  • 📉 Divergence in two dimensions is given by ∂M/∂x + ∂N/∂y, and in three dimensions by ∂M/∂x + ∂N/∂y + ∂P/∂z, where M, N, and P are the components of the vector field.
  • 🌐 The divergence theorem relates the flux through a surface to the integral of the divergence over a volume.
  • 🔄 The curl of a vector field, represented as del cross F, indicates the rotation or circulation of the field around a point and is calculated using a cross product in three dimensions.
  • 🔢 The curl operation results in a vector field, providing information about the field's rotation in the form of another vector field.
  • 📝 The script provides examples of calculating the gradient, divergence, and curl for both two and three-dimensional functions.
  • 🧭 Understanding the type of operation and the expected output (scalar or vector field) is crucial for correctly applying these multivariable calculus concepts.
Q & A

  • What is the gradient of a scalar function?

    -The gradient of a scalar function is a vector operation denoted as del F or ∇F, which involves taking the partial derivatives with respect to each variable and assigning them as the components of a vector field, indicating the direction of the greatest increase of the scalar function.

  • How is the gradient calculated for a function of two variables?

    -For a function of two variables, the gradient is calculated by taking the partial derivative with respect to x (∂f/∂x) and the partial derivative with respect to y (∂f/∂y), and these values become the first and second components of the resulting vector field.

  • What does the gradient represent in three-dimensional space?

    -In three-dimensional space, the gradient includes an additional term, the partial derivative with respect to z (∂f/∂z), and it represents a vector field with three components, indicating the direction of the greatest increase of the scalar function in 3D.

  • Can you provide an example of calculating the gradient for a given scalar function?

    -Sure, for the scalar function f(x, y) = x^2y + 2x, the gradient is calculated as ∇f = (∂f/∂x, ∂f/∂y) = (2xy + 2, x^2).

  • What is the divergence of a vector field?

    -The divergence of a vector field, denoted as div F or ∇ · F, is a scalar operation that measures how much a vector field is spreading out or converging at a point, and it is calculated as the sum of the partial derivatives of the vector field's components.

  • How is the divergence calculated for a two-dimensional vector field?

    -For a two-dimensional vector field F = (M, N), the divergence is calculated as div F = ∇ · F = (∂M/∂x) + (∂N/∂y).

  • What does a positive divergence indicate about a vector field?

    -A positive divergence indicates that the vector field is spreading out or diverging from a point, suggesting a source or a region of positive flux.

  • Can you give an example of calculating the divergence for a three-dimensional vector field?

    -For a three-dimensional vector field F = (M, N, P), the divergence is calculated as div F = ∇ · F = (∂M/∂x) + (∂N/∂y) + (∂P/∂z).

  • What is the curl of a vector field?

    -The curl of a vector field, denoted as curl F or ∇ × F, is a vector operation that measures the rotation or circulation of the vector field around a point, and it is calculated using the cross product of the del operator with the vector field.

  • How is the curl calculated for a three-dimensional vector field?

    -For a three-dimensional vector field F = (M, N, P), the curl is calculated using the determinant of a matrix with the unit vectors i, j, k in the first row, the partial derivatives of the components in the second row, and the components of the vector field in the third row.

  • What does a zero curl indicate about a vector field?

    -A zero curl indicates that there is no rotation or circulation of the vector field around a point, suggesting that the field could be the gradient of a scalar potential function.

  • How can one remember the type of object resulting from gradient, divergence, and curl operations?

    -The gradient of a scalar function results in a vector field, the divergence of a vector field results in a scalar function, and the curl of a vector field results in another vector field. Understanding the input and output objects of these operations is crucial for correctly applying them in multivariable calculus.

Outlines
00:00
📚 Introduction to Vector Fields and Gradient

This paragraph introduces the concept of vector fields and the gradient operation. It explains that the gradient of a scalar function, denoted as del F, involves taking partial derivatives with respect to x and y (and z in 3D space), which results in a vector field indicating the direction of greatest increase. The paragraph provides examples of calculating the gradient for functions of two and three variables, emphasizing the gradient's role in determining the direction of steepest ascent.

05:00
🌀 Understanding Divergence and Its Calculation

The second paragraph delves into the concept of divergence, denoted as div F or del dot F, which measures how much a vector field is spreading out at a point. It is calculated by taking the dot product of the del operator, represented by partial derivatives, with a vector field. The paragraph includes examples of calculating divergence in both two and three dimensions, highlighting the scalar output that indicates the degree of spreading or contraction of the vector field.

10:01
🔍 Exploring the Curl Operation and Its Significance

The final paragraph discusses the curl operation, represented as del cross F, which is used to determine the rotation or circulation of a vector field around a point. The curl is calculated using a cross product in three-dimensional space, resulting in a vector field that represents the circulation density. The paragraph provides examples of calculating the curl for both two and three-dimensional vector fields, emphasizing the importance of understanding the type of object being operated on and the expected output.

Mindmap
Keywords
💡Vector Field
A vector field is a concept in physics and mathematics that assigns a vector to every point in space. In the context of the video, vector fields are used to describe the direction and magnitude of quantities such as force or velocity at different points. The script discusses how to calculate the gradient, divergence, and curl of vector fields, which are fundamental operations in vector calculus.
💡Gradient
The gradient is a vector operation that represents the direction and rate of the fastest increase of a scalar function. In the video, the gradient is introduced as a way to determine the direction of greatest increase for a given scalar function, such as temperature or pressure, and is illustrated with examples involving partial derivatives with respect to x, y, and z.
💡Divergence
Divergence is a measure of how a vector field is spreading out or converging at a given point. It is calculated using the dot product of the del operator with the vector field. The video explains that divergence can be thought of as the flux through a surface and is related to the concept of spreading or 'diverging' of a field, as shown in the examples with 2D and 3D vector fields.
💡Curl
Curl is a vector operation that describes the rotation or circulation of a vector field around a point. It is calculated using the cross product of the del operator with the vector field. The video script uses the curl to illustrate how to determine the rotational aspect of a field, with examples that include the calculation of curl for both 2D and 3D vector fields.
💡Scalar Function
A scalar function is a mathematical function that maps each point in space to a single number, as opposed to a vector function which maps to a vector. In the video, scalar functions are used to demonstrate the calculation of the gradient, which is a vector field derived from the partial derivatives of the scalar function.
💡Partial Derivative
A partial derivative is the derivative of a function with respect to one of its variables, while the other variables are held constant. The video script discusses the process of taking partial derivatives as part of the gradient calculation for scalar functions of multiple variables.
💡Dot Product
The dot product is an algebraic operation that takes two equal-length sequences of numbers (usually coordinate vectors) and returns a single number. In the context of the video, the dot product is used to calculate the divergence of a vector field, which involves summing the products of corresponding components.
💡Cross Product
The cross product is a binary operation on two vectors in three-dimensional space, resulting in a vector that is perpendicular to the plane containing the two original vectors. The video explains how the cross product is used to calculate the curl of a vector field, which provides information about the field's rotation.
💡Del Operator
The del operator, often represented by the symbol '∇', is a vector differential operator used in vector calculus. In the video, the del operator is used in the context of calculating the gradient, divergence, and curl, where it represents the vector of partial derivatives with respect to spatial coordinates.
💡Flux
Flux is a concept in physics that refers to the rate of flow of a fluid through a surface, or in the context of the video, the rate at which a vector field is spreading out through a surface. The divergence of a vector field is related to the flux through a surface, as discussed in the video's explanation of the divergence theorem.
💡Chain Rule
The chain rule is a fundamental principle in calculus for finding the derivative of a composite function. In the video, the chain rule is mentioned in the context of calculating partial derivatives for the gradient of a function of multiple variables, particularly when dealing with exponential functions.
Highlights

Introduction to vector fields, divergence, and curl in the context of multivariable calculus.

Review of the gradient as an operation that takes a scalar function and outputs a vector field indicating the direction of greatest increase.

Explanation of the gradient calculation for a scalar function of two variables, resulting in a vector field.

Demonstration of gradient calculation for a scalar function in three-dimensional space involving partial derivatives with respect to X, Y, and Z.

Clarification that the gradient of a scalar function results in a vector field, not just a single vector.

Introduction to divergence as a measure of how much a vector field is spreading out at a point, expressed as div F or del dot F.

Methodology for calculating divergence in two dimensions using partial derivatives with respect to X and Y.

Extension of divergence calculation to three dimensions, including the partial derivative with respect to Z.

Divergence's role in determining the flux through a surface and its relation to the divergence theorem.

Illustration of divergence calculation for a two-dimensional vector field, highlighting the effect of the X value on spreading out.

Example of divergence in a three-dimensional vector field, showing a constant positive divergence indicating spreading out at all points.

Transition to the concept of curl, described as del cross F, which measures the rotation of a vector field around a point.

Elucidation of curl calculation in two dimensions, emphasizing the use of the special unit vector k hat.

Detailed curl calculation for a three-dimensional vector field using the determinant method and cross product.

Differentiation between scalar and vector outputs in operations, stressing the importance of understanding the type of object being dealt with.

Emphasis on the importance of knowing the type of operation and expected output object in multivariable calculus problems.

Conclusion summarizing the significance of understanding vector fields, divergence, curl, and their practical applications in calculus.

Transcripts

Browse More Related Video

Vector Fields, Divergence, and Curl

Calculus 3 Lecture 15.2: How to Find Divergence and Curl of Vector Fields

Curl 3 | Partial derivatives, gradient, divergence, curl | Multivariable Calculus | Khan Academy

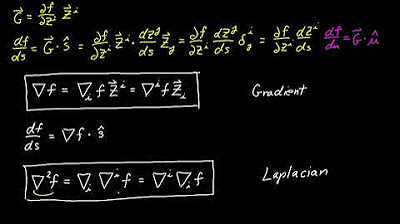
Video 39 - Gradient

Divergence 1 | Multivariable Calculus | Khan Academy

3d curl intuition, part 1

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Vector FieldsDivergenceCurlGradientMultivariable CalculusScalar FunctionPartial DerivativeDot ProductCross ProductMathematics EducationVector Analysis