Derivatives and Tangent Vectors (Vector-Valued Functions)
TLDRThis video from Houston Math Prep delves into the concept of derivatives and tangent vectors for vector-valued functions. It explains the process of differentiating each component of a vector function independently, using standard calculus rules, and introduces various differentiation rules applicable to vector functions. The video provides examples to illustrate the calculation of derivatives, finding tangent vectors at specific points, and determining instantaneous velocity and speed. It sets the stage for further exploration into unit tangent vectors and principal unit normal vectors in upcoming videos.
Takeaways
- 📚 The video introduces the concept of derivatives and tangent vectors for vector-valued functions, emphasizing the importance of understanding the limit definition from single variable calculus.
- 📉 The process of finding derivatives in vector-valued functions involves evaluating the derivative of each component independently, using standard differentiation rules.
- 🔍 The video explains that the derivative of a vector-valued function is a vector itself, pointing in the direction of the tangent to the curve at a specific point.
- 📈 Derivative rules for vector-valued functions, such as scalar multiple, sum and difference, and the chain rule, are analogous to those for scalar functions.
- 📚 The video discusses three types of products (scalar, dot, and cross) and their differentiation, noting that the dot product results in a scalar function, while the others yield vectors.
- 📝 An example is provided to illustrate the process of differentiating a vector-valued function, showing the calculation of derivatives for each component.
- 📍 The concept of tangent vectors is explained, showing how to find them by differentiating the vector-valued function and then substituting a specific value for 't'.
- 🚀 An example demonstrates finding the tangent vector at a specific point on a vector-valued function, using the derivatives of the function's components.
- 🏃♂️ The video explains how to calculate instantaneous velocity and speed of a particle moving along a vector-valued path, using the derivative of the position function.
- 🔢 The magnitude of the velocity vector at a given time 't' gives the speed of the particle, which is found by taking the square root of the sum of the squared components of the velocity vector.
- 🔄 The video concludes with a mention of using second derivatives to find acceleration vectors, hinting at the content of the next video in the series.
Q & A
What is the main topic of the video?
-The main topic of the video is finding derivatives and tangent vectors for vector-valued functions.
How does the concept of a secant line relate to the derivative of a vector-valued function?
-The concept of a secant line in single-variable calculus is similar to the derivative of a vector-valued function. As two points on a function are brought closer together, the secant line approaches a tangent line. In vector-valued functions, a vector between two points on the curve approaches a single point, becoming a tangent vector that points straight forward in time at that exact moment on the curve.
How is the derivative of a vector-valued function calculated?
-The derivative of a vector-valued function is calculated by evaluating the derivative of each component of the vector-valued function independently, using the standard rules of differentiation for scalar functions.
What are the three types of products mentioned in the context of vector-valued functions?
-The three types of products mentioned are scalar product, dot product, and cross product, all of which follow the product rule from single-variable calculus but yield different types of results.
What is the result of a dot product derivative in the context of vector-valued functions?
-The result of a dot product derivative in the context of vector-valued functions is a scalar function, not a vector.
What is the purpose of finding the derivative of a vector-valued function with respect to time 't'?
-The derivative of a vector-valued function with respect to time 't' gives the rate of change of the function at any given point, which can be used to find tangent vectors, instantaneous velocity, and other related quantities.
How do you find the instantaneous velocity of a particle moving along a vector-valued function?
-The instantaneous velocity of a particle moving along a vector-valued function is found by taking the derivative of the position function (the vector-valued function) with respect to time, resulting in a velocity vector.
What is the formula for the magnitude of the velocity vector, which represents the speed of the particle?
-The magnitude of the velocity vector, which represents the speed of the particle, is calculated as the square root of the sum of the squares of its components.
How can you find the tangent vector at a specific point on a vector-valued function?
-To find the tangent vector at a specific point on a vector-valued function, you differentiate the function to find the derivative (tangent vector function) and then evaluate this derivative at the specific value of 't' for which you want the tangent vector.
What is the significance of finding the second derivative of a vector-valued function?
-The second derivative of a vector-valued function can be used to find the acceleration vector, which provides information about the rate of change of velocity and can be used to analyze the motion of objects in more detail.
Outlines
📚 Introduction to Derivatives of Vector-Valued Functions
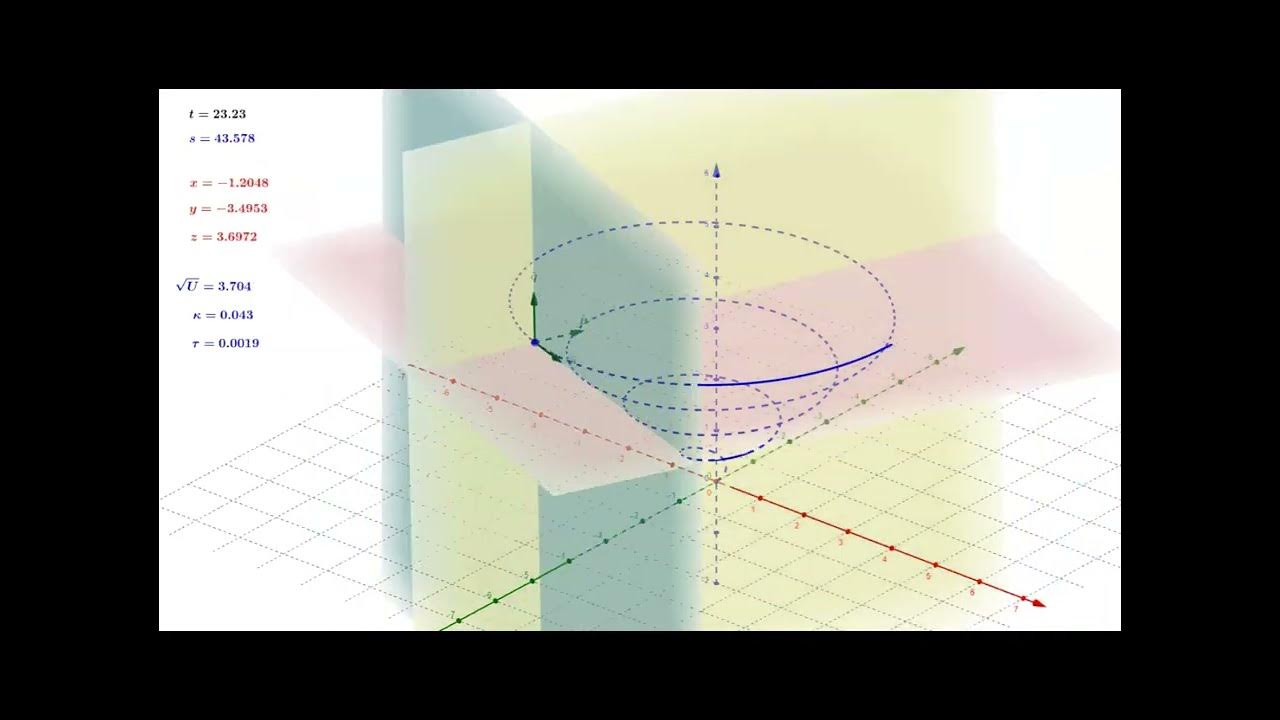
This paragraph introduces the concept of finding derivatives and tangent vectors for vector-valued functions. It starts with a brief mention of the limit definition of the derivative, which is not the focus of the video. The main idea is to differentiate each component of the vector-valued function independently, using standard differentiation rules, as each component is a scalar function. The paragraph also introduces various differentiation rules applicable to vector-valued functions, such as the scalar multiple rule, sum and difference rule, and the chain rule. It emphasizes the importance of correctly identifying the type of object (vector or scalar) resulting from the application of these rules, especially when dealing with scalar, dot, and cross products. The paragraph concludes with an example of finding the derivative of a given vector-valued function, which involves applying the chain rule and product rule, and then writing the solution in vector form.
🔍 Calculating Tangent Vectors and Instantaneous Velocity
This paragraph delves into the application of derivatives to find tangent vectors at specific points on a vector-valued function, akin to finding tangent lines in scalar calculus. It provides a step-by-step example of how to differentiate a given vector-valued function and then evaluate the derivative at a particular value of t to obtain the tangent vector at that point. The example involves differentiating components such as cosine and sine functions and then plugging in the specific t-value to get the tangent vector. The paragraph also discusses the concept of instantaneous velocity, which is the derivative of the position function of a particle, and provides an example of finding the instantaneous velocity at a given time t. It concludes with an example of calculating the speed of the particle at a specific time by finding the magnitude of the velocity vector.
🚀 Derivatives for Acceleration and Upcoming Topics
The final paragraph briefly touches on the use of second derivatives to find acceleration vectors, which is a topic for the next video in the series. It also mentions the upcoming discussion on unit tangent vectors and principal unit normal vectors, indicating the continuation of the series. The paragraph wraps up with a thanks to the viewers and an anticipation for the next video, creating a smooth transition to further topics in the study of vector calculus.
Mindmap
Keywords
💡Derivative
💡Vector-Valued Function
💡Tangent Vector
💡Limit Definition
💡Scalar Function
💡Chain Rule
💡Product Rule
💡Scalar Multiple Rule
💡Sum and Difference Rule
💡Instantaneous Velocity
💡Speed
Highlights
Introduction to finding derivatives and tangent vectors for vector-valued functions.
Explanation of the limit definition of the derivative of a vector-valued function.
Discussion on the concept of secant and tangent lines in the context of vector-valued functions.
Differentiation of vector-valued functions by evaluating the derivative of each component independently.
Recollection of derivative rules from single variable calculus and their application to vector-valued functions.
Introduction of scalar multiple rule for differentiating vector-valued functions.
Explanation of the sum and difference rule for differentiating vector addition or subtraction.
Application of the chain rule in vector-valued functions when substituting scalar functions.
Differentiation of scalar, dot, and cross products in vector-valued functions following the product rule.
Emphasis on the importance of obtaining the correct type of object (scalar or vector) after differentiation.
Example calculation of the derivative of a vector-valued function involving exponential and trigonometric functions.
Derivation of the formula for a vector tangent to the curve at any given t value.
Method to find a tangent vector at a specific t value by differentiating and plugging in the value.
Example of finding a tangent vector to a function at t equals pi over four.
Instantaneous velocity and speed calculation for a particle moving along a vector-valued function.
Derivation of the velocity function and its evaluation at a specific time to find instantaneous velocity.
Calculation of speed as the magnitude of the velocity vector at a given time.
Introduction to finding acceleration vectors using second derivatives.
Anticipation of the next video in the series on unit tangent vectors and principal unit normal vectors.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: