Torsion: How curves twist in space, and the TNB or Frenet Frame
TLDRThis video script delves into the geometric concepts of curves in space, focusing on three key vectors: the tangent, normal, and binormal. It explains how the tangent vector indicates direction, the normal captures the tangent's rate of change, and the binormal is the cross product of the tangent and normal, pointing perpendicular to the curve's plane. The script further explores the implications of the derivative of the binormal vector, revealing torsion as a measure of the twisting of the curve's plane in space. The concepts of curvature and torsion are compared, with curvature describing the in-plane bending and torsion indicating the out-of-plane twisting of the curve.
Takeaways
- 📐 The tangent vector (T) is the derivative of the position vector with respect to the arc length parameter and represents the direction of motion along the curve.
- 🔍 The normal vector (N) is the derivative of the tangent vector with respect to the parameter and captures how the tangent vector is changing, pointing towards the center of a circle in the example given.
- 🌀 The binormal vector (B) is defined as the cross product of the tangent and normal vectors, and it is perpendicular to both, pointing straight up in the case of a circle.
- 🔄 The change in the binormal vector with respect to the arc length parameter (dB/ds) is used to understand the twisting of the plane defined by the tangent and normal vectors.
- 📉 The curvature (kappa) is related to the change in the tangent vector and is a measure of how much the curve bends within the plane defined by the tangent and normal vectors.
- 🌀 Torsion (tau) is the negative of the dot product between the derivative of the binormal vector and the normal vector, indicating the degree of twisting of the curve's plane in space.
- 🔄 A zero torsion value implies no twisting of the plane, as seen in the example of a circle where the binormal vector remains constant.
- 🔧 Large torsion values indicate rapid twisting of the curve's plane, while small values suggest slow or minimal twisting.
- 📚 The concepts of curvature and torsion are distinct, with curvature describing the in-plane bending of the curve and torsion describing the out-of-plane twisting.
- 📈 The computation of torsion involves understanding the orientation and orthogonality of the derivative of the binormal vector in relation to the tangent and binormal vectors.
- 🎥 The video script uses visual examples to illustrate the concepts of tangent, normal, and binormal vectors, as well as curvature and torsion, to aid in understanding these multivariable calculus topics.
Q & A
What is the tangent vector in the context of a curve in space?
-The tangent vector is the derivative of the position vector with respect to the arc length parameter 's'. It represents the direction in which the curve is moving at any given point.
How is the normal vector related to the tangent vector?
-The normal vector is the derivative of the tangent vector with respect to the parameter 's'. It captures the rate and direction of change of the tangent vector, indicating how the curve is bending.
What does the binormal vector represent in the context of a curve?
-The binormal vector is the cross product of the tangent and normal vectors. It is perpendicular to both the tangent and normal vectors, representing the 'twisting' of the curve in three-dimensional space.
Why is the binormal vector always pointing upwards in the example of a circle?
-In the case of a circle, the tangent and normal vectors lie in a single plane, and since the cross product of two vectors in the same plane results in a vector perpendicular to that plane, the binormal vector points straight up.
What does the change in the binormal vector with respect to 's' indicate?
-The change in the binormal vector with respect to 's', denoted as dB/ds, indicates the rate and direction of the 'twisting' of the curve's tangent plane in space.
How is the curvature of a curve related to the tangent and normal vectors?
-Curvature, denoted by the parameter kappa, is the magnitude of the rate of change of the tangent vector with respect to the arc length 's'. It describes how sharply the curve is bending within the tangent plane.
What is torsion, and how is it different from curvature?
-Torsion is a measure of how much the tangent plane itself is twisting in space as one moves along the curve. It is different from curvature, which describes the rate of change of the tangent vector within the tangent plane.
What is the relationship between dB/ds and the normal vector?
-The derivative of the binormal vector with respect to 's', dB/ds, is parallel to the normal vector, indicating that the rate of change of the binormal vector is in the direction of the normal vector.
How is torsion mathematically defined in terms of dB/ds and the normal vector?
-Torsion, denoted by tau, is defined as the negative of the dot product between dB/ds and the normal vector. It is a scalar value that quantifies the twisting of the tangent plane.
Why is the torsion zero in the example of a circle?
-In the case of a circle, the tangent plane does not twist as one moves along the curve, resulting in a constant binormal vector and thus a torsion of zero.
What can we infer from a large torsion value compared to a small one?
-A large torsion value indicates that the tangent plane is twisting rapidly as one moves along the curve, while a small torsion value suggests a slower or minimal twisting of the tangent plane.
Outlines
📐 Understanding Curve Motion with Tangent, Normal, and Binormal Vectors
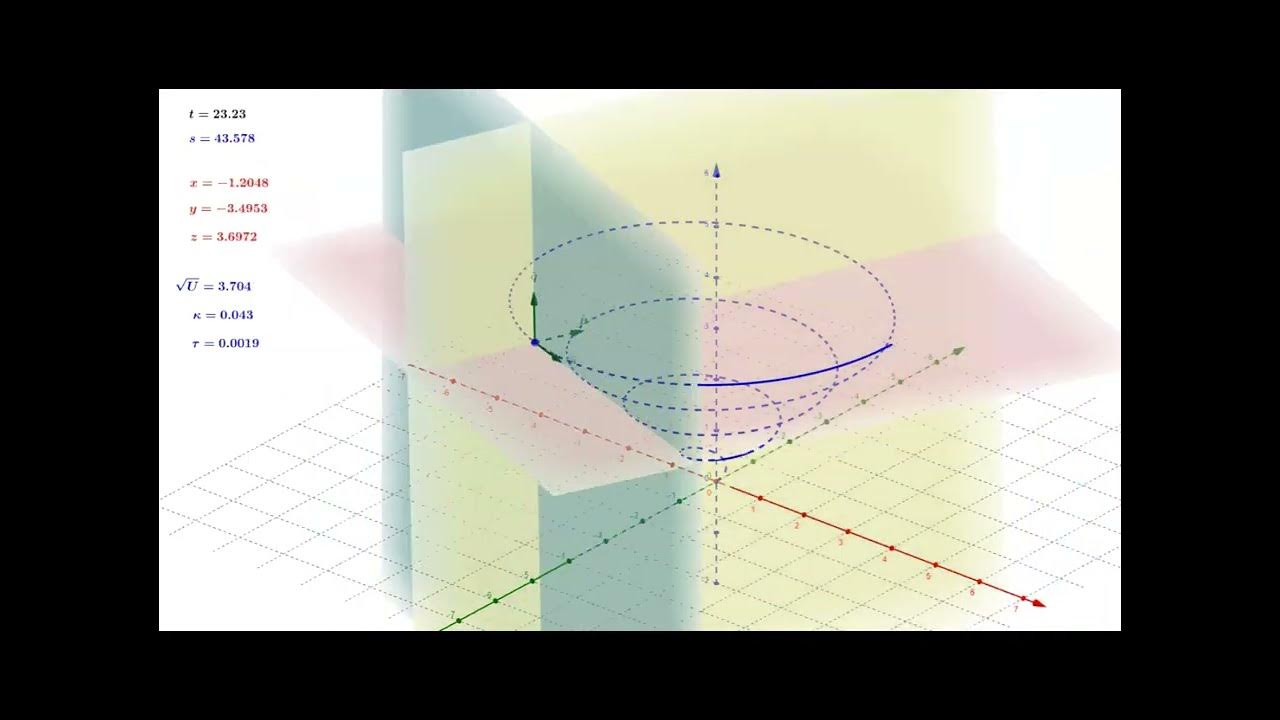
This paragraph introduces the concept of describing motion along a curve in space using three fundamental vectors: the tangent, normal, and binormal vectors. The tangent vector, derived from the derivative of the position vector with respect to arc length, indicates the direction of motion at any given point on the curve. The normal vector, which is the derivative of the tangent vector, captures the rate of change of the tangent vector, and in the case of a circle, points towards the center. The binormal vector, a cross product of the tangent and normal vectors, is perpendicular to both and, for a circle, points straight up. The paragraph also discusses the implications of these vectors in more complex, three-dimensional curves, where the plane defined by the tangent and normal vectors can twist, and the binormal vector changes accordingly to reflect this twisting motion.
🔍 Deep Dive into Torsion: The Rate of Twisting of the Tangent-Normal Plane
This section delves into the mathematical computation of torsion, which is the rate at which the plane defined by the tangent and normal vectors twists as it moves along the curve. The derivative of the binormal vector with respect to the arc length parameter is shown to be orthogonal to both the tangent and binormal vectors, indicating that it must be parallel to the normal vector. The torsion, represented by the scalar τ, is defined as the negative dot product between this derivative and the normal vector. The concept is illustrated with two examples: a circle, where the torsion is zero because the binormal vector does not change, and a more complex three-dimensional curve, where the torsion indicates the degree of twisting of the tangent-normal plane. The paragraph concludes by emphasizing the difference between curvature, which describes the rate of change of the tangent vector within the plane, and torsion, which describes the twisting of the plane itself.
🌐 Visualizing Curvature and Torsion in Curved Motion
The final paragraph wraps up the discussion by contrasting curvature and torsion, two distinct measures that describe different aspects of motion along a curve. Curvature refers to the rate at which the tangent vector changes within the tangent-normal plane, indicating how sharply the curve is bending in that plane. Torsion, on the other hand, measures the rate at which the tangent-normal plane twists in space as the curve progresses. The paragraph encourages viewers to engage with the content by asking questions, appreciating the mathematical exploration, and suggests further learning through a playlist of multivariable calculus videos for those interested in deepening their understanding of these concepts.
Mindmap
Keywords
💡Tangent Vector
💡Normal Vector
💡Binormal Vector
💡Curvature
💡Torsion
💡Cross Product
💡Arc Length Parameter
💡Derivative
💡Unit Vector
💡Dot Product
💡Plane
Highlights
Introduction to the three fundamental vectors that describe motion along a curve: the tangent, normal, and binormal vectors.
Explanation of the tangent vector as the derivative of the position vector with respect to the arc length parameter.
Description of the tangent vector's role in indicating the direction of motion along a curve.
Introduction of the normal vector as the derivative of the tangent vector with respect to the parameter.
Illustration of the normal vector's function in capturing changes in the tangent vector's direction.
Definition of the binormal vector as the cross product of the tangent and normal vectors.
Clarification that the binormal vector is perpendicular to both the tangent and normal vectors, pointing 'straight up' in the case of a circle.
Discussion of the binormal vector's behavior in three-dimensional space and its relation to the curve's twisting motion.
Computational approach to understanding the change in the binormal vector with respect to the arc length parameter.
Use of the cross product rule to derive the expression for the derivative of the binormal vector.
Identification of the derivative of the binormal vector as orthogonal to both the tangent and binormal vectors.
Introduction of the torsion, tau, as a measure of the twisting of the plane defined by the tangent and normal vectors.
Derivation of the formula for torsion, showing it as the negative dot product between the derivative of the binormal vector and the normal vector.
Visual examples demonstrating the concept of torsion in both two-dimensional and three-dimensional curves.
Comparison between curvature and torsion, explaining their distinct roles in describing a curve's motion.
Practical implications of understanding curvature and torsion in the study of multivariable calculus.
Invitation for viewers to engage with the content through comments and likes, fostering a community of mathematicians.
Promotion of a playlist of multivariable calculus videos for further exploration of the topic.
Transcripts
Browse More Related Video
Video 91 - Frenet Formulas

Calculus 3: Arc Length and Curvature (Video #9) | Math with Professor V

Calculus 3 Lecture 12.3: Arc Length/Parameterization, TNB (Frenet-Serret) Intro

Video 76 - Curvature Basics

Partial derivative of a parametric surface, part 1

Normal Vectors and Equations of Planes (Calculus 3)
5.0 / 5 (0 votes)
Thanks for rating: