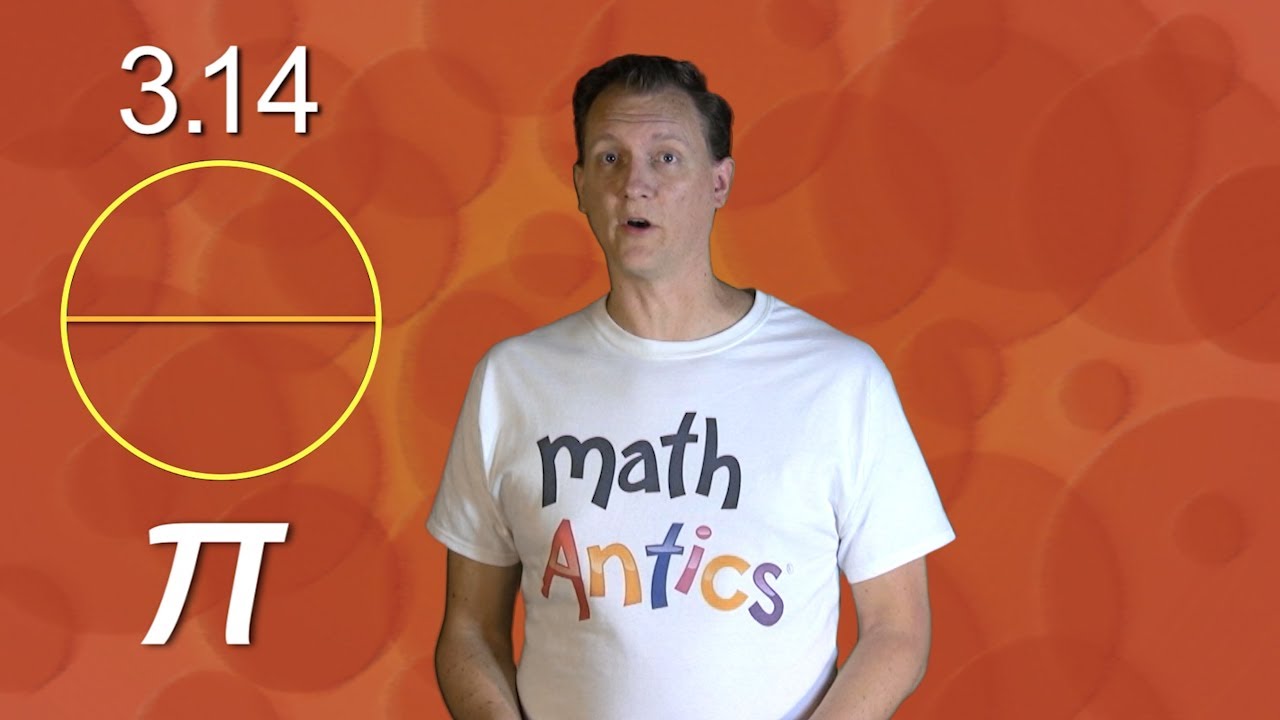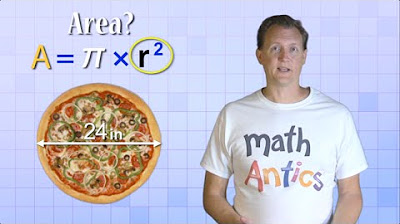Unveiling The Remarkable Discovery Of Pi By A Genius - Prepare To Be Amazed!
TLDRThis video script narrates an engaging journey to understand the value of pi, traditionally approximated as 3.14. The host creatively uses a cereal box and simple tools to replicate Archimedes' method of discovering pi by rolling a wheel along a straight edge. By marking the wheel's path and comparing it to the diameter, the video demonstrates how pi is derived from the number of diameters it takes for a wheel to complete one rotation. The script also includes a brief explanation of the formula for circumference, using the radius and pi, and concludes with an encouragement to practice drawing and subscribe for more educational content.
Takeaways
- 📚 Pi, approximately equal to 3.14, is a mathematical constant representing the ratio of a circle's circumference to its diameter.
- 👨🏫 Archimedes is credited with being the first to calculate an approximation of pi, using methods that were not sophisticated by modern standards.
- 🛠️ The video demonstrates a creative way to understand pi using everyday items like a cardboard box and cereal, instead of advanced tools.
- 🔪 The cardboard is cut to create a 'road' on which a wheel can roll, simulating the path of the circumference of a circle.
- 📏 A wheel is constructed from cardboard, marking the center as the axle and drawing the circumference to represent a circle.
- 🎨 The wheel is detailed with a marker to give it a more realistic wooden appearance, enhancing the visual demonstration.
- 🚂 The wheel is rolled along the cardboard 'road' to visually determine the length of the circumference relative to the diameter.
- 📐 The experiment shows that it takes approximately 3.14 diameters for the wheel to complete one full cycle, thus deriving the value of pi.
- 📝 The video explains the formula for the circumference of a circle, C = 2πr, and demonstrates how to use it with a given radius.
- 🔢 An example calculation is performed using the measured radius to estimate the circumference, aligning with the value obtained through the wheel rolling demonstration.
- 📖 The presenter mentions a book they wrote about Archimedes, highlighting his genius and contributions to mathematics and science.
Q & A
Why is the number pi approximately equal to 3.14?
-Pi is approximately equal to 3.14 because Archimedes discovered that the circumference of a circle is about 3.14 times the diameter, which is a simplified way to express the ratio of the circumference to the diameter.
Who first worked out the approximate value of pi?
-Archimedes of Syracuse is credited with being the first to calculate an approximation of pi, using the method of inscribing and circumscribing polygons around a circle.
What did Archimedes use to approximate the value of pi?
-Archimedes used a method involving polygons inscribed and circumscribed around a circle to approximate the value of pi, without the sophisticated tools available today.
What is the relationship between the circumference and the diameter of a circle according to the script?
-The script explains that the circumference of a circle is approximately 3.14 times the diameter, which is the fundamental definition of pi.
How did the script demonstrate the approximation of pi using a cardboard wheel?
-The script demonstrated the approximation of pi by creating a cardboard wheel and rolling it along a straight line, marking the distance it traveled, which corresponds to the circumference, and comparing it to the diameter.
What materials were used in the script to demonstrate the concept of pi?
-The materials used in the script included a cardboard from a cereal box, glue, a sharpie pen, and a compass or round object to draw the circle.
What is the significance of the sharpie pen in the demonstration?
-The sharpie pen was used to draw the circle, mark the axle, and add details to the cardboard wheel to make it resemble an actual wheel, as well as to highlight the circumference for visibility during the demonstration.
How does the script relate the ancient method of Archimedes to a modern understanding of pi?
-The script relates the ancient method by showing a hands-on demonstration using simple materials, which helps to visualize how Archimedes might have approximated pi and connects it to the modern mathematical constant we use today.
What is the formula for the circumference of a circle in terms of pi?
-The formula for the circumference of a circle in terms of pi is C = 2 * pi * r, where C is the circumference, pi is approximately 3.14, and r is the radius of the circle.
How did the script use the cardboard wheel to show that the circumference is about 3.14 times the diameter?
-The script rolled the cardboard wheel along a straight line and marked the distance it traveled, which is the circumference. By comparing this distance to the diameter of the wheel, it showed that the circumference is approximately 3.14 times the diameter.
What is the purpose of the subscribe button and bell mentioned in the script?
-The subscribe button and bell are there to encourage viewers to subscribe to the channel and to enable notifications for new video uploads, thus keeping the audience engaged and informed.
Outlines
🔍 Discovering Pi: The Origin Story
Archimedes discovered the value of Pi (3.14) by measuring the circumference of a circle relative to its diameter. Despite lacking sophisticated tools, he used a wooden cartwheel to experiment and make his calculations. This hands-on approach involved measuring and cutting cardboard to simulate the wheel and road, demonstrating the process visually.
🔢 Calculating Circumference with Pi
Archimedes' experiment is further detailed as he marks the wheel's circumference, showing it equates to 3.14 times the diameter, hence Pi. The relationship is verified using a modern calculator and measuring tools, proving the formula 2πr for the circumference. This section explains the practical steps and measurements involved, reinforcing the concept of Pi's value and its real-world application.
Mindmap
Keywords
💡Pi
💡Archimedes
💡Circumference
💡Diameter
💡Cartwheel
💡Cardboard
💡Subscribe
💡Algorithm
💡Radius
💡Death Ray
💡Practice
Highlights
The number pi is approximately equal to 3.14, a fact that was first worked out by Archimedes.
Archimedes discovered that the circumference of a circle is 3.14 times its diameter.
The method used by Archimedes did not involve sophisticated tools, only a cartwheel.
A cardboard from a cereal box is used to demonstrate the concept of pi in a modern reenactment.
The cardboard is carefully cut and prepared to represent the 'road' for the wheel to roll on.
A wheel is constructed using a compass or a round object to draw a circle.
The wheel's axle and wooden planks are detailed to mimic an ancient design.
The wheel is rolled along the 'road' to mark the circumference on the cardboard.
The relationship between the circumference and the diameter is explored by marking multiples of the diameter.
The value of pi is derived from the number of diameters it takes for the wheel to complete one cycle.
The practical demonstration shows that pi equals approximately 3.14, aligning with Archimedes' findings.
The video explains the formula for the circumference of a circle as 2 * pi * r.
A practical calculation is performed to verify the relationship between pi, radius, and circumference.
The video concludes that Archimedes' method of determining pi is both simple and effective.
The presenter encourages viewers to subscribe for more drawing and educational content.
A call to support the channel is made, with links provided in the description for Patreon and other platforms.
The presenter shares a personal connection to the topic, having written a book about Archimedes.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: