The Chain Rule

StatQuest with Josh Starmer

12 Jul 202018:23

EducationalLearning

32 Likes 10 Comments

TLDRIn this StatQuest episode, Josh Starmer explores the chain rule in calculus with a clear and engaging explanation. Starting with a quick review of derivatives, he dives into the chain rule using simple examples like predicting shoe size from weight and height. He then tackles more complex scenarios, such as modeling hunger and ice cream cravings, demonstrating how the chain rule is applied in real-world data analysis. The video concludes with an application of the chain rule to the residual sum of squares in machine learning, showing how it helps find the best fit line for data.

Takeaways

📚 The Chain Rule is a fundamental concept in calculus that helps in finding the derivative of a composite function.
🔍 The video assumes viewers have a basic understanding of derivatives and aims to provide a deeper insight into the Chain Rule.
📈 The Chain Rule is introduced using a simple example involving predicting shoe size from weight through the intermediate variable of height.
📝 The Power Rule is reviewed as a foundation for understanding the Chain Rule, which involves multiplying the variable by its power and then adjusting for the power change.
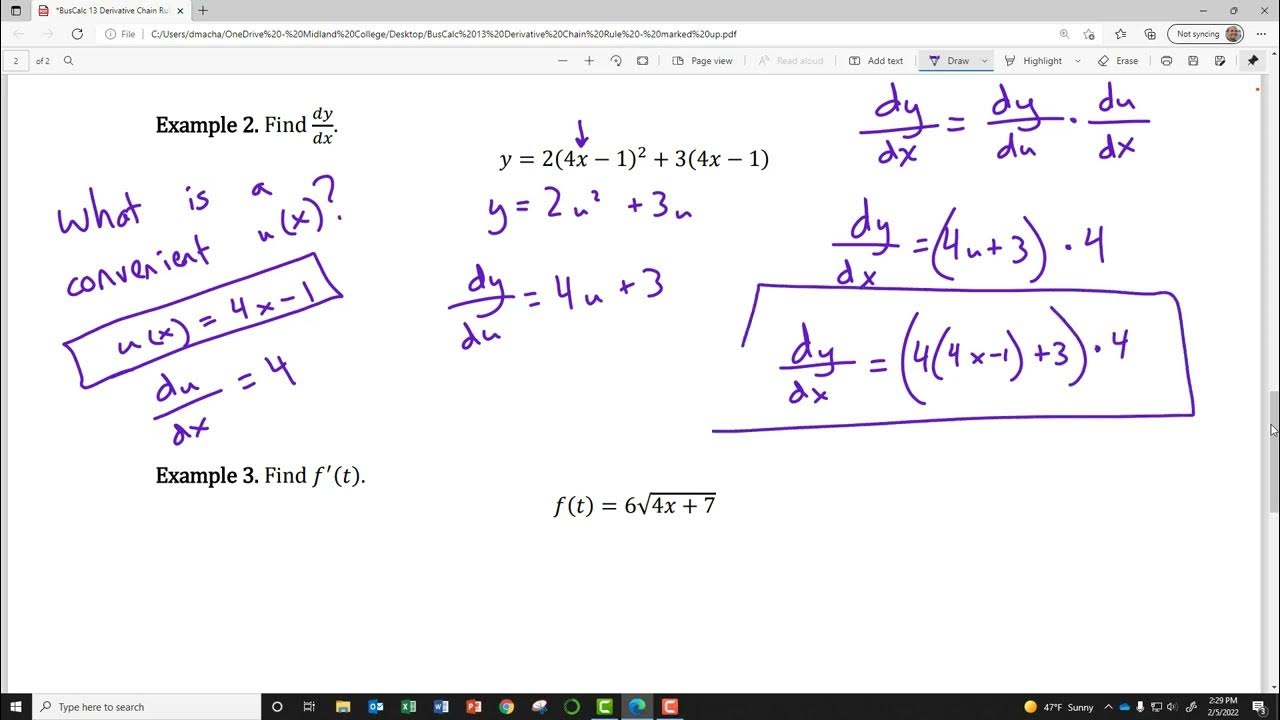
🤔 The Chain Rule is applied to a scenario where the relationship between variables is not immediately obvious and requires breaking down the composite function.
📊 The script uses visual examples with graphs to illustrate how derivatives are calculated and the Chain Rule is applied.
🔢 The Chain Rule formula is demonstrated as the product of the derivative of the outer function with respect to the inner function and the derivative of the inner function with respect to the variable.
🍦 An example involving hunger and craving for ice cream is used to show the application of the Chain Rule in a more complex scenario with exponential and square root functions.
📉 The Chain Rule is also applied to the context of machine learning, specifically in minimizing the residual sum of squares for a linear regression model.
🔧 The process of finding the best fit line by minimizing the squared residual involves using the Chain Rule to find where the derivative of the squared residual equals zero.
🎯 The final takeaway is the practical application of the Chain Rule in fitting a line to data, which helps in determining the optimal intercept for the best fit.

Q & A

What is the main topic of the video?
-The main topic of the video is the chain rule in calculus, with a focus on its application and deeper understanding.
What is the chain rule?
-The chain rule is a fundamental theorem in calculus that allows for the calculation of the derivative of a composite function, stating that the derivative of the composite function is the product of the derivative of the outer function and the derivative of the inner function.
Why is the chain rule important in the context of the video?
-The chain rule is important because it helps in understanding how changes in one variable can affect another through a series of interconnected functions, which is demonstrated through various examples in the video.
What is the purpose of the parabola example in the video?
-The parabola example serves as a quick review of derivatives, showing how the slope of the tangent line at any point on the curve can be found using the derivative of the equation representing the parabola.
How is the chain rule demonstrated in the context of weight, height, and shoe size?
-The chain rule is demonstrated by showing how an increase in weight can predict an increase in height, and then using the predicted height to predict shoe size, with the overall change in shoe size being the product of the two individual derivatives.

Outlines

00:00

📚 Introduction to the Chain Rule

Josh Starmer of StatQuest introduces the concept of the chain rule in calculus, assuming the audience has a basic understanding of derivatives. He provides a quick review of derivatives using a parabola as an example, explaining how the derivative can be used to find the slope of the tangent line at any point on the curve. The power rule is also briefly reviewed before delving into the chain rule with a simple example involving predicting height and shoe size from weight measurements.

05:02

🔗 Applying the Chain Rule to Predictive Models

The script explains the application of the chain rule in the context of predictive models, using the relationships between weight, height, and shoe size as an example. It demonstrates how to calculate the derivative of shoe size with respect to weight by multiplying the derivatives of the intermediate steps (height with respect to weight and shoe size with respect to height). The chain rule is then illustrated with a more complex example involving hunger and ice cream cravings, showing how to find the derivative of cravings with respect to time since the last snack by using the chain rule.

10:03

📉 Chain Rule in Residual Sum of Squares

The video script discusses the application of the chain rule in the context of the residual sum of squares, a loss function used in machine learning. It uses a simple linear model to fit weight and height measurements, focusing on adjusting the intercept to minimize the squared residuals. The chain rule is used to find the derivative of the squared residual with respect to the intercept, which is then set to zero to find the optimal intercept value that minimizes the loss function. The process involves substituting the predicted height equation into the residual equation and simplifying using the chain rule.

15:05

🎯 Conclusion and Call to Action

In the final paragraph, Josh Starmer concludes the video by summarizing the application of the chain rule in various contexts, including predictive modeling and loss function minimization. He encourages viewers to subscribe for more content, support StatQuest through Patreon, become a channel member, purchase study guides, apparel, or make a donation. Links to these options are provided in the video description.

Mindmap

Keywords

💡Chain Rule

The Chain Rule is a fundamental concept in calculus that allows for the computation of the derivative of a composite function. In the video, it is explained as the method to determine how a change in one variable (e.g., weight) can lead to a change in another variable (e.g., shoe size) through an intermediate variable (e.g., height). The Chain Rule is central to the video's theme of understanding complex relationships between variables.

💡Derivative

A derivative in calculus represents the rate at which a function changes with respect to its variable. In the context of the video, derivatives are used to find the slope of a tangent line at any point on a curve, indicating how quickly a variable like 'awesomeness' changes with respect to 'likes for StatQuest'.

💡Power Rule

The Power Rule is a basic principle in calculus for finding the derivative of a function that involves a variable raised to a power. The video demonstrates the Power Rule by showing how to calculate the derivative of 'awesomeness' with respect to 'likes for StatQuest squared', which simplifies to twice the 'likes for StatQuest'.

💡Tangent Line

A tangent line is a straight line that touches a curve at a single point without crossing it. In the video, the slope of the tangent line is used to represent the instantaneous rate of change of a variable, such as the change in 'awesomeness' with respect to 'likes for StatQuest'.

💡Slope

Slope is a measure of the steepness of a line, indicating the rate of change between two variables. The video uses the concept of slope to explain how changes in one variable (like weight) can predict changes in another (like height or shoe size) through the use of the Chain Rule.

💡Residual

In statistics, a residual is the difference between the observed value and the value predicted by a model. The video discusses how to calculate residuals to evaluate the fit of a line to data and how to minimize these residuals to improve the model's accuracy.

💡Residual Sum of Squares

Residual Sum of Squares (RSS) is a measure used in regression analysis to assess the fit of a model to data. The video explains how to use the derivative of the RSS with respect to the intercept to find the best-fitting line for a given set of data points.

💡Intercept

The intercept of a line in a linear equation represents the point where the line crosses the y-axis. In the video, adjusting the intercept of a line is shown as a way to minimize the squared residual, thereby improving the fit of the line to the data.

💡Exponential Function

An exponential function is a mathematical function where the variable is in the exponent. The video uses an exponential function to model how hunger increases over time since the last snack, demonstrating how the rate of increase accelerates.

💡Square Root Function

A square root function is a mathematical function that involves the square root of its input. The video uses a square root function to model the craving for ice cream based on hunger levels, showing how the craving does not increase linearly but rather tapers off as hunger increases.

💡Machine Learning

Machine learning is a subset of artificial intelligence that enables systems to learn and improve from experience without being explicitly programmed. The video briefly touches on the application of the Chain Rule in the context of machine learning, specifically in the calculation of the derivative of a loss function like the residual sum of squares.

Highlights

Introduction to the Chain Rule in the context of derivatives and its deeper understanding.

Quick review of the basic concept of a derivative using a parabola as an example.

Explanation of the power rule for calculating derivatives.

Introduction of the Chain Rule with a simple example involving weight, height, and shoe size.

Derivation of the relationship between weight and height using the slope of a fitted line.

Derivation of the relationship between height and shoe size with a unique example.

Application of the Chain Rule to predict shoe size from weight by combining two derivatives.

Use of the Chain Rule in a more complex example involving hunger and craving for ice cream.

Derivation of the relationship between time since the last snack and hunger using an exponential model.

Derivation of the craving for ice cream with respect to hunger using a square root function.

Application of the Chain Rule to find the rate of change of craving ice cream with respect to time since the last snack.

Explanation of how to apply the Chain Rule when equations are not separate but combined.

Technique of using parentheses to simplify the application of the Chain Rule in complex equations.

Application of the Chain Rule to the residual sum of squares in machine learning.

Derivation of the best fitting line using the Chain Rule and the concept of residuals.

Finding the intercept that minimizes the squared residual using the Chain Rule.

Transcripts

Browse More Related Video

Machine Learning from First Principles, with PyTorch AutoDiff — Topic 66 of ML Foundations

Math 1325 Lecture 9 6 Chain & Power Rule

The Chain Rule - More Examples

BusCalc 13 Derivative Chain Rule

Calculus AB Lesson 3.4 The Chain Rule

Math 11- Section 2.6 (previously section 3.5)