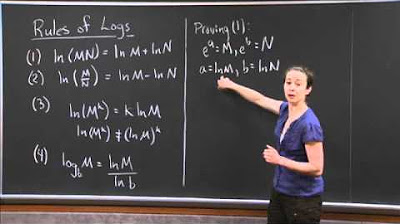Math 11- Section 2.6 (previously section 3.5)
TLDRIn this educational transcript, Professor Monte dives into the world of calculus, focusing on the derivatives of exponential functions 'a to the power of x' and logarithmic functions 'log base a of x'. He introduces two key rules for derivatives, providing a proof for the first one and emphasizing the importance of the chain rule. The professor then demonstrates the application of these rules through a series of examples, including differentiating various exponential and logarithmic expressions. He also touches on the product rule and its application in more complex scenarios. The transcript concludes with real-world applications, such as modeling the recycling rate of aluminum cans and predicting the financial liability of US households, using exponential growth and decay. The professor's approach is methodical, ensuring that the concepts are well explained and the examples are worked through step by step, offering learners a comprehensive understanding of the subject matter.
Takeaways
- 📖 The derivative of a function in the form of a^x, where a is the base, is a^x × ln(a).
- 👇 For any base a (except 1 and negative numbers), the derivative of a^x remains a^x × ln(a), highlighting the importance of the natural logarithm of the base.
- 📊 The derivative of the natural logarithm function ln(x) is 1/x, which is a fundamental rule in calculus.
- 🔗 The chain rule is essential when differentiating composite functions, such as e^(ax), where the derivative is a × e^(ax).
- 📐 The derivative of a logarithmic function with a different base, log_a(x), is 1/(x × ln(a)), which is derived from the basic logarithmic derivative rule.
- 📣 The natural logarithm of e, denoted as ln(e), is equal to 1, simplifying the derivative of e^x to just e^x.
- ✅ Practice is key to mastering derivatives, as demonstrated by the numerous examples provided in the script, including both basic and complex functions.
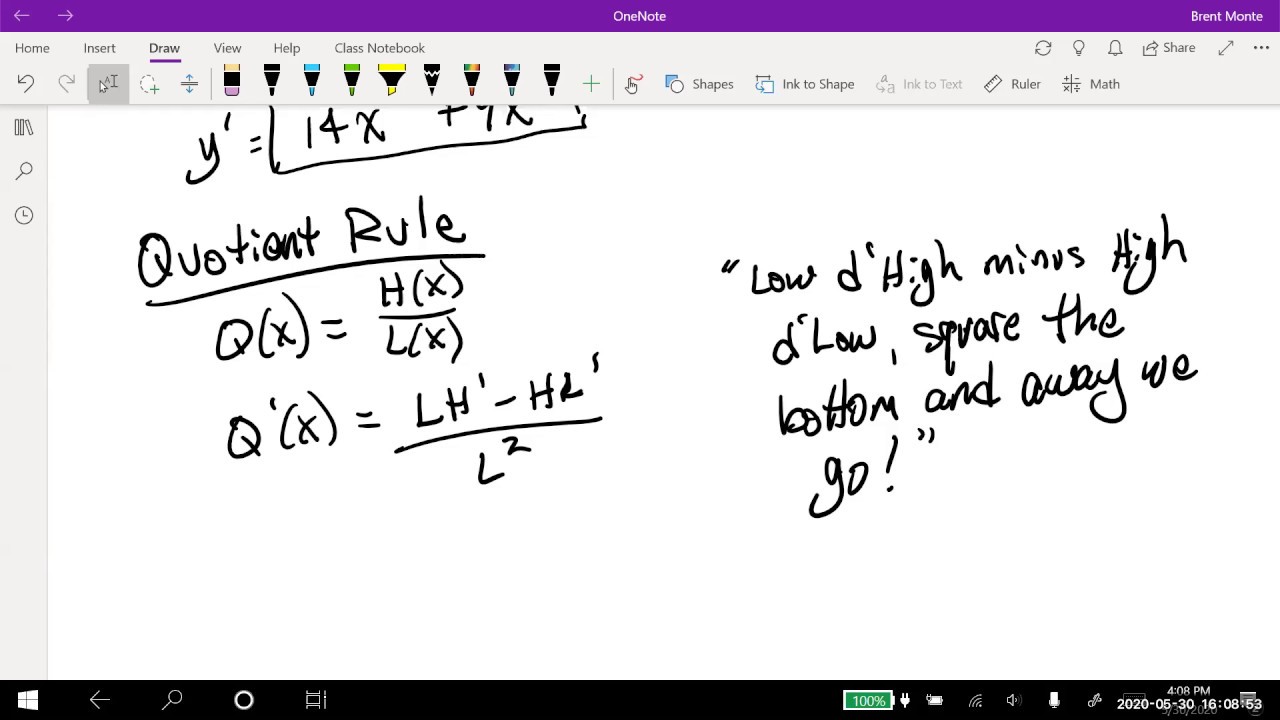
- 🔑 The product rule is frequently used in calculus to find the derivative of a product of two functions, and it was demonstrated with various examples.
- 📉 The concept of recycling and financial liability was used to apply the derivative in real-world scenarios, illustrating the practical use of calculus.
- 📌 The rate of change, as indicated by the derivative, can be used to predict future values or trends in applications, such as the amount of aluminum in circulation or financial liability.
- 🔢 Interpreting the derivative in context is crucial for understanding its implications, such as the expected increase or decrease in quantities over time.
Q & A
What is the derivative of a to the power of x with respect to x?
-The derivative of a^x with respect to x is a^x times the natural logarithm of a (Ln(a)).
What is the rule for the derivative of the natural logarithm of x?
-The derivative of the natural logarithm of x (Ln(x)) is 1/x.
How does the derivative of e to the power of x compare to the derivative of a to the power of x?
-The derivative of e^x is simply e^x, whereas the derivative of a^x involves multiplying the entire exponential (a^x) by the natural logarithm of the base 'a' (Ln(a)).
What is the role of the chain rule in differentiating exponential functions with a variable base?
-The chain rule is used to differentiate the exponent of the exponential function. If the base 'a' is a constant and 'x' is the variable, the derivative involves multiplying the exponential function by the natural logarithm of 'a' (Ln(a)).
What is the derivative of the logarithm of x to a different base 'a'?
-The derivative of the logarithm of x to base 'a' (log_a(x)) is 1/(x * Ln(a)).
Why is it important to remember the chain rule when differentiating exponential and logarithmic functions?
-The chain rule is essential for differentiating functions that involve composite functions, such as exponential functions with a variable base or logarithms to a base other than 'e'. It allows you to correctly apply the derivative to the inner function and then multiply by the derivative of the outer function.
How does the base of the logarithm affect the derivative of the logarithmic function?
-The base of the logarithm affects the derivative by being included in the derivative formula as a multiplicative factor. Specifically, the derivative includes '1/Ln(base)', which becomes '1/Ln(e)' or simply '1' when the base is 'e'.
What is the significance of the product rule in differentiating functions that are a product of two functions?
-The product rule is used to find the derivative of a function that is the product of two other functions. It states that the derivative of such a function is the first function times the derivative of the second plus the second function times the derivative of the first.
How does the concept of 'rate of change' relate to the derivative of a function?
-The derivative of a function at a certain point represents the rate of change or the slope of the function at that point. It is a measure of how the function's value changes with respect to changes in the input variable.
In the context of the script, what does 'n prime of T' represent?
-In the context of the script, 'n prime of T' represents the derivative of the function 'n of T', which is the rate of change of the number of pounds of aluminum in use with respect to time 'T'.
How does the script demonstrate the application of derivatives in real-world problems?
-The script demonstrates the application of derivatives in real-world problems by showing how to calculate the rate of change over time for two different scenarios: the recycling of aluminum cans and the growth of financial liability of US households. It uses derivatives to predict future values and interpret the results.
Outlines
📚 Introduction to Derivatives of Exponential and Logarithmic Functions
Professor Monte introduces the topic of derivatives, focusing on the derivatives of a^x and log_a(x). He outlines two main methods for finding these derivatives and emphasizes the importance of the chain rule. The professor also provides a proof for the derivative of a^x, highlighting the role of logarithms in simplifying the process.
🔑 Derivative Rules for Exponential and Logarithmic Functions
The video covers the rules for derivatives of exponential functions with any base 'a' and logarithmic functions with any base 'a'. It is shown that the derivative of a^x involves multiplying the base 'a' raised to the power of 'x' by the natural logarithm of 'a'. Similarly, the derivative of log_a(x) is derived, which involves the reciprocal of 'x' and the natural logarithm of the base 'a'.
📝 Application of Derivative Rules through Examples
The professor works through several examples to demonstrate the application of the derivative rules for exponential and logarithmic functions. He uses the product rule and chain rule where necessary, showing how to factor out common terms and simplify expressions. The examples include varying bases for the exponential function and differentiating more complex expressions involving powers and products.
🧮 Factoring and Simplifying Derivatives
The process of factoring out common terms in derivatives is emphasized, with a focus on cleanly presenting the derivative of a combined power and exponential function. The professor also discusses the importance of not misinterpreting the chain rule and correctly applying it to find derivatives of more complex functions.
📈 Derivatives in Real-World Applications
The professor explores real-world applications of derivatives, such as modeling the recycling rate of aluminum cans and the financial liability of US households. He demonstrates how to use the given formulas to find the rate of change over time, interpret the meaning of the derivative in context, and predict future values based on the model.
📊 Interpreting Derivatives for Predictive Analysis
The video concludes with an interpretation of the derivative in the context of the financial liability model. The professor calculates the derivative for a specific year and interprets it to predict the expected increase in household liability for the subsequent year, emphasizing the forward-looking nature of derivatives in predictive analysis.
🎓 Summary of Key Takeaways
The professor summarizes the key takeaways from the lesson, which include the derivative rules for a^x and log_a(x). He encourages practice with the provided examples and assures students that with time and effort, they can master the concepts of derivatives and their applications.
Mindmap
Keywords
💡Derivative
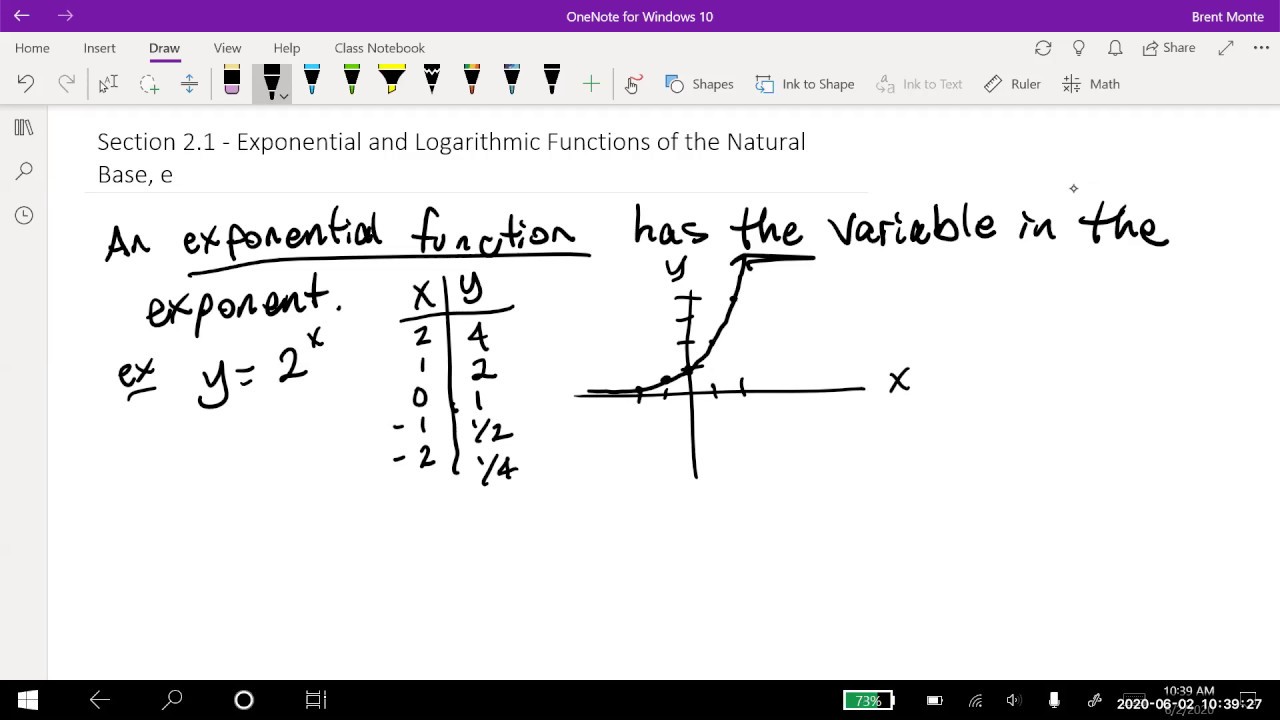
💡Exponential Function
💡Logarithm
💡Chain Rule
💡Product Rule
💡Logarithmic Properties
💡Exponential Growth/Decay
💡Ln (Natural Logarithm)
💡Proof
💡Applications of Derivatives
💡Function Modeling
Highlights
Derivatives of a^x and log base a of x are discussed with two methods shown.
The derivative of ln(x) is 1/x, and the derivative of e^x is e^x itself.
Derivative of a^x is a^x times the natural log of the base 'a'.
For a different base than e, the derivative involves multiplying by the natural log of that base.
A proof is provided for the derivative of a^x using properties of logarithms and the chain rule.
The derivative of log base a of x is 1/(x * ln(a)) for any base 'a'.
Product rule is applied when differentiating composite functions, such as x^3 * 5.4^x.
The chain rule is emphasized for its importance in differentiating exponential and logarithmic functions.
Examples are provided to illustrate the process of differentiating various functions involving exponentials and logarithms.
The concept of relative extrema is mentioned in the context of factoring out common terms in derivatives.
Interpretation of derivatives in real-world applications, such as recycling rates and financial liabilities, is discussed.
A step-by-step approach to solving derivative problems is emphasized for clarity and understanding.
The importance of understanding the rate of change represented by the derivative is highlighted in the context of applications.
The derivative of a function modeling the total financial liability of US households is calculated.
Interpretation of the derivative in terms of expected increase in household liability is provided.
The two key takeaways are the derivatives of a^x and log base a of x, which are foundational for the rest of the material.
The importance of practice and re-evaluation of problems to solidify understanding is encouraged.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: