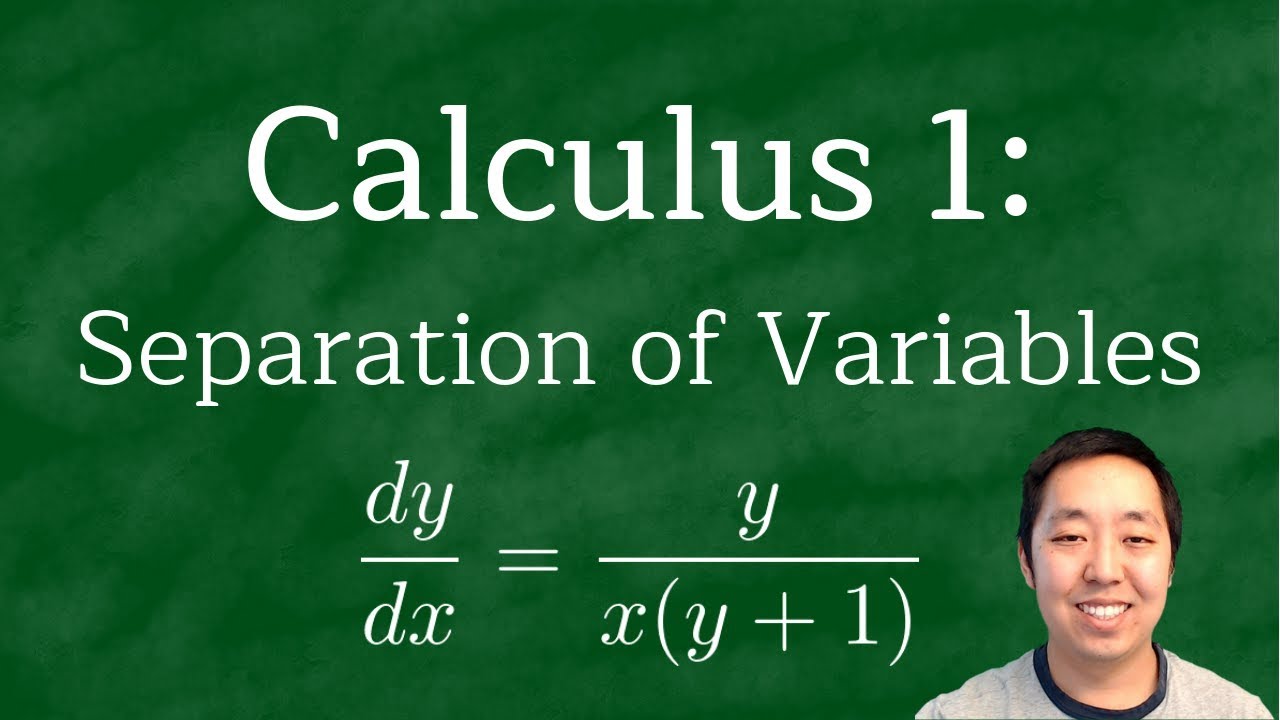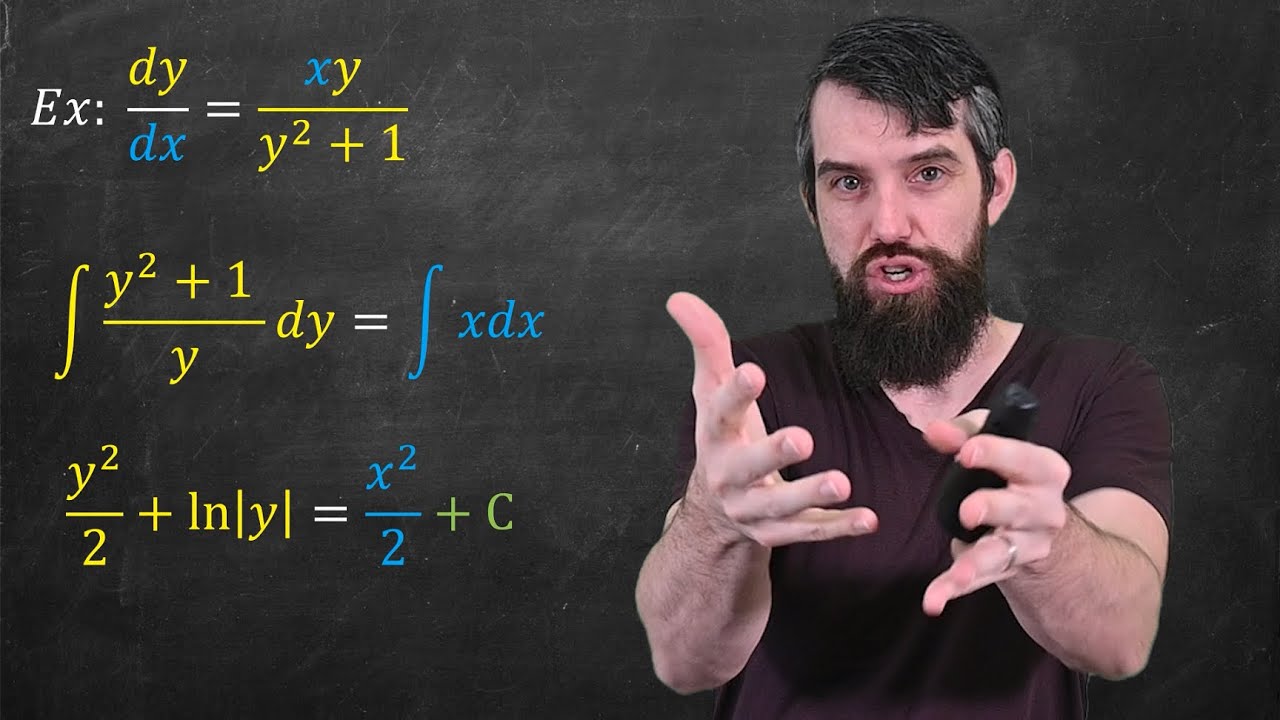SC_V1_1 ODE Trick: Separation of Variables (Leibniz Rule)

C-RAM

28 Dec 201904:05

EducationalLearning

32 Likes 10 Comments

TLDRThis video script delves into the method of separation of variables for solving ordinary differential equations (ODEs). It highlights the rarity of ODEs with solvable probability density functions and introduces a historical approach attributed to Leibniz. The script guides viewers through the process of separating variables, integrating both sides, and finding an explicit solution for a given ODE example, showcasing a step-by-step method to arrive at the solution involving exponential functions and constants.

Takeaways

📚 The video introduces the concept of separation of variables for solving ordinary differential equations (ODEs).
📈 Only a few ODEs have probability density functions that can be expressed in closed form, but the solution methods are rooted in traditional calculus tricks.
🎓 The audience is encouraged to feel part of a lineage and tradition of mathematical problem-solving, dating back to the time of Leibniz.
🔍 The ODE of interest has a vector field that is the product of a deterministic function of time and a function that depends only on the state variable.
👨‍🏫 The method to solve such ODEs was pioneered by Professor Leibniz, known for his mathematical genius and the famous 'Leibniz's biscuits'.
📝 The solution involves rewriting the ODE to separate the variables, integrating both sides with respect to their respective variables, and finding an explicit solution for the product of the variables.
📑 The example provided in the script demonstrates the process of solving an ODE where the derivative with respect to time is proportional to the product of time and the state variable.
✏️ The first step in solving the example ODE is to rewrite it to separate the time (T) and state variable (X) components.
🧮 After rewriting, the next step is to integrate both sides of the equation separately with respect to X and T, resulting in logarithmic and polynomial expressions.
🔍 The third step involves solving for the explicit solution of the product XT, which involves manipulating the integrated expressions to isolate the variables.
📘 The final solution for the example given is expressed as XT = e^(T^2) * a, where 'a' is a new constant defined to represent the exponential of the difference between two integrating constants.

Q & A

What is the main concept introduced in the video?
-The main concept introduced in the video is the method of separation of variables for solving ordinary differential equations (ODEs).
Why is it rare to express the probability density function of a stochastic differential equation in closed form?
-It is rare because only a very few stochastic differential equations have solutions that can be expressed in a closed form, making the solution process more complex and less straightforward.
Add the missing question and answer here
-Add the corresponding answer here

Outlines

00:00

📚 Introduction to Separation of Variables in ODEs

This paragraph introduces the audience to the method of separation of variables for solving ordinary differential equations (ODEs). It emphasizes that few ODEs have probability density functions that can be expressed in closed form, but the techniques to solve them are rooted in traditional calculus. The script mentions the equation of interest, which involves a function of time and a state variable, and outlines the steps to solve it using a method attributed to Leibniz. The example provided involves rewriting the ODE to separate the variables and then integrating both sides with respect to their respective variables.

Mindmap

Keywords

💡Separation of Variables

Separation of variables is a method used in solving differential equations by rearranging the equation so that all terms involving one variable are on one side and all terms involving the other variable are on the other side. In the context of the video, it is applied to ordinary differential equations (ODEs) to simplify the process of finding a solution. The script mentions that this technique is rooted in calculus and has been taught for centuries, emphasizing its importance in solving the given ODE where the vector field is a product of functions of time and the state variable.

💡Ordinary Differential Equation (ODE)

An ordinary differential equation is a differential equation containing one or more derivatives of a function of a single variable. In the video, the ODE of interest is one where the current slope is related to the product of a deterministic function of time and another function that depends only on the state variable. The script uses an ODE as an example to demonstrate the separation of variables technique, highlighting its relevance in finding solutions to such equations.

💡Probability Density Function

A probability density function is a function that describes the likelihood of a continuous random variable taking on a particular value. The script notes that very few ODEs have probability density functions that can be expressed in closed form, indicating the complexity and the special nature of the equations that can be solved using the separation of variables method.

💡Vector Field

In the context of differential equations, a vector field represents the direction and magnitude of the rate of change of a variable. The script refers to the right-hand side of the ODE as a vector field, which in the given example coincides with the product of a function of time and a function of the state variable, allowing for the application of the separation of variables technique.

💡Deterministic Function

A deterministic function is one where for every input, there is a specific and predictable output. In the script, the deterministic function of time, denoted as G of T, is multiplied by another function to form the vector field in the ODE, which is a key component in the separation of variables method.

💡Leibniz

Gottfried Wilhelm Leibniz was a prominent philosopher and mathematician known for his contributions to calculus and other fields. The script humorously refers to 'Leibniz's secret cooking recipe' as a metaphor for the method of separation of variables attributed to him, emphasizing the historical importance of his work in this area.

Highlights

Introduction to the concept of separation of variables for solving ordinary differential equations (ODEs).

Few ODEs have a probability density function that can be expressed in closed form.

The solution process is rooted in calculus tricks from ODE calculus.

Participation in a lineage and tradition of mathematical problem-solving.

The differential equation of interest has a vector field that coincides with the product of two functions.

Leibniz's method for solving ODEs is referenced.

Leibniz is known for his mathematical contributions and his 'beautiful bisquit'.

A step-by-step recipe from Leibniz's 'cookbook' for solving the ODE.

Integration of both sides of the equation with respect to their variables.

Finding an explicit solution for the product of X and T.

Example ODE provided with the equation dX/DT = 2T * X.

The vector field is a product of time and the state variable, making Leibniz's method applicable.

Rewriting the ODE to separate time from state as the first step.

Integration of both sides of the equation leads to logarithmic and quadratic forms.

Solving for the logarithmic form to find an explicit solution for X * T.

Exponential transformation of the equation to isolate constants.

Separation of exponential terms and introduction of a new constant 'a'.

Transcripts

Browse More Related Video

SC_V1_2 Integrating Factor to Solve Linear ODEs

Lec 1 | MIT 18.03 Differential Equations, Spring 2006

Calculus 1: Separation of Variables Examples

Initial Value Problem

Separation of Variables // Differential Equations

Linear Differential Equations & the Method of Integrating Factors