Equations of motion examples (Higher Physics)

Mr Smith's Physics online
21 Aug 201613:46
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script covers the equations of motion, guiding viewers through the derivation process and highlighting key points. It presents three typical problems involving motion equations, encouraging viewers to solve them before revealing the answers. The script explains how to calculate acceleration and time for a car entering a motorway, a trolley's acceleration from rest, and the time and height of a ball thrown vertically upwards. The video emphasizes the importance of using the correct equations and significant figures, aiming to enhance understanding of motion dynamics.

Takeaways
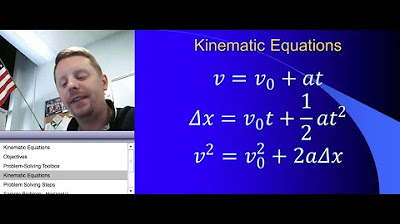
  • 📚 The video explains how to derive the equations of motion and provides important points to remember when using them.
  • 🚗 The first question involves a car accelerating uniformly from 13 m/s to 31 m/s over a distance of 220 meters, requiring the calculation of the car's acceleration.
  • ✏️ For the first question, the displacement is 220 meters, initial velocity is 13 m/s, final velocity is 31 m/s, and the acceleration is unknown.
  • 🧮 Using the equation V² = U² + 2as, the acceleration is calculated to be 1.8 m/s².
  • ⏱️ Part B of the first question involves calculating the time taken for the car to accelerate, using the equation V = U + at, resulting in a time of 10 seconds.
  • 🛒 The second question involves a trolley running down a track from rest to a speed of 2.77 m/s over a distance of 1.20 meters, requiring the calculation of the trolley's acceleration.
  • 🔢 Using the same equation V² = U² + 2as, the acceleration is calculated to be 3.20 m/s² for the trolley.
  • ⏲️ Part B of the second question involves calculating the time taken for the trolley to travel 1.20 meters, using V = U + at, resulting in a time of 0.866 seconds.
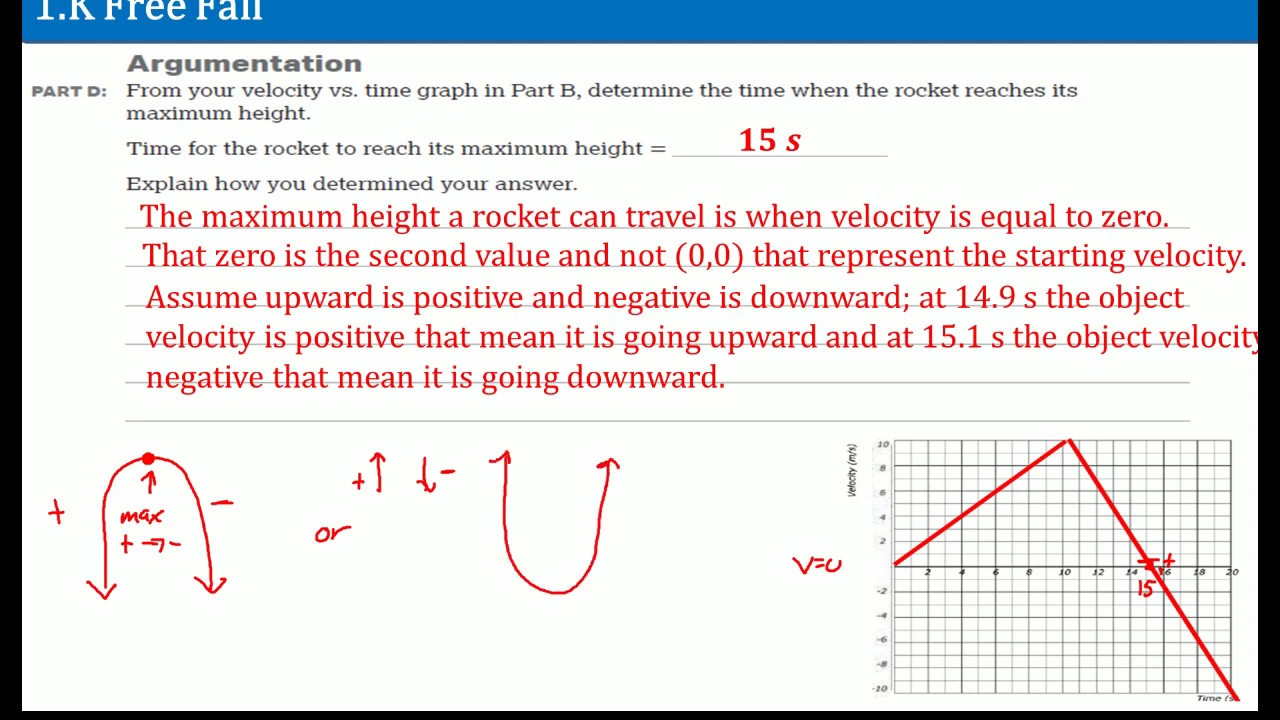
  • 🏀 The third question involves a ball thrown vertically upwards with an initial velocity of 24.5 m/s, requiring the calculation of the time taken to reach maximum height.
  • 📏 Using the equation V = U + at, the time to reach maximum height is calculated to be 2.5 seconds.
  • 🧗‍♂️ Part B of the third question involves calculating the gain in height of the ball during this time, using the equation s = ut + 0.5at², resulting in a height of 30.6 meters.
Q & A

  • What is the initial velocity of the car in the first question?

    -The initial velocity of the car is 13 meters per second.

  • What equation is used to calculate acceleration in the first question?

    -The equation used to calculate acceleration is V² = U² + 2aS.

  • How do you rearrange the equation V² = U² + 2aS to solve for acceleration (a)?

    -You rearrange the equation to solve for acceleration by isolating 'a' on one side: a = (V² - U²) / (2S).

  • What is the final calculated acceleration of the car in the first question?

    -The final calculated acceleration of the car is 1.8 meters per second squared.

  • How is the time taken for the car to accelerate calculated in Part B of the first question?

    -The time is calculated using the equation V = U + at and solving for t.

  • What is the acceleration of the trolley in the second question?

    -The acceleration of the trolley is 3.20 meters per second squared.

  • Which equation is used to find the acceleration of the trolley in the second question?

    -The equation used is V² = U² + 2aS.

  • How do you calculate the time taken for the trolley to travel 1.20 meters in the second question?

    -The time is calculated using the equation V = U + at and solving for t.

  • What is the initial velocity of the ball in the third question?

    -The initial velocity of the ball is 24.5 meters per second.

  • How is the maximum height achieved by the ball calculated in Part B of the third question?

    -The maximum height is calculated using the equation S = Ut + 0.5at² and substituting the known values.

Outlines
00:00
🚗 Car Acceleration Calculation

The first paragraph introduces a video script that discusses the equations of motion, specifically addressing three typical questions. The first question involves calculating the acceleration of a car that uniformly accelerates from 13 m/s to 31 m/s over a distance of 220 meters. The key equation used is V² = U² + 2as, where V is the final velocity, U is the initial velocity, a is the acceleration, and s is the displacement. The solution involves algebraic manipulation to solve for a, resulting in an acceleration of 1.8 m/s². The second part of the question asks for the time taken for this acceleration, using the rearranged equation V = U + at, leading to a time of 10 seconds.

05:02
🏎 Trolley Acceleration from Rest

The second paragraph continues the theme of motion equations by presenting a scenario where a trolley accelerates from rest, reaching a speed of 2.77 m/s over a distance of 1.20 meters. The goal is to find the acceleration. Using the equation V² = U² + 2as, and knowing that the initial velocity U is zero, the calculation leads to an acceleration of 3.20 m/s². The subsequent part of the question asks for the time taken to travel the distance, which is found using the equation V = U + at, yielding a time of approximately 0.86 seconds.

10:04
🏐 Ball's Vertical Motion Analysis

The third paragraph shifts the focus to vertical motion, describing a ball thrown upwards with an initial velocity of 24.5 m/s. The task is to calculate the time to reach the maximum height and the height itself. The analysis uses the equation V = U + at, with a negative acceleration due to gravity (-9.8 m/s²), resulting in a time of 2.5 seconds to reach the peak. For the height calculation, the kinematic equation s = ut + 0.5at² is employed, combining the initial velocity, time, and acceleration to find the maximum height of approximately 30.6 meters.

Mindmap
Keywords
💡Equations of Motion
The equations of motion are fundamental principles in physics that describe the relationship between an object's velocity, acceleration, displacement, and time. In the video, these equations are used to solve problems involving the acceleration of a car, the time taken for a trolley to travel a certain distance, and the trajectory of a ball thrown vertically upwards. The script demonstrates how to derive and apply these equations to practical scenarios.
💡Acceleration
Acceleration is the rate of change of velocity of an object with respect to time. It is a vector quantity that has both magnitude and direction. In the context of the video, acceleration is calculated for a car entering a motorway and for a trolley running down a track, illustrating how the concept is central to understanding changes in velocity.
💡Uniform Acceleration
Uniform acceleration refers to a constant rate of change of velocity. The video script describes a car that accelerates uniformly from one speed to another, covering a specific distance, which is a classic example of using the equations of motion with uniform acceleration.
💡Displacement
Displacement is the change in position of an object. It is a vector quantity that refers to the distance between the initial and final positions. In the video, displacement is given as a known quantity when calculating the acceleration of the car and the distance traveled by the trolley.
💡Initial Velocity
Initial velocity is the velocity of an object at the start of its motion. The script mentions the initial velocity of the car and the trolley, which is a necessary value for calculating acceleration using the equations of motion.
💡Final Velocity
Final velocity is the velocity of an object at the end of the time period under consideration. The video uses the final velocity of the car and the trolley to demonstrate how to find unknown quantities such as acceleration and time.
💡Time
Time is the independent variable in the equations of motion, representing the duration of motion. The script discusses how to calculate the time taken for the car to accelerate and for the trolley to travel a certain distance when the acceleration is known.
💡Vertical Motion
Vertical motion refers to the movement of an object in the upward or downward direction. The video addresses a problem involving a ball thrown vertically upwards, where the equations of motion are applied to calculate the time to reach the maximum height and the height itself.
💡Significant Figures
Significant figures are the digits in a number that carry meaning contributing to its precision. The script emphasizes the importance of reporting results to an appropriate number of significant figures, as seen when rounding the acceleration of the trolley and the time taken for the ball to reach its maximum height.
💡Calculator
A calculator is a device used to perform arithmetic operations. In the script, the presenter uses a calculator to perform the mathematical computations required to solve the motion problems, demonstrating the practical application of tools in physics problem-solving.
💡Physics Podcast
The Physics Podcast is mentioned as a resource for more information on the equations of motion and related topics. It serves as an educational platform where viewers can find additional materials and upcoming videos to enhance their understanding of physics concepts.
Highlights

Introduction to the video on equations of motion and their derivation.

Invitation to pause and attempt questions before viewing the solution.

Problem setup for calculating the acceleration of a car from 13 m/s to 31 m/s over 220 meters.

Use of the equation V^2 = U^2 + 2as to find acceleration.

Explanation of why all values can be considered positive in this scenario.

Calculation of acceleration using the rearranged equation (31^2 = 13^2 + 2 * a * 220).

Result of the car's acceleration calculation: 1.8 m/s^2.

Transition to calculating the time taken for the car to accelerate.

Use of the equation V = U + at to find the time.

Result of the time calculation: 10 seconds.

Introduction to the second problem involving a trolley's acceleration.

Calculation of the trolley's acceleration using the equation V^2 = U^2 + 2as.

Result of the trolley's acceleration: 3.20 m/s^2.

Calculation of the time taken for the trolley to travel 1.20 meters.

Result of the trolley's travel time: approximately 0.86 seconds.

Introduction to the third problem involving a ball thrown vertically upwards.

Use of the equation V = U + at to find the time to reach maximum height.

Result of the time calculation for the ball to reach maximum height: 2.5 seconds.

Calculation of the maximum height reached by the ball using the equation s = ut + 0.5at^2.

Result of the maximum height calculation: 30.6 meters.

Encouragement to visit physics-podcast.co.uk for more information and upcoming videos.

Transcripts

Browse More Related Video

Kinematics Part 2: Vertical Motion

AP Physics B Kinematics Presentation #38

Choosing kinematic equations | One-dimensional motion | AP Physics 1 | Khan Academy

AP Physics Workbook 1.K Free Fall

High School Physics: Kinematic Equations

Uniform Circular Motion Problems

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Motion EquationsPhysics TutorialAccelerationVelocityDisplacementEducational ContentVideo SeriesProblem SolvingScience LearningKinematicsDynamics