Derivative Tricks (That Teachers Probably Don't Tell You)
TLDRIn this educational video, Brian introduces three derivative tricks to simplify calculus problems. The first trick involves taking the derivative of a square root by simply multiplying it by 1/2. The second trick is a shortcut for derivatives of reciprocal functions, where flipping the sign, multiplying by the exponent, and adding one to the exponent in the denominator streamlines the process. The final trick is a unique application of logarithmic differentiation for complex quotients, which avoids cumbersome quotient and chain rules. These tips aim to make derivative calculations faster and more efficient.
Takeaways
- 📚 The first trick is a shortcut for differentiating the square root of a function, which simplifies to \( \frac{1}{2} \times \sqrt{x} \).
- 🔑 A mnemonic for this trick is to remember that the derivative of a square root is half of the square root itself.
- 📈 When differentiating a square root with an expression inside, apply the chain rule after using the square root differentiation trick.
- 🔄 The second trick involves differentiating a reciprocal of a power function, which can be simplified by flipping the sign, multiplying by the exponent, and adding one to the exponent in the denominator.
- 📉 For the reciprocal differentiation trick, an example is provided where the derivative of \( \frac{1}{x} \) is \( -x^{-2} \), which matches the shortcut method.
- 🔢 The third trick is a method for complex derivatives that would otherwise require multiple applications of the quotient and chain rules.
- ⚡ Logarithmic differentiation is introduced as a powerful tool for simplifying the differentiation of complex functions.
- 📝 Logarithmic differentiation involves taking the natural log of both sides of an equation and applying properties of exponents and logarithms to simplify the process.
- 🌐 The properties of logarithms used include splitting the log of a quotient and expressing the log of a power as the power times the log of the base.
- 📉 After applying logarithmic differentiation, the derivative of both sides of the equation becomes straightforward, using the derivative of the natural logarithm function.
- 🔑 The final step in logarithmic differentiation involves multiplying through by the original function to solve for the derivative, simplifying what would have been a complex process.
- 👍 The video encourages viewers to subscribe for more math tips and tricks, emphasizing the value of these shortcuts in making calculus more manageable.
Q & A
What is the first derivative trick Brian introduces in the video?
-The first derivative trick is a simplified method to find the derivative of a square root function, which is to simply memorize that the derivative of a square root is 1/2 times the square root itself.
How does the power rule for derivatives relate to the first trick mentioned by Brian?
-The power rule for derivatives would typically require writing the square root as x to the 1/2 power and then applying the power rule. Brian's trick bypasses this by directly using 1/2 * the square root as the derivative.
What is the second derivative trick Brian shares, and how does it differ from the traditional method?
-The second trick is for derivatives of a number over x to a power or the reciprocal of x to a power. Instead of using the power rule, Brian suggests flipping the sign, multiplying by the exponent in the denominator, and then adding one to the exponent in the denominator.
Can you provide an example of applying the second trick with a function like 1/(x^7)?
-Applying the second trick to 1/(x^7) involves flipping the sign to positive, multiplying by the exponent 7 to get 42, and then adding one to the exponent in the denominator, resulting in the derivative 42/x^8.
What is the third trick Brian introduces for dealing with complex derivatives?
-The third trick is using logarithmic differentiation in a non-traditional way. Instead of using it for a variable to a variable power, Brian suggests taking the natural log of both sides of a complex equation and applying properties of exponents to simplify the differentiation process.
How does Brian's approach to logarithmic differentiation simplify the derivative of a complex function?
-By taking the natural log of both sides and applying properties of logarithms, Brian simplifies the differentiation process to a straightforward application of the derivative of the natural logarithm, which is much easier than using quotient and chain rules.
What property of logarithms does Brian use to rewrite the log of a quotient?
-Brian uses the property that the log of a quotient can be written as the log of the numerator minus the log of the denominator.
How does Brian apply the property of logarithms for a log to a power in his third trick?
-Brian applies the property that the log of something to a power can be written as the power times the log of the base, which simplifies the differentiation process.
What is the final step Brian takes after differentiating both sides of the equation in his third trick?
-The final step is to multiply both sides of the equation by y to isolate y', which is the derivative of the original function.
Why does Brian recommend memorizing these derivative tricks instead of always using the traditional methods?
-Brian recommends memorizing these tricks because they make the process of finding derivatives much faster and easier, especially when dealing with complex or frequently occurring functions.
What does Brian suggest at the end of the video for viewers who found the tips helpful?
-Brian suggests that viewers who found the tips helpful should subscribe to his channel for more tips and tricks to make their math life easier.
Outlines
📚 Derivative Tricks for Square Roots
In the first paragraph, Brian introduces three derivative tricks that are not commonly taught in class. The focus is on the derivative of a square root function. Traditionally, one would express the square root as x to the power of 1/2 and apply the power rule. However, Brian simplifies this by suggesting a memorized trick: the derivative of a square root is simply 1/2 times the square root itself. He demonstrates this with an example and emphasizes the ease of this method, especially when dealing with more complex expressions inside the square root, by applying the chain rule.
🔄 Reciprocal Power Derivatives and Logarithmic Differentiation
The second paragraph delves into two more derivative tricks. The first trick involves taking the derivative of a number over x to a power or the reciprocal of x to a power. Brian explains a shortcut using the reciprocal rule, which involves flipping the sign, multiplying by the exponent in the denominator, and adding one to the exponent. The second trick is logarithmic differentiation, which is typically used when dealing with variables to variable powers. Brian applies it to a complex derivative problem, taking the natural log of both sides of an equation, applying properties of exponents, and then differentiating both sides. This method simplifies the process significantly compared to using quotient and chain rules.
Mindmap
Keywords
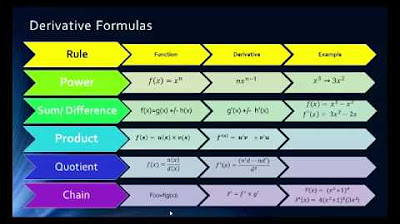
💡Derivative
💡Square Root
💡Power Rule
💡Chain Rule
💡Reciprocal
💡Exponent
💡Logarithmic Differentiation
💡Natural Logarithm
💡Properties of Exponents
💡Quotient Rule
💡Differentiation Tricks
Highlights
Introduction to three derivative tricks not commonly taught in class.
Trick 1: Simplifying the derivative of a square root to 1/2 times the square root.
Explanation of the traditional method of differentiating a square root and its limitations.
Demonstration of the new trick with the derivative of x to the 1/2 power.
Trick 2: Derivatives of a number over x to a power using the reciprocal rule.
The process of flipping the sign, multiplying by the exponent, and adding one to the exponent in the denominator.
Example of applying the reciprocal rule to differentiate 1/x.
Trick 3: Using logarithmic differentiation for complex derivatives.
Explanation of the traditional use of logarithmic differentiation and its limitations.
Demonstration of an alternative approach to logarithmic differentiation for a complex function.
Application of properties of exponents and logarithms in one sweep for differentiation.
Derivation of the derivative using the natural logarithm and properties of logarithms.
Final simplification of the derivative by multiplying both sides by y.
Comparison of the new method to traditional methods like quotient and chain rules.
Conclusion on the efficiency of the three derivative tricks for easier and quicker differentiation.
Encouragement to subscribe for more math tips and tricks.
Closing remarks wishing the viewers a great day.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: