Newton's Second Law | Forces & Motion | Physics | FuseSchool

FuseSchool - Global Education
15 Mar 202004:47
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video delves into Newton's Second Law of Motion, illustrating how force, mass, and acceleration interplay. It uses examples like a thrown ball and a toy car to demonstrate the effects of gravity and unbalanced forces on motion. The video challenges viewers to calculate resultant forces and accelerations in various scenarios, highlighting the relationship between these physical quantities. It concludes with a practical insight into why a tennis ball can be thrown faster than a shot put, due to the difference in mass and resulting acceleration.

Takeaways
  • 🚀 Newton's Second Law of Motion relates force, mass, and acceleration, and is fundamental in understanding how objects move.
  • 🏀 When throwing a ball upwards, the only force acting on it is gravity, which slows it down, stops it, and then accelerates it downwards.
  • 🔗 A ball thrown sideways with a piece of elastic experiences a force from the elastic that slows it and then pulls it back, similar to the effect of gravity on a vertically thrown ball.
  • 🛠 Unbalanced forces can cause objects to speed up, slow down, or change direction, as demonstrated by the example of changing direction on a muddy football field.
  • 🚗 The mass of an object determines the amount of force needed to change its speed or direction, with heavier objects requiring more force.
  • 🔢 Newton's Second Law is mathematically expressed as the equation: resultant force = mass × acceleration, where force is in newtons, mass in kilograms, and acceleration in meters per second squared.
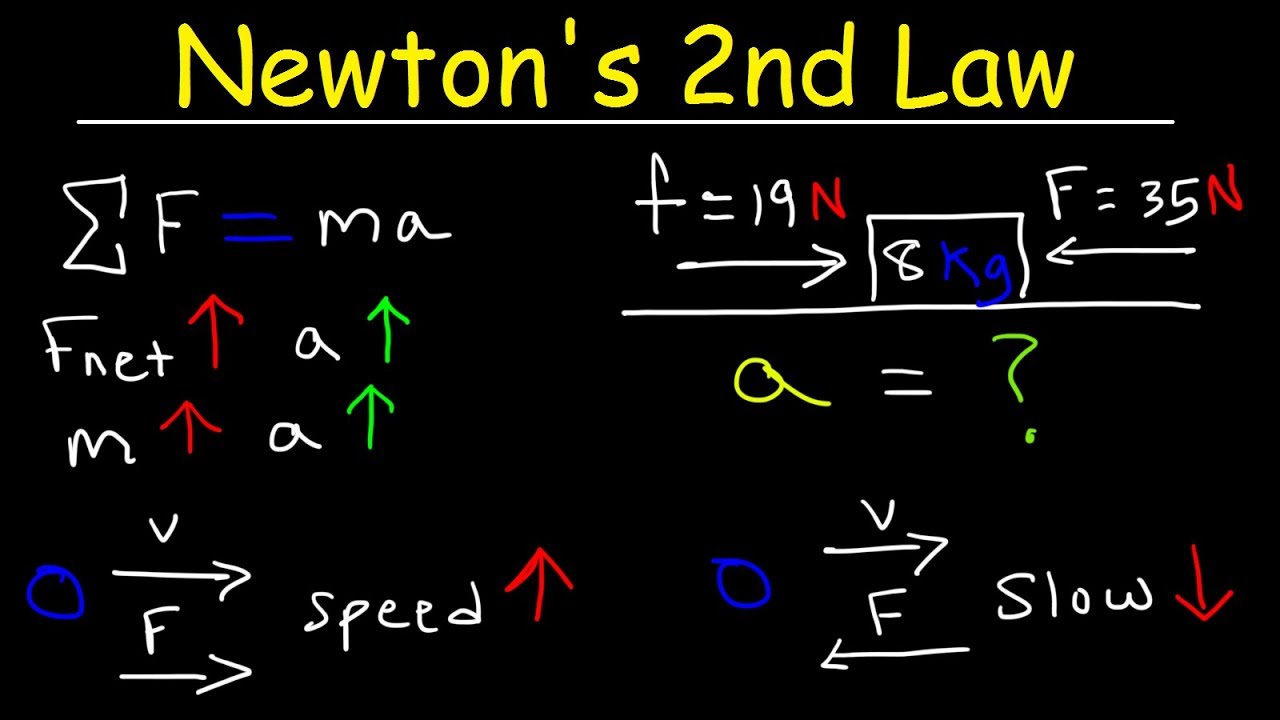
  • 📚 The script provides examples of applying Newton's Second Law to calculate resultant force on a spacecraft and acceleration of a car, emphasizing the importance of unit consistency.
  • 🚀 A spacecraft with a mass of 7150 kg and an acceleration of 2 m/s² can be used to illustrate the calculation of resultant force using Newton's Second Law.
  • 🏎 A car with a mass of 1200 kg and a constant force from the engine, minus the frictional force, can be used to calculate its acceleration.
  • 🧩 The force required to accelerate an object can be calculated if its mass and desired acceleration are known, as shown in the example of an 800-gram toy car.
  • 🎾 The reason why a tennis ball can be thrown faster than a shot put, despite the same force exerted by the arm, is due to the significantly different masses of the two objects.
  • 👍 The video encourages viewers to engage by liking, subscribing, and commenting if they have questions, and also promotes the fusco app for further learning.
Q & A

  • What is Newton's second law of motion?

    -Newton's second law of motion states that the resultant force acting on an object is equal to the mass of the object multiplied by its acceleration, which can be summarized by the equation F = ma, where F is force, m is mass, and a is acceleration.

  • What are the forces acting on a ball thrown upwards, neglecting air resistance?

    -The only force acting on the ball thrown upwards is the downward force of gravity, which slows the ball down, stops it, and then causes it to fall back to the ground.

  • What happens when an object is subjected to an unbalanced force?

    -When an object is subjected to an unbalanced force, it can speed up, slow down, or change direction. The unbalanced force causes a change in the object's velocity.

  • Why does it take more force to change the direction of a heavier object compared to a lighter one?

    -It takes more force to change the direction of a heavier object because the larger mass requires a greater force to alter its state of motion according to Newton's second law of motion.

  • What is the relationship between the force applied to an object and its acceleration?

    -The acceleration of an object is directly proportional to the net force applied to it and inversely proportional to its mass, as described by Newton's second law, F = ma.

  • How can you calculate the resultant force on a spacecraft with a given mass and acceleration?

    -You can calculate the resultant force on a spacecraft by multiplying its mass (in kilograms) by its acceleration (in meters per second squared), using the formula F = ma.

  • What is the difference between the force produced by a car's engine and the frictional force acting on the car?

    -The force produced by a car's engine is the driving force that propels the car forward, while the frictional force is the resistive force that opposes the motion of the car, typically due to the interaction between the tires and the road surface.

  • How do you calculate the acceleration of a car given its mass, the force produced by its engine, and the frictional force acting on it?

    -You can calculate the acceleration of the car by subtracting the frictional force from the engine force and then dividing the result by the car's mass, using the formula a = (F_engine - F_friction) / m.

  • Why can you throw a tennis ball faster than a shot put, even if the force from your arm is the same?

    -You can throw a tennis ball faster than a shot put because the tennis ball has a much smaller mass, and thus, according to Newton's second law, it will experience a greater acceleration for the same applied force.

  • What units are used for force, mass, and acceleration in the equation F = ma?

    -In the equation F = ma, force is measured in newtons (N), mass is measured in kilograms (kg), and acceleration is measured in meters per second squared (m/s²).

  • What is the significance of the mass of an object when calculating the force required to achieve a certain acceleration?

    -The mass of an object is significant because it determines how much force is needed to achieve a certain acceleration. A larger mass requires a greater force to achieve the same acceleration compared to a smaller mass, as per the equation F = ma.

Outlines
00:00
🚀 Newton's Second Law in Action

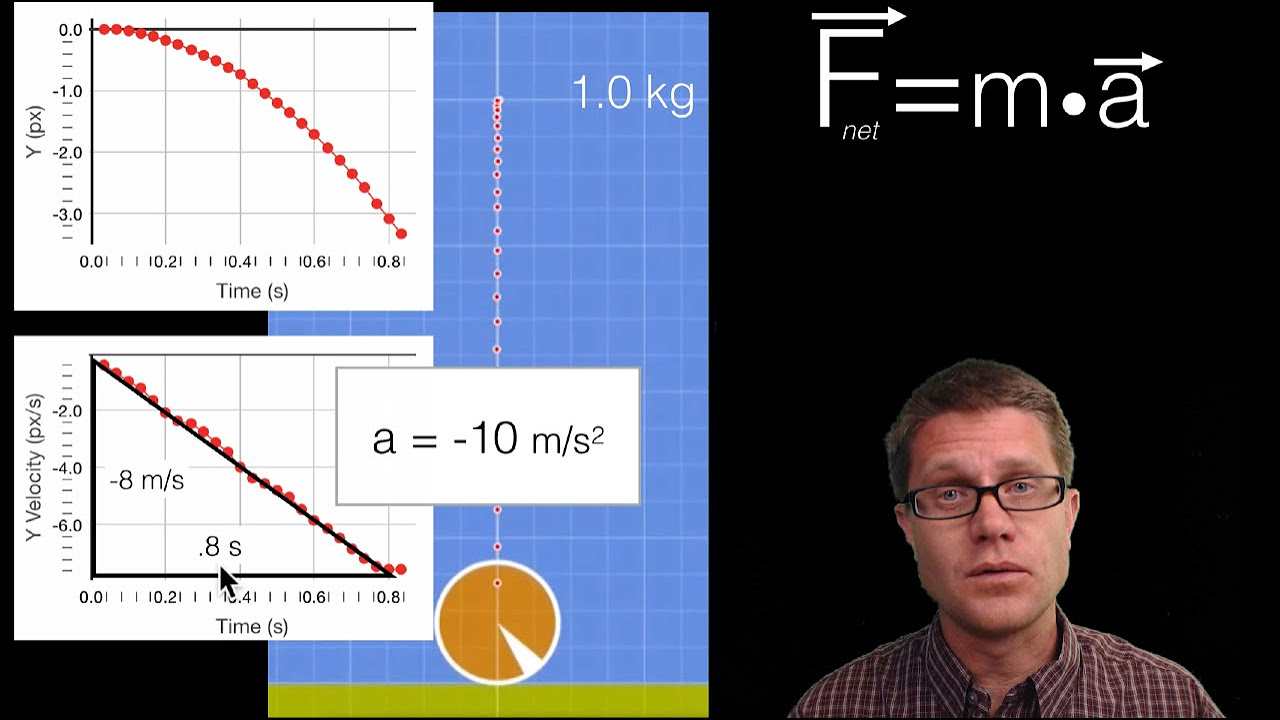
This paragraph introduces Newton's second law of motion, which relates force, mass, and acceleration. It uses the examples of a ball thrown upwards and one attached to a piece of elastic to illustrate how unbalanced forces cause changes in velocity and direction. The paragraph explains that the larger the mass of an object, the greater the force needed to change its speed or direction, and vice versa. It also introduces the formula for Newton's second law: resultant force equals mass times acceleration, with units of newtons for force, kilograms for mass, and meters per second squared for acceleration.

🔢 Practical Applications of Newton's Second Law

This section presents practical examples to apply Newton's second law, including a spacecraft accelerating away from the International Space Station and a car accelerating on a racetrack. It challenges the viewer to calculate the resultant force on the spacecraft and the acceleration of the car, considering both the force produced by the engine and the opposing frictional force. The paragraph also includes a third example calculating the force needed for a toy car to accelerate at a given rate, emphasizing the importance of unit consistency.

🏋️‍♂️ Understanding Force and Mass Relationship

The final paragraph discusses why a tennis ball can be thrown faster than a shot put, despite the same force being applied, due to the difference in mass and resulting acceleration. It concludes with an invitation for viewers to engage with the content by liking the video, subscribing, commenting with questions, and checking out the Fusco app, signaling the end of the video script.

Mindmap
Keywords
💡Newton's Second Law
Newton's Second Law of Motion is a fundamental principle in physics that describes the relationship between force, mass, and acceleration. It states that the force acting on an object is equal to the mass of the object multiplied by its acceleration. In the video, this law is central to understanding how objects like a thrown ball or a spacecraft are affected by forces, with the equation F = ma being used to calculate resultant forces and accelerations.
💡Force
Force is any interaction that, when unopposed, will change the motion of an object. In the context of the video, force is what causes a ball to move upwards initially and then fall back down due to gravity, or what causes a car to accelerate on a racetrack. The video script uses examples of forces such as the force from a hand throwing a ball and the frictional force acting on a moving car.
💡Mass
Mass is a measure of the amount of matter in an object and is typically measured in kilograms. It is a key factor in Newton's Second Law, as the mass of an object determines how it will respond to a given force. The video illustrates this with examples such as the spacecraft with a mass of 7150 kg and a car with a mass of 1200 kg, showing how mass affects the acceleration of objects.
💡Acceleration
Acceleration is the rate of change of velocity of an object with respect to time. It is a vector quantity, meaning it has both magnitude and direction. The video script explains how acceleration occurs when a ball is thrown upwards and slows down due to gravity, or when a car accelerates on a racetrack. The examples given demonstrate how different forces can cause objects to speed up or slow down.
💡Gravity
Gravity is a natural force that attracts two objects with mass towards each other. In the video, gravity is the force that acts on a thrown ball, causing it to slow down, stop, and then fall back to the ground. It is also the force that affects the spacecraft as it moves away from the International Space Station.
💡Unbalanced Force
An unbalanced force occurs when the net force acting on an object is not zero, resulting in a change in the object's motion. The video script describes how an unbalanced force can cause objects to speed up, slow down, or change direction, using the examples of a ball thrown upwards and a car accelerating on a racetrack.
💡Resultant Force
Resultant force is the single force that represents the vector sum of all the forces acting on an object. In the video, the resultant force is calculated to determine the acceleration of a spacecraft or a car, taking into account all the forces acting on them, such as the force produced by an engine and the frictional force.
💡Spacecraft
A spacecraft is a vehicle or machine designed for space travel. In the video, a spacecraft with a specific mass is used as an example to demonstrate the application of Newton's Second Law. The spacecraft's acceleration away from the International Space Station is calculated using the resultant force acting upon it.
💡Frictional Force
Frictional force is the force that opposes the relative motion or tendency of such motion of two surfaces in contact. The video script mentions a constant frictional force acting on a car as it starts moving and accelerates, which is an example of how friction can affect the motion of an object.
💡Tennis Ball vs. Shot Put
The video script uses the comparison between throwing a tennis ball and a shot put to illustrate the concept of mass and acceleration. Despite the same force being applied by the arm, the tennis ball, having a smaller mass, will accelerate more than the shot put, which has a larger mass, resulting in the ball being thrown faster.
Highlights

Introduction to Newton's second law of motion and its application in calculations involving force, mass, and acceleration.

Explanation of the forces acting on a ball thrown upwards, emphasizing the unbalanced force of gravity.

Illustration of how unbalanced forces can cause objects to speed up, slow down, or change direction.

Comparison of the effects of unbalanced forces on a ball thrown upwards versus one pulled by an elastic band.

Discussion on the relationship between mass and the force required to change an object's speed or direction.

Introduction of Newton's second law equation: resultant force equals mass times acceleration.

Example calculation of the resultant force on a spacecraft accelerating away from the International Space Station.

Challenge for viewers to calculate the spacecraft's resultant force, encouraging active learning.

Example involving a car's acceleration on a racetrack with given mass, engine force, and frictional force.

Instruction for viewers to calculate the car's acceleration, fostering problem-solving skills.

Calculation of the force needed to accelerate an 800-gram toy car at a specific rate, emphasizing unit consistency.

Explanation of why a tennis ball can be thrown faster than a shot put, despite the same force applied.

Encouragement for viewers to like, subscribe, and comment if they have questions, promoting engagement.

Promotion of the Fusco app as a resource for further learning.

Conclusion and sign-off for the video, inviting viewers to look forward to the next session.

Transcripts

Browse More Related Video

Newton's Second Law of Motion | Newton's Laws of Motion | Video for Kids

Newton's Law of Motion - First, Second & Third - Physics

Newton's First Law of Motion | Newton's Laws of Motion | Video for Kids

Physics - Basic Introduction

Newton's Second Law of Motion - Force, Mass, & Acceleration

Newton's Second Law

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Newton's LawPhysicsForceMassAccelerationEducationalMotionSpacecraftCar DynamicsToy CarScience