Calculus AB/BC – 1.10 Exploring Types of Discontinuities
TLDRIn this educational video, Mr. Bean teaches the fundamentals of continuity and discontinuities in calculus. He introduces the concept of a continuous function as one that can be drawn without lifting the pen, contrasting it with discontinuous functions that require lifting the pen. Mr. Bean categorizes discontinuities into three types: removable (holes), non-removable due to vertical asymptotes, and jump discontinuities, focusing on the first two in this lesson. He explains how to identify discontinuities by looking for when the denominator of a fraction equals zero, and demonstrates this with various examples, including trigonometric functions and polynomial expressions, providing a clear and engaging explanation suitable for all learning levels.
Takeaways
- 📚 The lesson is about understanding continuity and discontinuities in calculus.
- 🖊 Continuity is defined by the ability to draw a function without lifting the pen, while discontinuities occur when the pen must be lifted.
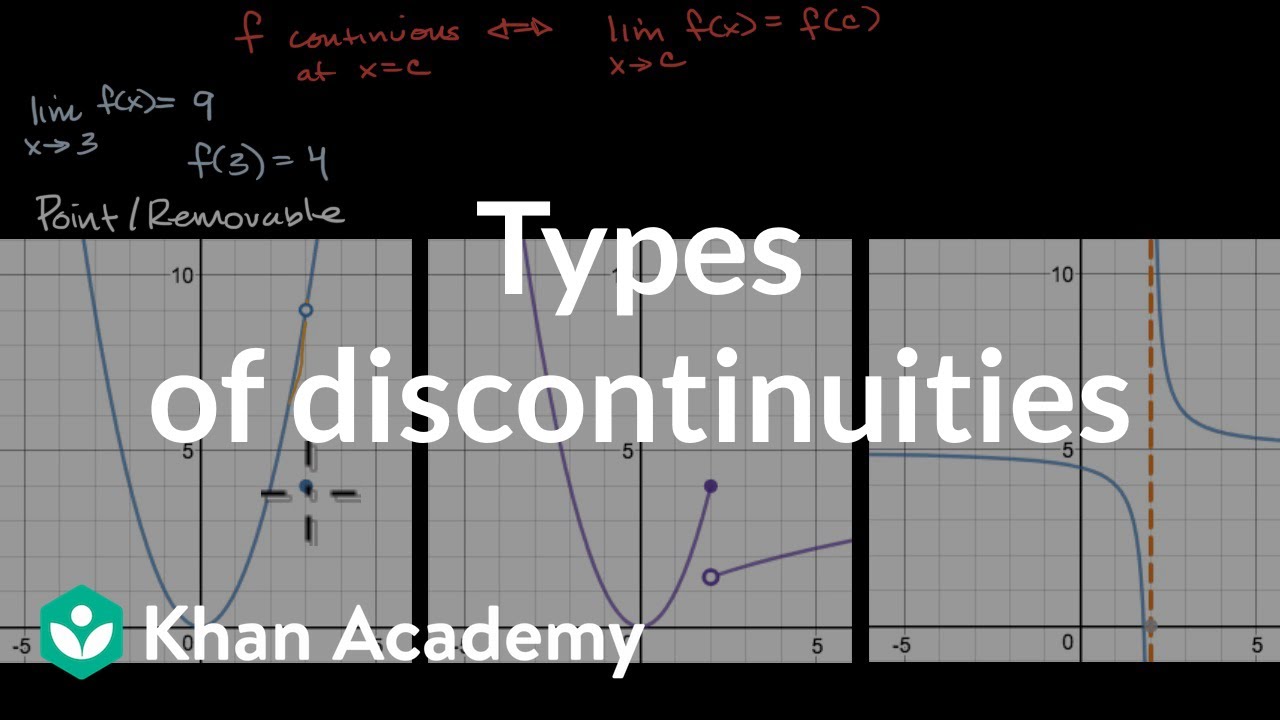
- 🕳 The first type of discontinuity discussed is a 'hole', which is considered removable as it can be filled in to restore continuity.
- 📉 The second type is a discontinuity due to a vertical asymptote, which is non-removable because it cannot be fixed by filling in a point.
- 🔄 The third type, a jump discontinuity, is usually associated with piecewise functions and is also non-removable.
- 🔍 To identify discontinuities, one should look for fractions where the denominator equals zero, as division by zero is undefined.
- 🔢 Factoring the numerator and denominator of a fraction can help determine if there are removable discontinuities (holes) or non-removable ones (vertical asymptotes).
- 📐 For trigonometric functions, the discontinuities occur when the denominator, often a trigonometric function itself, equals zero.
- 🌀 When dealing with trigonometric functions, remember that cosine equals zero at the top and bottom of the unit circle, which corresponds to specific angles.
- ⏲ The lesson packet and practice problems will focus on removable and non-removable discontinuities, with jump discontinuities and a formal definition of continuity covered in the next lesson.
- 📈 For a function like x squared minus one, if it's a continuous function with no denominators to worry about, there are no discontinuities.
Q & A
What is the basic concept of continuity in a function according to Mr. Bean's explanation?
-A function is considered continuous if you can draw it without having to lift your pen or pencil off the paper.
What is the difference between a removable discontinuity and a non-removable discontinuity?
-A removable discontinuity, often represented as a hole in the graph, can be fixed by filling in the hole, making the graph continuous. A non-removable discontinuity, such as a vertical asymptote, cannot be fixed by simply filling in a point.
What is the significance of a denominator being equal to zero in the context of discontinuities?
-A denominator being equal to zero indicates a discontinuity because division by zero is undefined, and thus the function cannot be graphed at that point.
How does Mr. Bean suggest identifying discontinuities in a function involving fractions?
-Mr. Bean suggests factoring both the numerator and the denominator. If the factor in the denominator does not cancel out with any factor in the numerator, it represents a discontinuity.
What is a hole in a graph and why is it considered a removable discontinuity?
-A hole in a graph is a point where the function is not defined, but it is considered a removable discontinuity because filling in the hole with a defined value would make the graph continuous at that point.
Can you have a discontinuity at a point where the numerator equals zero if the denominator is not zero?
-No, a discontinuity occurs when the denominator equals zero, not the numerator. If the numerator is zero and the denominator is not, the function is defined at that point.
What is a vertical asymptote and why is it a non-removable discontinuity?
-A vertical asymptote is a line that the graph approaches but never crosses, often occurring at points where the denominator of a fraction is zero. It is a non-removable discontinuity because it represents an undefined point in the function that cannot be fixed by simply filling in a value.
How does Mr. Bean illustrate the concept of cosine being equal to zero using the unit circle?
-Mr. Bean uses the unit circle to show that cosine is equal to zero at the top and bottom of the circle, corresponding to angles of PI/2, 3PI/2, 5PI/2, etc., where PI represents the mathematical constant pi.
What is the range of x values that Mr. Bean suggests focusing on when dealing with the discontinuities of the function involving sine and cosine?
-Mr. Bean suggests focusing on the range of x values from 0 to 2 pi when dealing with discontinuities in the function involving sine and cosine.
What does Mr. Bean mean by saying 'jump discontinuity' and why is it not the focus of the current lesson?
-A jump discontinuity occurs at a point where the function has different one-sided limits. It is not the focus of the current lesson because Mr. Bean plans to cover it in the next lesson, along with a formal definition of continuity.
Why would a function like 'x squared minus one' be considered continuous?
-The function 'x squared minus one' is a parabola and is considered continuous because it does not have any points where the function is undefined or where the graph has breaks, holes, or vertical asymptotes.
Outlines
📚 Introduction to Continuity and Discontinuities
In this educational video, Mr. Bean introduces the concept of continuity and discontinuities in calculus. He explains that a function is considered continuous if it can be drawn without lifting the pen, and discontinuous if the pen must be lifted. The types of discontinuities discussed include 'holes' which are removable, vertical asymptotes which are non-removable, and jump discontinuities which will be covered in a future lesson. Mr. Bean emphasizes the importance of understanding when a function has a discontinuity, which typically occurs when the denominator of a fraction is zero, as division by zero is undefined. He provides a step-by-step example of how to identify discontinuities by factoring the numerator and denominator and determining where the denominator equals zero, which indicates the presence of a hole or a vertical asymptote.
🔍 Analyzing Discontinuities in Trigonometric Functions
This paragraph delves deeper into identifying discontinuities within trigonometric functions, specifically focusing on the tangent function. The instructor demonstrates how to rewrite the tangent function to reveal its denominator and then identifies when the cosine function equals zero, which is crucial for determining the discontinuities. By using the unit circle, Mr. Bean illustrates the points where cosine is zero and translates these to the context of the given function, sine of 2x over cosine of 2x. He explains the process of solving for x when the cosine of 2x equals zero and identifies the specific x-values that correspond to vertical asymptotes within the restricted range of 0 to 2π. The summary clarifies the method of solving and the importance of checking the range of x-values to ensure they are relevant to the problem.
📉 Discontinuities in Polynomial and Trigonometric Functions
The final paragraph of the script covers the identification of discontinuities in a polynomial function and a trigonometric function. The instructor provides a straightforward example of a parabola, x squared minus one, which is continuous and has no discontinuities. He contrasts this with the previous examples, emphasizing that in some cases, functions may not have any discontinuities at all. The summary highlights the importance of recognizing when a function is continuous and how to articulate this in the context of finding discontinuities, suggesting that one can state 'continuous function' or 'no discontinuities' when applicable.
Mindmap
Keywords
💡Continuity
💡Discontinuities
💡Hole
💡Removable Discontinuity
💡Vertical Asymptote
💡Non-Removable Discontinuity
💡Jump Discontinuity
💡Denominator
💡Factoring
💡Trig Functions
💡Unit Circle
💡Continuous Function
Highlights
Introduction to the concept of continuity and discontinuities in calculus.
Explanation of a continuous function as one that can be drawn without lifting the pen.
Differentiation between a removable discontinuity, represented by a hole in the graph, and non-removable discontinuities.
Identification of a hole as a removable discontinuity that can be fixed by filling in the gap.
Vertical asymptotes as non-removable discontinuities that cannot be fixed by adding a single point.
Jump discontinuities associated with piecewise functions that break the graph.
Focus on fractions in functions and the importance of avoiding a zero denominator.
Method to find discontinuities by factoring the numerator and denominator of a fraction.
Explanation of how to determine if a discontinuity is a hole or a vertical asymptote based on factor cancellation.
Remind that a hole is a removable discontinuity, unlike a vertical asymptote.
Introduction of trigonometric functions and their relation to finding discontinuities.
Use of the unit circle to determine when cosine equals zero, indicating potential discontinuities.
Process of solving for x when the trigonometric function's denominator equals zero.
Identification of vertical asymptotes in trigonometric functions by solving the equation.
Clarification on the exclusion of imaginary numbers when dealing with discontinuities in real functions.
Demonstration of a function with no discontinuities, such as a simple parabola.
Instruction on how to respond when a function is continuous and no discontinuities are present.
Transcripts
Browse More Related Video

AP Calculus AB - 1.10 Exploring Types of Discontinuities

BusCalc 01 Continuity and Discontinuities
Types of discontinuities | Limits and continuity | AP Calculus AB | Khan Academy

Calculus AB/BC – 1.13 Removing Discontinuities

Three Types of Discontinuities in Functions

Calculus 1 Lecture 1.4: Continuity of Functions
5.0 / 5 (0 votes)
Thanks for rating: