Integrals AKA Antiderivatives EXPLAINED with Examples

Ace Tutors
24 Oct 202004:03
EducationalLearning
32 Likes 10 Comments

TLDRThis video delves into the concept of integrals in calculus, following the study of derivatives. It explains integrals as the reverse process of differentiation, using the integral symbol and 'dx' to denote the antiderivative of a function. The video clarifies that while the derivative of x cubed is 3x squared, the antiderivative must account for a possible constant, leading to the general form x cubed plus C. The presenter emphasizes the importance of verifying answers by applying the reverse operation, highlighting the relationship between derivatives and integrals as inverse processes. The video concludes with a teaser for future content on definite integrals and solution techniques, encouraging viewers to subscribe for more educational insights.

Takeaways
  • 📚 Integrals are the next common topic in calculus after derivatives.
  • 🔍 To find integrals, you work backwards from derivatives to find the original function.
  • ➡️ Derivatives and integrals are opposite operations, like subtraction is to addition or division is to multiplication.
  • 📝 The integral notation is represented by an elongated S with 'dx' at the end, representing the function to be integrated.
  • 🔑 When finding the integral, you must consider the possibility of an additional constant in the original function.
  • 💡 The integral of a derivative often includes an arbitrary constant 'C' to account for any constant that might have been in the original function.
  • 📉 The integral of 3x squared is x cubed plus C, which includes the arbitrary constant.
  • 🔄 Learning derivatives first allows you to verify integrals by taking the derivative of your integral to see if it returns the original function.
  • 📈 The video mentions that there are different types of integrals, including indefinite and definite integrals, with techniques for solving them to be covered in future videos.
  • 👍 The video encourages viewers to subscribe for more helpful content and reminds them to pursue their big dreams despite academic challenges.
Q & A

  • What is the main topic of this video?

    -The main topic of this video is integrals in calculus, explaining what they are and why they are needed.

  • What is the relationship between derivatives and integrals?

    -Derivatives and integrals are opposite operations. While derivatives work forward to find the rate of change, integrals work backward to find the original function from its derivative.

  • What is the notation used to represent an integral?

    -The notation used to represent an integral is the curly elongated S-leg symbol with 'dx' at the end, followed by the function for which the antiderivative is being found.

  • Why do we need to add a constant 'C' when finding the antiderivative of a function?

    -We add a constant 'C' to account for the possibility that the original function had an additional constant when its derivative was taken.

  • What is the antiderivative of the derivative of x cubed?

    -The antiderivative of the derivative of x cubed is x cubed plus an arbitrary constant C.

  • How can you verify if your antiderivative is correct?

    -You can verify if your antiderivative is correct by taking the derivative of your antiderivative and checking if it gives you back the original function.

  • What is the term for the integral that includes an arbitrary constant C?

    -The integral that includes an arbitrary constant C is known as an indefinite integral.

  • What is the difference between indefinite and definite integrals?

    -The video does not provide a direct answer to this question, but it mentions that definite integrals and techniques for solving them will be covered in a future video.

  • What is the purpose of the 'dx' in the integral notation?

    -The 'dx' in the integral notation represents the differential element, indicating that the integration is being performed with respect to the variable x.

  • Why is it important to learn derivatives before integrals?

    -Learning derivatives first is beneficial because it allows you to verify the correctness of your integrals by taking the derivative of the antiderivative and checking if it matches the original function.

  • What does the video suggest for further learning?

    -The video suggests that there will be a future video covering definite integrals and techniques for solving both indefinite and definite integrals.

Outlines
00:00
📚 Introduction to Integrals in Calculus

This paragraph introduces the concept of integrals as the next topic following derivatives in the study of calculus. It explains that integrals, or antiderivatives, are the inverse operation of derivatives. The video aims to clarify what integrals are and their necessity in mathematical analysis. The explanation begins by revisiting the concept of derivatives, using the power rule for the function x cubed as an example. It then contrasts derivatives with integrals, emphasizing that while derivatives work forwards to find rates of change, integrals work backwards to find the original function from its derivative. The integral notation is introduced, which includes the integral symbol followed by 'dx' and the function to be integrated. The paragraph also discusses the inclusion of an arbitrary constant 'C' when finding antiderivatives to account for the possibility of the original function having an additional constant term. The process of verifying the correctness of an antiderivative by taking its derivative to retrieve the original function is highlighted. The video promises to cover definite integrals and solution techniques in future content.

Mindmap
Keywords
💡Derivatives
Derivatives in calculus refer to the rate at which a function changes with respect to its variable. They are a fundamental concept in the field of mathematics, used to describe the instantaneous change of one quantity relative to another. In the video, derivatives are initially discussed to contrast with integrals, showing how they are inverse operations. For example, the derivative of x cubed is calculated using the power rule, resulting in 3x squared.
💡Integrals
Integrals are the mathematical operation that is the inverse of differentiation. They are used to find the accumulated change of a function over an interval and are represented by the integral symbol ∫ with a function and 'dx' underneath. The video explains that integrals are the focus after derivatives and are used to find the original function from its derivative, which is key to understanding the concept of antiderivatives.
💡Antiderivatives
Antiderivatives, also known as indefinite integrals, are functions that represent the reverse process of differentiation. They are the functions that, when differentiated, yield the original function. The video script illustrates this by explaining that finding the antiderivative of 3x squared would lead us back to x cubed, plus an arbitrary constant 'C'.
💡Power Rule
The power rule is a basic principle in calculus used to find the derivative of a function that is a polynomial. It states that the derivative of x raised to the power of n (where n is a constant) is n times x to the power of n-1. In the video, the power rule is used to find the derivative of x cubed, which is 3x squared.
💡Arbitrary Constant (C)
In the context of antiderivatives, an arbitrary constant 'C' is added to account for the fact that the derivative of a constant is zero. This means that when finding the antiderivative, the original function could have had a constant term, which is not reflected in its derivative. The video mentions adding 'C' to x cubed when finding the antiderivative of 3x squared to represent this unknown constant.
💡Indefinite Integral
An indefinite integral represents the family of all antiderivatives of a given function. It is denoted by the integral symbol without specifying the limits of integration. The video introduces the concept of indefinite integrals and contrasts them with definite integrals, which will be covered in a future video. The indefinite integral of 3x squared is given as x cubed plus C in the script.
💡Definite Integral
A definite integral is a specific type of integral that calculates the accumulated change (or net area) of a function over a specified interval. It is represented by the integral symbol with limits of integration. Although not fully explained in the script, the video mentions that definite integrals will be covered in a future video, indicating that they are an important concept in calculus.
💡Inverse Operations
Inverse operations are mathematical operations that 'undo' each other. In the context of calculus, differentiation and integration are inverse operations. The video script emphasizes this by stating that just as addition and subtraction or multiplication and division are opposites, so are derivatives and integrals.
💡Function
A function in mathematics is a relation between a set of inputs and a set of permissible outputs, with the property that each input is related to exactly one output. The video discusses functions in the context of derivatives and integrals, using the function x cubed as an example to illustrate the process of finding derivatives and antiderivatives.
💡Verification
Verification in calculus involves checking the correctness of a solution, often by applying inverse operations. The video script suggests using the process of differentiation to verify the correctness of an antiderivative. For instance, differentiating x cubed plus C should yield the original derivative, 3x squared, thus confirming the antiderivative is correct.
Highlights

Introduction to integrals as the next topic following derivatives in calculus.

Relating integrals to derivatives as inverse operations.

Explanation of the integral notation with the elongated S symbol and dx.

Finding the antiderivative of a function as the reverse process of taking a derivative.

The concept that the derivative of x cubed is 3x squared.

The realization that the derivative of x cubed plus a constant remains 3x squared.

The necessity to include a potential constant when finding the antiderivative.

The representation of the unknown constant as 'C' in the antiderivative.

Verification of an antiderivative by taking its derivative to check for the original function.

The integral of 3x squared being x cubed plus C.

The concept of indefinite integrals versus definite integrals.

Future coverage of definite integrals and solving techniques in upcoming videos.

Encouragement to verify answers by using the inverse relationship between derivatives and integrals.

The importance of learning derivatives first to facilitate the understanding of integrals.

Invitation to subscribe for more helpful content on calculus.

Closing motivational message about pursuing big dreams despite academic challenges.

Transcripts

Browse More Related Video

Calculus - Lesson 16 | Indefinite and Definite Integrals | Don't Memorise

Antiderivatives and indefinite integrals | AP Calculus AB | Khan Academy

The Indefinite Integral or Anti-derivative

What's an anti-derivative?

AP Calculus AB Crash Course Day 5 - Integration and Differential Equations

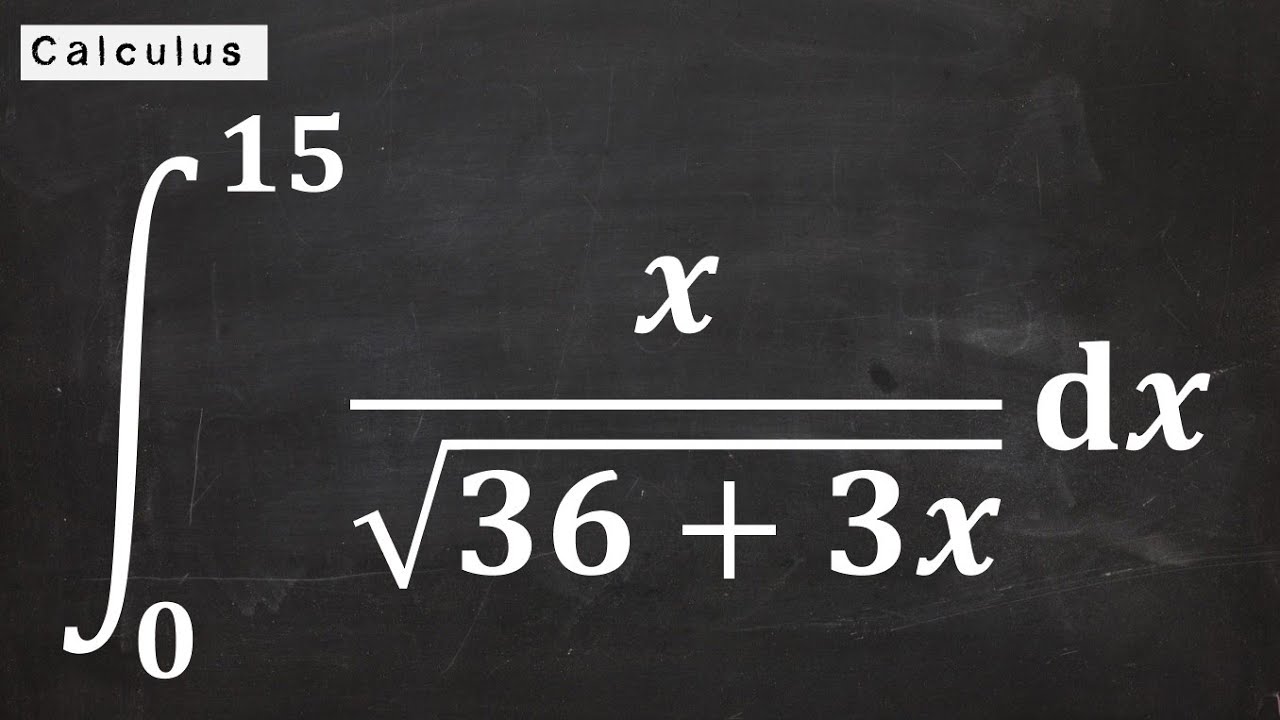
Definite Integral With U-Substitution

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
IntegralsDerivativesCalculusAntiderivativesPower RuleMathematicsEducationalLearningMath HelpEducation Channel