Lecture 03: Another Car, Another Crime The Second Idea of Calculus The Integral
TLDRThis calculus lecture introduces the integral, the second fundamental concept after the derivative. The professor uses a crime-themed scenario involving a kidnapped agent observing a speedometer from inside a moving van to illustrate the concept. The integral is explained through estimating distance traveled by analyzing the speed over time, starting with simple cases like constant speed and moving to more complex scenarios involving variable speeds. The lecture demonstrates how to approximate distance using both overestimations and underestimations, narrowing down to the actual distance traveled through finer time intervals. The integral is presented as the limit of these approximations as the time intervals become infinitesimally small, highlighting calculus's power to transform complex processes into simple formulas.
Takeaways
- 🚗 The script introduces the integral, the second fundamental concept of calculus, which is used to calculate the distance traveled by a moving object when only its instantaneous velocity is known.
- 🔍 The integral is explained through a hypothetical scenario involving a kidnapped agent who records the speed of a van via a video camera, aiming to deduce the distance traveled based on the speedometer readings.
- 📚 The lecture emphasizes that the integral involves an infinite process and is a natural result of analyzing motion, similar to how the derivative was introduced to address Zeno's paradoxes of motion.
- 📉 The concept of a step function is used to simplify the calculation of distance when the velocity changes in discrete steps, allowing for easy computation of total distance traveled.
- 🔢 The strategy for calculating distance with non-constant velocities involves breaking the time into smaller intervals and summing the products of velocity and time for each interval, refining the estimate by making the intervals smaller.
- 📈 The script illustrates the process of underestimating and overestimating distance traveled to sandwich the actual distance between two values, improving the estimate by using finer time intervals.
- 🔬 The integral is conceptualized as a limiting process, where taking increasingly smaller time intervals (delta t) leads to a more accurate approximation of the total distance traveled.
- 📝 The integral is defined as the sum of an infinite series of products of velocity at time t and an infinitesimally small time interval, which converges to the exact distance traveled as the interval approaches zero.
- 🔄 The script highlights the iterative nature of calculus, where understanding simple cases leads to solving more complex ones, and the importance of patterns in simplifying calculations.
- 🔑 The power of calculus is demonstrated through the ability to derive formulas, such as the relationship between time and distance traveled (distance = time squared in the given example), which can instantly provide answers to complex problems.
Q & A
What are the two fundamental concepts of calculus introduced in the lectures?
-The two fundamental concepts of calculus introduced in the lectures are the derivative and the integral. The derivative is related to the instantaneous velocity of a moving object, while the integral is associated with calculating the distance traveled by an object given its velocity function over time.
How does the concept of the derivative help in resolving Zeno's paradoxes of motion?
-The derivative helps in resolving Zeno's paradoxes of motion by providing a mathematical way to define instantaneous velocity. It allows us to understand the velocity of an object at any given moment, thus avoiding the mistake of dividing zero by zero and settling the idea of continuous motion despite the infinitely divisible nature of time and space.
In the context of the lecture, what crime scenario is used to introduce the integral?
-The crime scenario used to introduce the integral is a kidnapping case where the victim is held in the back of a van and can only see the speedometer through a small hole. The challenge is to determine the distance traveled based on the recorded speedometer readings over an hour.
What is the significance of the speedometer in the kidnapping scenario?
-The speedometer is significant in the kidnapping scenario because it is the only source of information about the van's motion. The victim uses it to record the velocity at different times, which is later used to calculate the total distance traveled and help determine the location on the road.
How does the lecturer simplify the problem of calculating distance traveled when the velocity is constant?
-When the velocity is constant, the lecturer simplifies the problem by multiplying the constant velocity by the elapsed time. This direct multiplication gives the total distance traveled without the need for complex calculations.
What is a step function in the context of the lecture?
-In the context of the lecture, a step function represents a velocity function where the speed remains constant for a certain interval of time and then instantly jumps to another constant value for the next interval, creating a 'step' effect on the graph.
How does the strategy of using an 'underestimate' and an 'overestimate' help in finding the actual distance traveled?
-The strategy of using an 'underestimate' and an 'overestimate' helps in finding the actual distance traveled by providing bounds within which the true value must lie. By considering a car that moves at the lowest and highest velocities attained during each interval, we can ensure that the actual distance is between these two values, allowing for a more accurate approximation.
What is the concept of 'delta t' in the context of the integral?
-In the context of the integral, 'delta t' represents a very small increment of time. The integral is computed by breaking down the time interval into very fine increments of 'delta t', calculating the distance for each small interval, and then taking the limit as 'delta t' approaches zero to find the exact distance traveled.
How does the integral help in finding the total distance traveled by a car when the velocity is not constant?
-The integral helps in finding the total distance traveled by a car when the velocity is not constant by summing up the products of the velocity at each small interval of time (delta t) and the interval itself. As the intervals become smaller, the approximation becomes more accurate, and in the limit, it gives the exact total distance traveled.
What is the fundamental theorem of calculus and why is it significant?
-The fundamental theorem of calculus is not explicitly defined in the script, but it is hinted to establish the connection between the derivative and the integral. It is significant because it shows that these two concepts are inverse processes of one another, allowing for the computation of derivatives and integrals in a unified framework.
Outlines
🚗 Introduction to Calculus and the Integral Concept
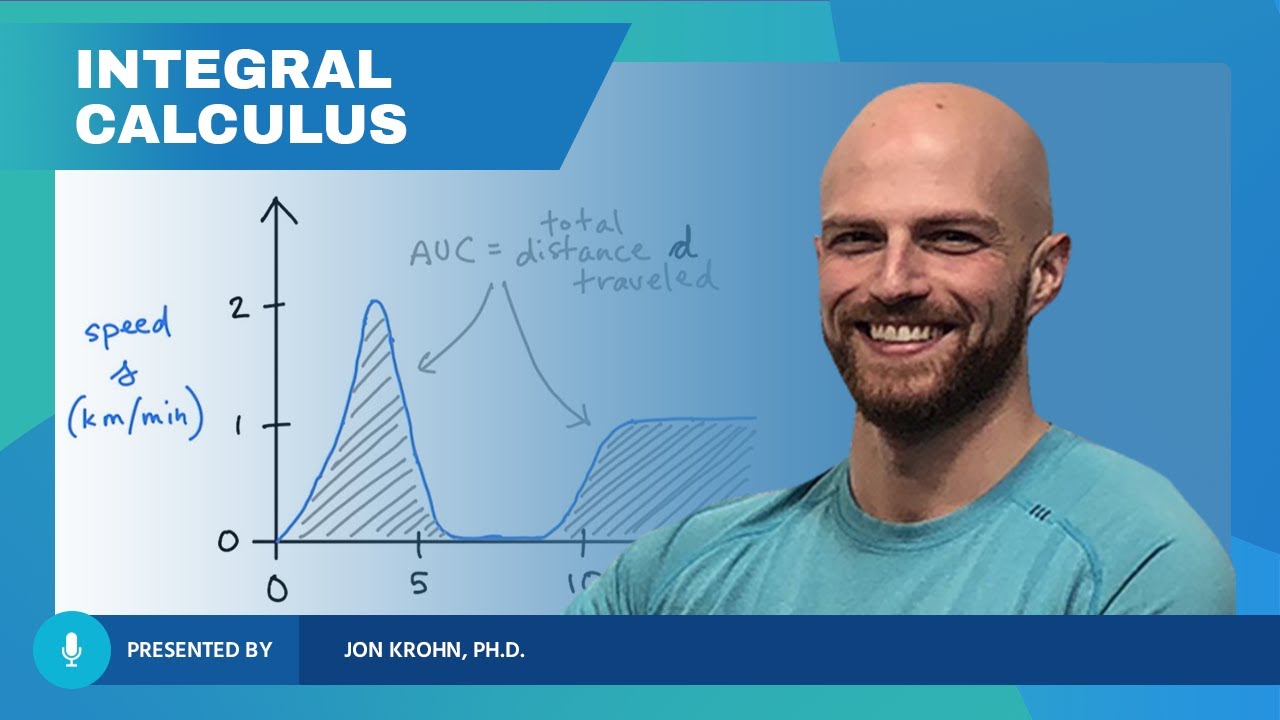
This paragraph introduces the second fundamental concept of calculus, the integral, which is presented as a natural extension of analyzing motion, specifically the distance traveled by a vehicle. The scenario involves a kidnapping where the victim, an agent, is confined in a van and can only see the speedometer through a small hole. The challenge is to determine the distance traveled based on a video recording of the speedometer's readings over an hour. The integral is introduced as the strategy to deduce distance from the speedometer's data, which is a new way to approach problems involving infinite processes.
📊 Understanding Constant Velocity and the Simplest Case of Integration
The speaker explains how to calculate the distance traveled when the vehicle's velocity is constant. By multiplying the constant velocity (speed) by the time elapsed, the total distance can be easily determined. This simple case serves as a foundation for understanding more complex scenarios where the velocity changes over time. The example given is a car traveling at one mile per minute for a full hour, resulting in a straightforward calculation of 60 miles traveled.
🔍 Dealing with Variable Velocity: The Step Function Approach
The paragraph explores the scenario where the car's velocity changes abruptly at fixed time intervals, creating a step function of velocity over time. The strategy involves calculating the distance for each time interval where the velocity is constant and then summing these distances to find the total distance traveled over the hour. The example provided increases the velocity by one mile per minute every ten minutes, resulting in a total distance calculation of 210 miles after one hour.
📈 Estimating Distance with Non-constant Velocity: The Riemann Sum
The discussion moves to a more complex situation where the car's velocity changes smoothly over time. The strategy now involves approximating the distance traveled by considering the velocity at specific intervals and assuming constant velocity within each interval. The example given is a velocity function that doubles with each minute, starting from zero. The speaker describes an approach to underestimate and overestimate the distance traveled to bracket the actual distance, using the concept of Riemann sums.
🔧 Refining the Estimate: Narrowing the Sandwich of Over and Under Estimates
To improve the accuracy of the distance estimate, the speaker suggests using smaller time intervals. By dividing the total time into tenths of a minute and applying the same over and underestimate strategy, the speaker demonstrates how to narrow the range within which the actual distance traveled must lie. This approach refines the approximation, bringing the underestimate and overestimate closer together, and providing a more precise estimate of the car's distance traveled.
🌟 The Concept of Limits and the Fundamental Nature of the Integral
The integral is defined as the limit of the Riemann sum as the size of the time intervals (delta t) approaches zero. The speaker explains that the exact distance traveled is found by performing an infinite number of additions, each time with a smaller delta t, which is a central concept in calculus. The integral is presented as the process of dividing the time interval into small increments, multiplying the velocity by these increments, and taking the limit as the increments become infinitesimally small.
🔗 The Integral and the Pattern in Motion: Squared Time Equals Distance
The speaker concludes by identifying a pattern in the distance traveled over time for the specific velocity function given (velocity equals two times time). It is observed that the distance traveled is the square of the time elapsed. This pattern allows for the formulation of a simple formula to calculate the distance traveled at any given time, demonstrating the power of calculus to transform a complex, iterative process into a straightforward calculation.
🛣️ The Integral in Action: Computing Distance from Velocity Function
The final paragraph summarizes the integral's role in calculating the net distance traveled by a car given its velocity function over a specific time interval. The integral is presented as the accumulation of infinitesimally small distances, each computed by multiplying the velocity at a given instant by an infinitesimally small time increment (delta t). The process of taking the limit as delta t approaches zero yields the exact distance traveled, illustrating the integral's application in real-world problems.
🔍 Looking Forward to the Fundamental Theorem of Calculus
The speaker anticipates the next lecture, where the connection between the derivative and the integral will be explored. The fundamental theorem of calculus, which establishes the inverse relationship between these two concepts, will be the focus of the upcoming session, promising to further bridge the understanding of these foundational calculus tools.
Mindmap
Keywords
💡Derivative
💡Integral
💡Zeno's Paradoxes
💡Instantaneous Velocity
💡Speedometer
💡Kidnapping Scenario
💡Step Function
💡Velocity Function
💡Overestimate and Underestimate
💡Limiting Process
💡Fundamental Theorem of Calculus
Highlights
Introduction of the integral as the second fundamental concept of calculus.
The integral is related to an infinite process and analyzing the motion of a vehicle.
A scenario involving a kidnapping and the use of a speedometer to deduce distance traveled.
The strategy of using a video recording of the speedometer to calculate the car's position.
Exploring the simple case of constant velocity and its straightforward calculation for distance.
The concept of multiplying velocity by time to get distance when velocity is constant.
Analyzing a more complex case with non-constant velocity and instantaneous changes.
Computing distance with a step function representing velocity changes over time.
The strategy of adding distances traveled during each time interval for non-constant velocity.
Dealing with real-life scenarios where velocity smoothly changes over time.
Using an underestimate and overestimate strategy to find the actual distance traveled.
Graphical representation of velocity and the strategy of comparing it with a 'jerky' car's motion.
The idea of refining estimates by taking smaller time intervals (delta t).
The integral as a process of infinitely many additions to find the exact distance traveled.
The integral's connection to the concept of limits in calculus.
The fundamental theorem of calculus to be discussed in the next lecture as a connection between derivatives and integrals.
The integral's definition as the limit of a sum of products of velocity and small time intervals.
Transcripts
Browse More Related Video

Definite integrals (part II)
Calculus -- The foundation of modern science

Rotational Motion - Merry Go Round Slowing Down | Physics with Professor Matt Anderson | M12-03

Business Calculus - Math 1329 - Sections 5.4 & 5.5 - Applications of the Definite Integral

Area under rate function gives the net change | AP Calculus AB | Khan Academy
What Integral Calculus Is — Topic 85 of Machine Learning Foundations
5.0 / 5 (0 votes)
Thanks for rating: