College Physics 1: Lecture 15 - Equilibrium and Newton's Second Law
TLDRThis lecture on 'Equilibrium and Newton's Laws' delves into applying Newton's second law (F=ma) to solve problems involving equilibrium states, where objects are either at rest or moving at a constant speed in a straight line. The instructor explains that in equilibrium, the net force and acceleration are zero, leading to a sum of forces equaling zero. The lecture progresses through examples, starting with a simple scenario of an orangutan hanging from a rope, moving to a car being towed with friction, and concluding with a ball pulled by a rope at an angle. Each example illustrates the importance of identifying forces, drawing free body diagrams, and using Newton's laws to calculate tensions. The session aims to prepare students for solving more complex problems involving non-equilibrium states in future lectures.
Takeaways
- 📚 Newton's First Law states that an object at rest stays at rest, and an object in motion stays in motion with the same speed and in a straight line unless acted upon by an unbalanced force.
- 📐 Newton's Second Law is mathematically formulated as F = m*a, where F is the force applied, m is the mass of the object, and a is the acceleration.
- ⚖️ Newton's Third Law asserts that for every action, there is an equal and opposite reaction, meaning forces always occur in pairs that are equal in magnitude and opposite in direction.
- ⚖️ Equilibrium refers to a state where an object is either at rest (static equilibrium) or moving at a constant speed in a straight line (dynamic equilibrium), resulting in zero acceleration.
- 🔍 When solving physics problems involving equilibrium, first check if the object is in equilibrium by confirming there is no acceleration.
- 📈 Identify all forces acting on an object and represent them in a free-body diagram, which is crucial for applying Newton's laws to solve problems.
- 🧮 Apply Newton's Second Law in component form (ΣFx and ΣFy) to find the net force in each direction, which should equal zero for objects in equilibrium.
- 🤔 In equilibrium problems, the sum of the forces in the x-direction (ΣFx) and y-direction (ΣFy) must both equal zero, indicating no net force and thus no acceleration.
- 🔄 Understand the components of forces acting at an angle using trigonometric functions, such as cosine for the adjacent side and sine for the opposite side in a right triangle.
- 📝 When solving problems, you may need to solve for one force using one equation and then use that value to solve for another force in a different equation.
- 🚗 An example given was a car being towed at a steady speed with forces including weight, normal force, tension, and friction acting on it, illustrating a dynamic equilibrium scenario.
Q & A
What are Newton's three laws of motion?
-Newton's first law states that an object at rest will remain at rest, and an object in motion will remain in straight-line motion at a constant speed unless acted upon by another force. Newton's second law is mathematically formulated as F = ma, indicating the force acting on an object is equal to the mass of the object times its acceleration. Newton's third law states that every force occurs as a member of an action-reaction pair of forces, meaning for every action, there is an equal and opposite reaction.
What is meant by equilibrium in physics?
-Equilibrium refers to a state where an object is either at rest (static equilibrium) or moving in a straight line at a constant speed (dynamic equilibrium). In both cases, the object is not accelerating, which means the net force acting on it is zero.
How does Newton's second law, F = ma, relate to equilibrium?
-In the context of equilibrium, where the acceleration (a) is zero, Newton's second law simplifies to F = 0, indicating that the net force acting on an object in equilibrium is also zero.
What is the significance of a free-body diagram in solving physics problems?
-A free-body diagram is pivotal in solving physics problems as it helps to visually represent all the forces acting on an object. It is key to identifying the forces and setting up the equations correctly according to Newton's laws.
In the context of the lecture, what is the first step to solving equilibrium problems?
-The first step is to determine if the object is in equilibrium, which means checking if the object is either at rest or moving in a straight line at a constant speed, i.e., confirming that the acceleration is zero.
What is the tension in the rope if an orangutan weighing 500 newtons hangs from it?
-Since the orangutan is in static equilibrium and the only forces acting on it are its weight and the tension in the rope, the tension in the rope must be equal to the weight of the orangutan, which is 500 newtons.
In the lecture's second example, how is the tension in the rope related to the friction force opposing the car's motion?
-In the second example, the tension in the rope is found by solving the equation that includes the horizontal components of the forces. The tension in the rope is equal to the friction force (320 newtons) divided by the cosine of the angle (20 degrees), resulting in approximately 340 newtons.
What are the steps to draw a free-body diagram for the third example where a ball is held in place by two ropes at an angle?
-The steps include drawing the axes (x and y), representing the object as a dot at the center, identifying the forces (weight, two tensions), and drawing them as vectors pointing away from the dot with appropriate directions and magnitudes to reflect the equilibrium condition.
In the third example, how do you find the tension in the pulling rope (t2)?
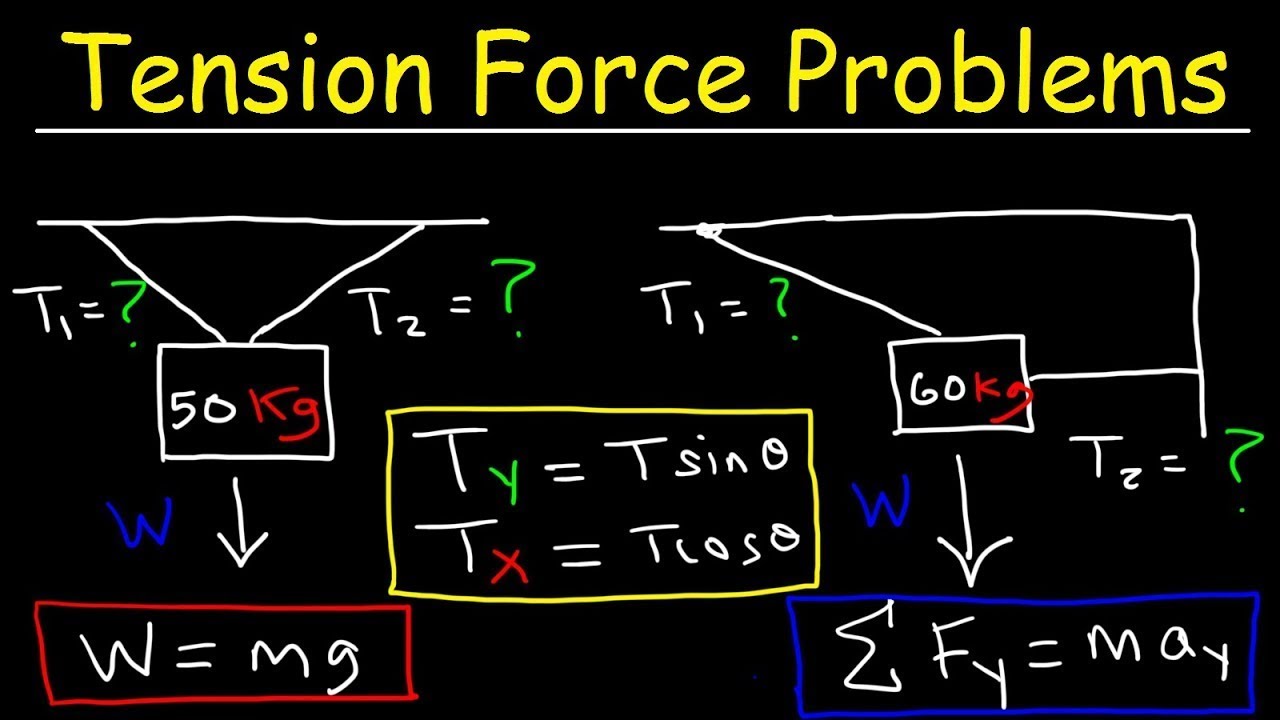
-To find the tension in the pulling rope (t2), you first solve for the tension in the other rope (t1) using the y-component equation, and then use the x-component equation to solve for t2, which involves substituting the value of t1 and the sine of the angle (20 degrees).
What is the importance of understanding angles and trigonometric functions in solving equilibrium problems with inclined forces?
-Understanding angles and trigonometric functions is crucial for breaking down inclined forces into their horizontal (x) and vertical (y) components. This allows for the correct application of Newton's second law in component form, which is necessary for solving equilibrium problems accurately.
Outlines
📚 Introduction to Newton's Laws and Equilibrium
The lecture begins with an introduction to Newton's three laws of motion. The first law, often referred to as the law of inertia, states that an object at rest will remain at rest, and an object in motion will continue in a straight line at a constant speed unless acted upon by a force. Newton's second law is mathematically expressed as F = ma, indicating the relationship between force, mass, and acceleration. The third law highlights the action-reaction force pairs, suggesting that every force has an equal and opposite reaction. The lecture's objective is to apply Newton's second law to solve problems involving equilibrium, which is defined as a state where an object is either at rest (static equilibrium) or moving at a constant speed in a straight line (dynamic equilibrium). The key takeaway is that in both cases, the acceleration is zero, leading to a net force of zero according to Newton's second law.
🔍 Problem-Solving Strategy for Equilibrium
The second paragraph outlines a step-by-step approach to solving equilibrium problems. It begins with confirming the object's state of equilibrium, which is characterized by zero acceleration. The next step involves identifying and representing all the forces acting on the object through a free-body diagram, a critical tool for visualizing the forces. The paragraph emphasizes the importance of this diagram in solving physics problems. The strategy then moves on to applying Newton's second law to these forces, particularly focusing on situations where the net force is zero due to equilibrium. The goal is to solve for unknown forces, such as tension in various scenarios, by setting up and solving equations based on the balance of forces.
🦍 Analyzing an Orangutan in Static Equilibrium
This section presents a simple example of an orangutan hanging from a vertical rope, illustrating the concept of static equilibrium. The problem involves determining the tension in the rope. The orangutan is at rest, indicating no acceleration and thus confirming equilibrium. The forces considered are the weight of the orangutan (downward force) and the tension in the rope (upward force). A free-body diagram is used to visualize these forces, with the tension and weight forces being equal in magnitude but opposite in direction. By applying Newton's second law, the net force is set to zero, leading to the conclusion that the tension in the rope equals the weight of the orangutan, which is given as 500 newtons.
🚗 Towing a Car at Steady Speed: Dynamic Equilibrium
The example of a car being towed at a steady speed introduces dynamic equilibrium, where the car is moving but not accelerating. The problem requires finding the tension in the rope that is pulling the car. The forces at play include the car's weight, normal force, tension in the rope, and friction opposing the motion. The free-body diagram is expanded to include these forces, with the tension force being broken down into its x and y components using trigonometric functions. The problem is solved by setting up two equations based on the equilibrium condition (net force equals zero) for both the x and y directions. The solution process involves algebraic manipulation to isolate and solve for the tension in the rope.
🎯 Solving for Tension with Trigonometry and Components
This paragraph delves deeper into the solution process for the car towing problem, emphasizing the need to understand the x and y components of the tension force acting at an angle. The x component of the tension force is calculated using the cosine function, while the y component uses the sine function, both in relation to the given angle of 20 degrees. The paragraph explains how to set up the equations for both components and solve for the unknown tension using the given values for friction and angle. The solution process involves algebraic manipulation and an understanding of trigonometry to find the tension in the rope, which is crucial for solving the problem.
🏀 Ball in Static Equilibrium with Multiple Forces
The final example involves a ball held in place by two ropes at an angle, adding complexity to the problem with multiple forces and angles. The ball is in static equilibrium, with no acceleration. The forces include the weight of the ball, two tensions (differentiated as T1 and T2), and the angle between the ropes and the vertical. The free-body diagram is crucial for visualizing and solving the problem. The paragraph explains how to break down the forces into their x and y components, using sine and cosine functions respectively. The problem requires solving two equations simultaneously: one for the x components and one for the y components of the forces. The solution process involves finding the values of T1 and T2, with the ultimate goal of determining the tension in the pulling rope (T2).
📘 Conclusion and Preview of Future Lectures
The lecture concludes with a summary of the problem-solving strategies and examples covered, emphasizing the importance of understanding equilibrium and Newton's laws. The speaker previews the next lecture, which will focus on solving problems involving acceleration, where equilibrium is not present. The conclusion reinforces the concepts learned and encourages students to practice these strategies for tackling more complex physics problems.
Mindmap
Keywords
💡Equilibrium
💡Newton's Laws of Motion
💡Static Equilibrium
💡Dynamic Equilibrium
💡Net Force
💡Free Body Diagram
💡Tension
💡Friction
💡Normal Force
💡Trigonometry
Highlights
Newton's first law states an object at rest will remain at rest, and an object in motion will remain in straight line motion at a constant speed unless acted on by another force.
Newton's second law is mathematically formulated as F = m*a, relating force, mass and acceleration.
Newton's third law states every force occurs as an action-reaction pair, with equal and opposite forces acting on different bodies.
The goal is to apply Newton's second law to solve problems, starting with the simplest case of equilibrium.
Equilibrium means an object is either at rest (static equilibrium) or moving at constant speed in a straight line (dynamic equilibrium).
In both static and dynamic equilibrium, the object's acceleration is zero, so the net force is also zero according to Newton's second law.
To solve equilibrium problems, first check if the object is in equilibrium with zero acceleration.
Next, identify all the forces acting on the object and draw a free body diagram.
Apply Newton's second law in component form (ΣFx = 0 and ΣFy = 0) to solve for the unknown forces.
In the orangutan example, the tension in the rope equals the orangutan's weight of 500 N since only weight and tension forces are acting.
For the car example, the tension in the rope can be found by solving the horizontal force equation ΣFx = 0, knowing the friction force and angle.
When a force is at an angle, resolve it into x and y components using trigonometry (T*cosθ for x, T*sinθ for y).
In the ball example, two tensions act on the ball. Solve the vertical force equation first to find one tension, then use it to solve the horizontal equation for the other tension.
Drawing accurate free body diagrams is crucial for writing out the correct equations to solve the problem.
This lecture focused on solving problems with objects in equilibrium. The next lecture will cover cases with non-zero acceleration.
Key steps to solving equilibrium problems: check equilibrium, identify forces and draw free body diagram, apply Newton's second law in component form.
Understanding the concept of equilibrium and how to apply Newton's laws is fundamental to solving a wide range of physics problems.
Transcripts
Browse More Related Video

Rotational Equilibrium Introduction (and Static Equilibrium too!!)

College Physics 1: Lecture 21 - Solving Circular Dynamics Problems

High School Physics - Ramps and Inclines

Newton's First Law of Motion | Newton's Laws of Motion | Video for Kids

Static and Dynamic Equilibrium
Tension Force Physics Problems
5.0 / 5 (0 votes)
Thanks for rating: