Wave Function
TLDRIn this AP Physics essentials video, Mr. Andersen explores the concept of the wave function, which is pivotal for calculating the probability of finding matter in specific areas. He creatively uses a crime wave map of Washington DC to illustrate the probabilistic nature of wave functions, drawing parallels to the behavior of electrons. The video delves into the wave-particle duality of matter, emphasizing the shift to the wave model at the quantum level. It explains the double-slit experiment, demonstrating how electrons exhibit wave-like interference patterns. The script also discusses the collapse of the wave function when measurement occurs, reverting electrons to particle-like behavior. Lastly, Mr. Andersen guides viewers on how to interpret wave functions, highlighting the importance of amplitude in determining the likelihood of finding a particle at a certain location.
Takeaways
- 🌊 The wave function is a mathematical tool used to calculate the probability of finding matter in a particular area.
- 🗺️ An analogy is made between crime waves in Washington DC and the wave function, illustrating how probabilities are shown without predicting specific events.
- 📦 Matter can be treated as both a particle and a wave, with the wave model becoming more relevant at smaller scales.
- 🌀 The wave function's absolute value is used to determine the probability of finding matter in a given location.
- 📚 In AP Physics, students must be able to interpret wave functions to understand where matter is more likely to be found.
- 🎨 The double-slit experiment with paint balls demonstrates particle-like behavior, with paint balls hitting the screen in predictable patterns.
- 💧 When water waves are used in the double-slit experiment, interference patterns emerge, showing wave-like behavior.
- ⚛️ Electrons, when used in the double-slit experiment, exhibit wave-like interference patterns, indicating their wave-like nature.
- 🔬 Observing which slit an electron goes through causes the electron to behave like a particle, demonstrating the wave-particle duality.
- 📈 The amplitude of the wave function indicates the likelihood of finding a particle at a certain location, with higher amplitudes corresponding to higher probabilities.
- 📚 The script emphasizes the importance of being able to read and interpret graphical wave functions to understand the behavior of matter waves.
Q & A
What is a wave function and why is it important in quantum physics?
-A wave function is a mathematical description used in quantum mechanics to calculate the probability of finding a particle, such as an electron, in a particular location. It is important because it helps us understand the behavior of matter at the quantum level, where classical physics no longer applies.
How does the concept of a 'crime wave' relate to the wave function in the context of the video?
-The 'crime wave' analogy is used to illustrate how probabilities work in a real-world context. Just as a crime wave map shows areas with a higher probability of crimes without predicting specific incidents, the wave function shows areas with a higher probability of finding particles without pinpointing their exact location.
What is the significance of treating matter as both a particle and a wave?
-Treating matter as both a particle and a wave is significant because it reflects the dual nature of quantum objects. At larger scales, objects behave more like particles, but at the quantum level, they exhibit wave-like properties, such as interference, which is crucial for understanding phenomena like electron behavior.
How does the wave function model differ from the particle model in terms of locating matter?
-The particle model suggests that a particle can be in a specific location within a box, and if it's in one place, it can't be in another. In contrast, the wave function model provides a probability distribution, indicating regions where particles are more likely to be found rather than exact positions.
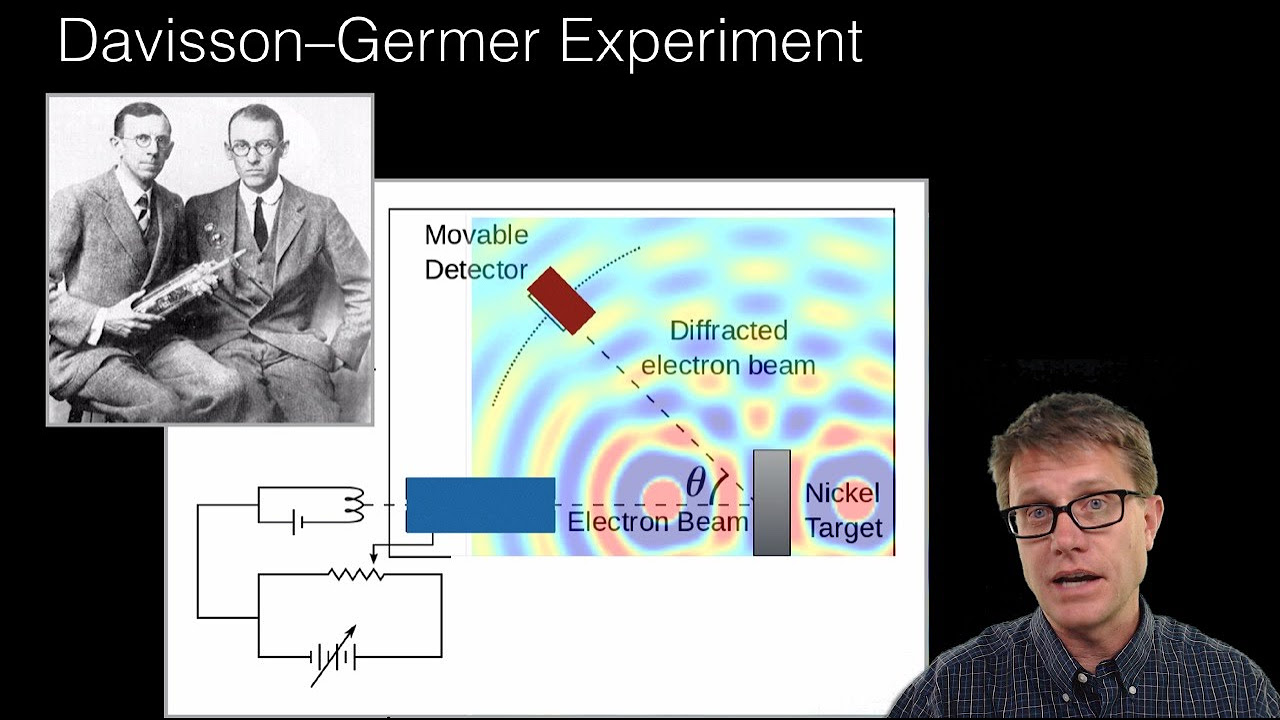
What is the double-slit experiment, and what does it demonstrate about the nature of electrons?
-The double-slit experiment is a classic physics experiment where a beam of particles (or waves) passes through two slits, creating an interference pattern on a screen. It demonstrates that electrons, and other quantum particles, can exhibit wave-like interference patterns, suggesting they have properties of both particles and waves.
How do the interference patterns observed in the double-slit experiment with electrons differ from those expected with paint balls?
-With paint balls, which behave as particles, the distribution on the screen would be two distinct clusters corresponding to the two slits. However, with electrons, an interference pattern emerges, with areas of constructive and destructive interference, indicating wave-like behavior.
What happens when an observer tries to determine which slit an electron passes through in the double-slit experiment?
-When an attempt is made to observe which slit the electron passes through, the interference pattern disappears, and the electrons behave like particles again, creating two distinct clusters on the screen. This is known as the collapse of the wave function due to observation.
How does the amplitude of a wave function relate to the probability of finding a particle?
-The amplitude of a wave function is directly related to the probability of finding a particle. Areas with a higher amplitude indicate a higher probability of finding the particle, while areas with a lower amplitude indicate a lower probability.
What is the significance of the wave function's highest amplitude in determining the location of a particle?
-The highest amplitude of a wave function signifies the location with the greatest probability of finding the particle. It is the peak of the probability distribution, indicating where the particle is most likely to be detected.
How can one read and interpret a wave function graph to determine the likelihood of finding a particle at different locations?
-To interpret a wave function graph, one should look for the points of highest amplitude, as these indicate the areas with the highest probability of finding the particle. The shape and peaks of the graph provide a visual representation of the probability distribution.
What is the role of amplitude in determining the probability of finding a particle represented by two different wave functions?
-When comparing two wave functions representing different particles, the amplitude of each function indicates the relative probability of finding each particle at various locations. The wave function with the higher amplitude at a given location suggests a greater likelihood of finding the particle there.
Outlines
🌊 Wave Function and Matter Probability
Mr. Andersen introduces the concept of the wave function in quantum physics, explaining its use in calculating the probability of finding matter in certain areas. He uses the analogy of a crime wave map to illustrate how probability is represented. The video then transitions into a discussion of how electrons can be treated as both particles and waves, emphasizing the shift to the wave model at smaller scales. The concept of a particle in a box is contrasted with the wave function, which is necessary to calculate probabilities. The video script also introduces the double-slit experiment to demonstrate the wave-like behavior of electrons, including interference patterns and the act of measurement affecting their behavior.
Mindmap
Keywords
💡Wave Function
💡Probability
💡Particle
💡Wave
💡Wave-Particle Duality
💡Double Slit Experiment
💡Interference
💡Amplitude
💡Quantum Mechanics
💡Observation
Highlights
Wave function is used to calculate the probability of finding matter in specific areas.
Crime wave analogy used to explain the concept of probability in wave function.
Matter can be treated as both a particle and a wave, with a shift to the wave model at smaller scales.
Wave function requires a complex calculation to determine the probability of finding matter.
Absolute value of the wave function is used to show the probability of matter's location.
Understanding wave functions is essential for AP Physics, particularly in reading and interpreting them.
Double-slit experiment demonstrates the difference between particle and wave behavior.
Paint balls behave as particles, distributing on a screen in a predictable pattern.
Water waves interfere with themselves, creating areas of high amplitude and cancellation.
Electrons, when used in the double-slit experiment, exhibit wave-like interference patterns.
Electrons interfere with both past and future electrons, demonstrating a non-intuitive wave property.
Observing which slit an electron passes through causes them to behave like particles, not waves.
Wave function is confounding and cannot be directly measured.
Wave function amplitude indicates the likelihood of finding a particle at a certain location.
Graphical wave functions can be used to qualitatively determine where matter waves are likely to be found.
Highest amplitude in a wave function corresponds to the highest probability of finding the particle.
The video aims to teach viewers how to use graphical wave functions for determining the location of matter.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: